类比的形似与神似

类比的形似与神似——从平面几何到立体几何

刘　燃

类比是研究数学的一种重要方法，通过两类具有相似特征的现象之间的对比，从一类现象的某些已知特征推测另一类现象相似特征的存在。类比是提出问题并作出新发现的主要源泉，是科学研究最具普遍性的方法。当然用类比法得出的命题不一定正确，还要经过严格的证明。现就笔者的一节公开课从平面几何到立体几何的对比来研究类比与论证。

一、类比的引出

本学期笔者的教学走进了立体几何的范畴，对空间想象能力和论证推理能力有所侧重。例如立体几何中有这样一个命题“正四面体内一点到正四面体四个面距离之和为定值”，许多人一看到它一筹莫展，全没思路。但在平面几何里这样一个命题“等边三角形内的任意一点到三角形的三边的距离之和等于常数”相信一定不难解决，由于平面几何中该命题的证明可采用“面积法”，类似地，这个立体几何问题应采用“体积法”，于是问题迎刃而解，难就难在如何引导他们学会建立类比，架起一座从二维空间到三维空间的桥梁。

首先在这节课的设计上，在引入部分笔者设计了这样两个问题：

1.到两定点距离相等的点的集合是什么？

2.到三角形三顶点距离相等的点的集合是什么？

由于思维定式，学生一定会按照平面几何框架分别回答是中垂线和外心，于是陷阱成功，随着模型的出现，相信他们不难理解在立体几何中答案分别是两点连线的中垂面和过外心且垂直于三角形所在平面的直线。接着不妨引导学生自己得出结论“随着我们观察角度从两维空间到三维空间，我们所研究对象具有的性质发生变化：从点到线（外心——过外心且垂直于三角形所在平面的直线），从线到面（中垂线——中垂面）”。在此我们仅做出了类比猜测结论，而并未进行论证，简单的模型代替了证明，但同时要指出绝对的照搬会出错，故而需要论证。

二、类比的载体

由于类比思维的认识依据是事物之间具有相似性，所以我还设计了这样一个过程——请他们找出一些与平面多边形有相似特征的立体多面体，把这两类具有相似特征的现象作为载体，以便从中类比。事实证明学生对这一过程充满兴趣，而兴趣才是最好的老师。类比需要热情的联想，论证需要冷静的理智，但是必须先有前者。同时这一部分将为我们下面的研究载体埋下伏笔。

师：在平面几何中的一些图形，如正方形、长方形、三角形、正三角形、直角三角形等，在立体几何中我们能否找到与之类似的几何体呢？

生：正方体、长方体、四面体、正四面体，直四面体……（有同学认为三角形对应三棱锥，教师当场指出三棱锥即四面体，而正三角形对应正四面体更确切，直四面体为使用方便易当即给出描述定义）。

三、类比的形似

在师生共同探究问题部分笔者又设计了两组问题：

1.从边长到面积

平面几何：Rt△ABC中，∠BAC＝90°，AD⊥BC，D是垂足，则有AB²＝BD·BC

立体几何：直四面体V　ABC中，棱VA、VB、VC两两垂直，VO⊥面ABC，O是垂足，则有什么结论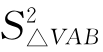？（＝S△AOB·S△ABC）

这里我们可以看出问题的载体是形似的，从直角三角形到直四面体，垂直关系的延续，直角顶点在斜边的垂足变形成直角面在斜面的射影，所以单纯就猜想来说这个结论不难类比。边长到面积似乎也迎合开篇的从线到面，继续伏笔。

2.从面积到体积

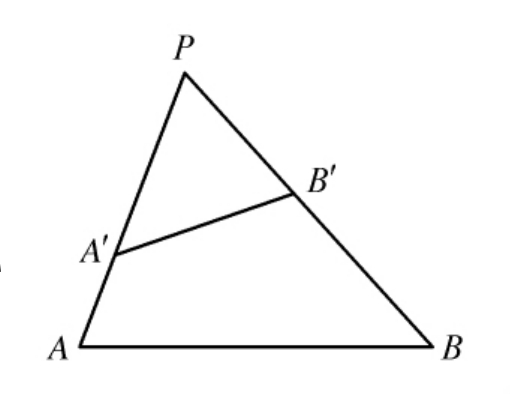
平面几何：任意△PAB被一直线截边PA、PB于A′、B′点，则有什么结论？

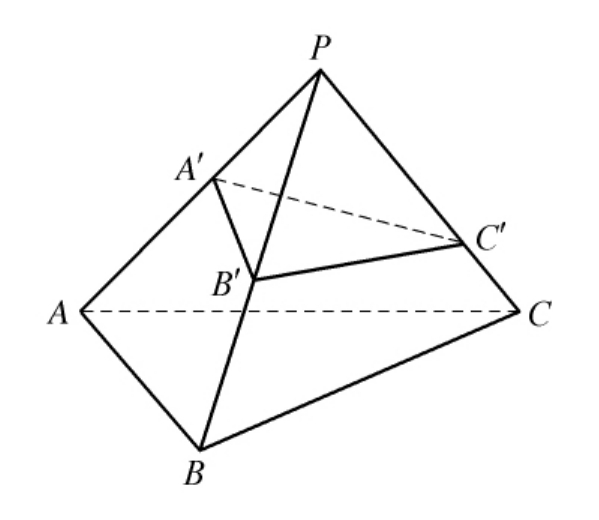
立体几何：任意三棱锥P　ABC被一平面截棱PA、PB、PC于A′、B′、C′点，则有什么结论？

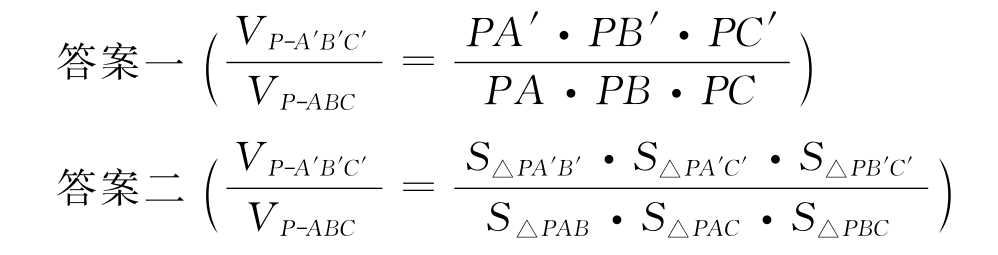
载体是相似的，答案二错误也是意料之中的。延续了从边长到面积，不难猜想是面积到体积的类比。等式左边面积比转化为体积比，等式右边边长相乘极易变为面积相乘之比，但绝对的照搬失去类比的意义必然造成谬论。

四、类比的神似

在这两组问题上，我采用的方式基本上都是给出载体，请他们小组讨论猜测命题结论，最后完成证明过程。第一组问题结论基本没有争议，在方法上有区别，尤其要指出的是我们除了形似还要做到神似，这就是解决问题的方法之类比。

给出“Rt△ABC，∠BAC＝90°，AD⊥BC，D为垂足，则有AB²＝BD·BC”的简单证明：∵cos　B＝BD∶AB＝AB∶BC　∴AB²＝BD·BC

不难推出：设二面角V-AB-C大小为θ，则cosθ＝S_△AOB∶S_△VAB＝S_△VAB∶S_△ABC那么（S_△VAB）²＝S_△AOB·S_△ABC，此处我们还可以将平面角类比到二面角。

从面积到体积这组题目的解决方法同样对第二组问题起一个基石作用。

在分析从面积到体积错误答案二时需要强调三点：

1.类比法得出的命题不一定正确，还要经过严格的证明。

2.不仅在形式上可类比，而且在证明方法上也可以类比。

3.平面几何到立体几何的类比不是绝对的照搬“从点到线、从线到面”。

数学家G·波利亚说：“类比是一个伟大的引路人。”在数学的教学与研究中，类比是进行合情推理的一种非常重要的思维方法。当两个对象系统中某些对象间的关系存在相似性时，我们便可对这两个对象系统进行类比，从而可以从一个对象系统得到的某些结果去猜测和发现另一系统的相应的新结果。同样我们分析问题解决问题的过程中则可以利用一个较简单的类比问题的解答方法或结果，去找到原问题的解决方法。

本节课让学生自主地从平面几何提炼命题到立体几何，融会已有的知识来解决新的问题或发现新的规律等，可以激发学生的学习热情。在探究过程中，通过教师与学生、学生之间的讨论和交流，体验类比论证的实施过程，加深了类比思维的理解，为学生今后的深入学习从思维方式层面进行铺垫，致力于提升学生的学习能力。在全民意识到“创新是一个民族乃至一个国家的灵魂”的时候，培养学生的创新意识和创新能力，是我们一线教师刻不容缓的任务。教师必须不断更新教育观念，完善教育方法，开发学生潜能，为培养具有创新精神的高素质人才而努力。