提高解题效率

培养观察能力　提高解题效率

杨成功

（略阳天津高级中学，陕西　略阳　724300）

【摘要】观察是数学解题教学的一项基本任务，是新课标的基本要求，如何培养观察能力，关键在于数学中激发观察的兴趣和动力，教给学生观察方法和技巧。

【关键词】观察　解题　效率

观察是人们认识事物最基本的途径，是发现问题、解决问题的前提。解每一道数学题，都应从观察入手，边看边想，从观察中寻求解题思路，产生联想，发现解题捷径，从而展开创造性思维。因此，引导学生掌握观察方法，培养观察能力，是数学教学的一项基本任务，也是新课标的基本要求。笔者结合平时教学中的做法，谈谈自己的体会。

一、结合学生的认知阶段，激发观察的兴趣和动力，培养观察能力

学生在认知过程中，教师要想方设法，有意识、有目的地引导他们正确地运用科学方法去认识事物、感知知识，使他们能在复杂的事实中，发现其细微的变化及特征，使其进一步上升为理性认识。例如，在学习指数函数与对数函数时，学生对这两个函数的单调性容易搞混淆，这时教师可引导学生观察教科书上的图表，发现指数函数y=a^x，当a＞1时，图像随着x的增大而逐渐呈上升趋势（即y随x的增大而增大），当0＜a＜1时，图像随着x的增大而逐渐呈下降趋势（即y随着x的增大而减小）。由此启发学生总结归纳出：指数函数y=a^x，当时a＞1，图像是一撇（递增），当0＜a＜1时，图像是一捺（递减）。此时，学生顿时豁然开朗，在大脑里对其单调性有了深刻的认识。于是，教师不失时机地再引导学生对对数函数图像进行观察发现并归纳结论：当a＞1时，函数y=log_ax的图像随x的增大而逐渐呈上升趋势（递增），当0＜a＜1时，图像随x的增大而逐渐呈下降趋势（递减）。至此，再引导学生将指数函数图像、对数函数图像a＞1与0＜a＜1各画在同一坐标系内进行观察比较发现：当a＞1时，它们同为增函数，当0＜a＜1时，同为减函数，其定义域不同（指数函数x∈R，对数函数x＞0）。通过一番观察、比较，学生很快对这两种函数的图像及单调性了如指掌。

有些学生在观察时，缺乏毅力，马马虎虎；有的只是凭一时兴趣，观察抓不住重点；有的只是局部观察，导致观察不全面……这些问题，不同程度地阻碍了学生在认识上的深化。为此，教师在教学中必须教育他们观察时要仔细认真并有目的地围绕一个中心去观察，同时要求做到在观察中思考，思考中观察。只有这样才能在观察中培养思维的品质。

二、结合数学解题教学，教给学生观察的方法和技巧，培养观察的品质

众所周知，观察是解题过程中一种重要的思维活动。如果在解题时对题目的数与形有意识地进行观察、分析，常常会产生意想不到的惊喜。教师在指导学生解题时，可以抓住以下几个方面进行，以收到实效。

（一）观察时要引导学生注意题目的特点（特征）

善于抓住事物的特点或特征，是认识事物本质的关键。有些数学题目具有本身的特点或数字特征，若能及时抓住，则能起到事半功倍之效果。例如，“设9cosA+3sinB+tanC=0，sin²B－4cosA·tanC=0，求证：|cosA|≤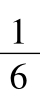”。初看本题，不好下手，教师可引导学生观察两个条件的结构特点，发现如果把第一个条件看成是3的二次方程，那么第二个条件即为前者的判别式△=0形式。由此可令x=3，则x²cosA+xsinB+tanC=0，若cosA=0，则所证不等式成立；若cosA≠0

∵sin²B－4cosA·tanC=0，∴上述方程有两等根x₁=x₂=3，于是9=x₁x₂=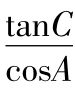即tanC=9cosC，从而36cos²A=sin²B≤1，故|cosA|≤.

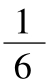（二）观察时要引导学生观察内在规律

有些题目看似无章可循，其实存在着内在的本质规律，如不认真地进行观察，很难揭开神秘面纱。

如“求1·2+2·3+3·4+…+n·（n+1）的和.”注意并联想其差式：

k（k+1）（k+2）－（k－1）k（k+1）=2k（k+1）

即可使我们想到若用1，2，…n代替上式中的k可得：

1·2·3－0·1·2=3·1·2

2·3·4－1·2·3=3·2·3

………………

n·（n+1）·（n+2）－（n－1）·n·（n+1）=3·n·（n+1）

上述各式相加得：

n（n+1）（n+2）=3·［1·2+2·3+3·4+…+n（n+1）］=3·S_n.

∴S_n=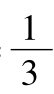n（n+1）（n+2）.

再如证明：（1+tan1⁰）（1+tan2⁰）（1+tan3⁰）…（1+tan44⁰）=2²².观察等式特点及数字规律，发现：（1+tan1⁰）（1+ tan44⁰）=1+tan1⁰+1+tan44⁰+1+tan1⁰·1+tan44⁰.联想到和角的正切公式变形：tanα+tanβ=tan（α+β）（1－tanαtanβ）

∴（1+tan1⁰）（1+tan44⁰）=1+tan（1⁰+44⁰）（1－tan1⁰tan44⁰）+tan1⁰tan44⁰=2.

同理（1+tan2⁰）（1+tan43⁰）=2…（1+tan22⁰）（1+tan23⁰）=2.

∴原式左端=2²²故等式成立。

发现内在规律，似如鱼得水，突现思维的飞跃，彰显解题风采，观察之壮举。

（三）引导学生观察时注意把握题目的隐含条件

所谓隐含条件，是指若隐若现，含蓄不露的已知条件。教学中时常发现学生因不能挖掘隐含条件而使思维受阻，不能完成解题。教师应在此时引导学生展开联想，挖掘隐含条件，掌握数值关系，理清已知与未知之间的关系。从而，在观察中培养学生思维的灵活性、准确性、深刻性。如：“已知实系数二次方程x²+2ax+b=0的两根分别为直角三角形两锐角的余弦值，问a，b应满足什么条件？”这道题常见错误是忽视△≥0这一条件，从而导致得出的a，b关系式错误。

教师可引导学生这样观察、分析、思维：

设直角三角形两锐角分别为A，B.则A+B=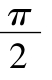　　　　 ①

cosA＞0，cosB＞0②

根据韦达定理得：cosA+cosB=－2a　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　③

　　　　　　　　cosAcosB=b　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　④

又△=4a²－4b≥0　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　⑤

由①知：B=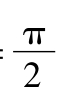－A代入③，④，得

cosA+sinA=－2a，cosAsinA=b

∴4a²－2b=1　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　⑥

又由②，③，④，知a＜0，b＞0由⑤，⑥，知b＜.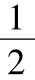

∴a，b应满足的关系式为a=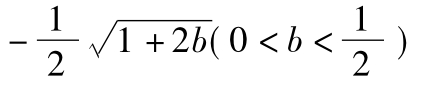

若忽视△≥0这一条件，则误认为4a²－2b=1为所找a，b关系。

（四）引导学生立足整体，全面观察

观察要从不同的角度，全方位地进行观察，从而把握问题的全貌。通过观察问题的整体，抓住它的特征，及各个组成部分之间的关系，往往能“柳暗花明”，甚至“绝处逢生”。

例如，设对所有实数，不等式

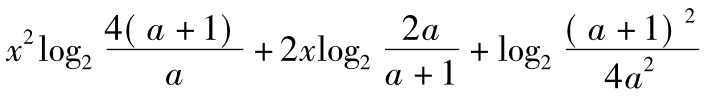＞0恒成立，求a的取值范围。

教师引导学生整体观察不等式的结构，发现不等式左边三项中的对数可以化为同一形式，从而原不等式可以化简：

将原不等式变形得，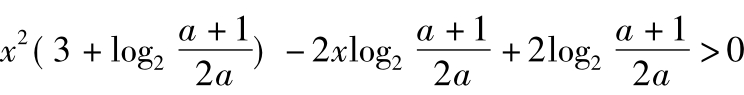

即3x²+（x²－2x+2）×log₂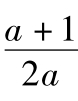＞0.∵x²－2x+2=（x－1）²+1＞0，

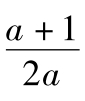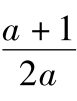∴原不等式恒成立的充要条件为log₂＞0，即＞1.

故a的取值范围是0＜a＜1.

虽然也可以从二次函数角度转化为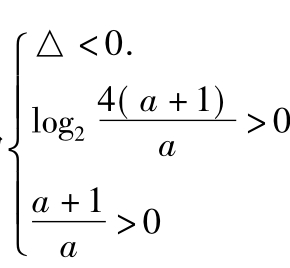，但运算量大，且十分繁琐。

值得注意的是：学生在由感性认识上升为理性认识的同时，教师应不失时机地教育学生养成良好的观察习惯，自觉地进行观察。拿到题目，由观察数式联想到形，由形想到数；由静到动，由动止静：由表及里，由浅入深。当然，一个人的观察能力不是一朝一夕就能培养起来的。这就要求学生在学习数学时，要经常锻炼观察的毅力，使其与数学思想和数学方法形成有机的整体，从而促进数学素养的提高，为数学解题打下坚实基础。

参考文献

［1］刘学平.解题教学中观察能力的培养［J］.中学数学教学参考，1998.

［2］梁法驯.数学解题方法［M］.武汉：华中理工大学出版社，1995.

［3］李俊秀.数学教育学概论［M］.北京：地震出版社，1989.

［4］单文海，等.中学数学解题思想方法技巧（高中）［M］.西安：陕西师范大学出版社，2006.