无理数地位的初步确立

我们已经看到，无理数的出现在东西方产生了完全不同的影响。在东方，如在我国，并没有把无理数的出现当作什么大事，这在以实用计算为主的背景下是很自然的事。至于对无理数是否是数这一问题，在我国古代根本就没有人去认真考虑。但在西方由于数学背景的不同，无理数是否可以看作是数一直受到置疑。事实上，无理数作为数的地位的确立在西方经历了很长的时间。

在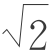的无理性被发现后，施乐尼的泰奥多勒斯又证明了、也都具有这种无理性，即它们都不可能是整数或整数的比。更多这类新数的出现，导致了越来越大的问题。后来，正如我们前面已提到的欧多克索斯提出的解决方案圆满地解决了这一课题。然而，我们也提到了，他的理论是通过几何方法解决的，所以无理数是不是数仍然待定。

虽说在古希腊，人们出于理论的考虑不愿意明确承认无理数是数，但出于实际计算的需要，数学家们却不得不用近似值来表示它们。如毕达哥拉斯学派先用49／25代替2，然后得出≈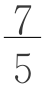。泰奥多勒斯先用49／16代替3，然后求出。还有人使用过其他的求近似值的方法。不晚于公元前四世纪，希腊数学家们还熟知了一种求平方根的近似方法。这种方法相当于连分数法。许多数学家计算中用到了无理数的近似值，这一定程度上促进了无理数作为数的地位的确立。

到1500年左右，西方人对无理数用得更加随便了。许多人都按照印度人和阿拉伯人的传统使用无理数，并引入种类越来越多的无理数，例如，史提菲使用了这种形式的无理数。卡尔达诺曾把含立方根的分数有理化。使用无理数的广泛程度，从韦达的表示π的式子就可以看出来。

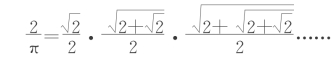
虽然如此，但对于无理数是否确实是数却仍有不同的看法。很多数学家对无理数表示出一种矛盾的心理。他们一方面随意使用无理数进行各种计算，另一方面却怀疑它们的意义和存在的真实性。德国数学家史提菲在他的重要著作《整数算术》这一部论述算术、欧几里得《几何原本》第十篇无理数以及代数的书中，讨论了用十进制小数的记号表达无理数的问题。他的典型说法反映了许多数学家对待无理数的矛盾态度。

他一方面说：“在证明几何图形的问题中，由于当有理数不行而代之以无理数时，就能完全证出有理数所不能证明的结果……因此我们感到不能不承认它们确实是数，迫使我们承认的是由于使用它们而得出的结果——那是我们认为真实、可靠而且恒定的结果。但从另一方面讲，别的考虑却迫使我们不承认无理数是什么数，例如，当我们想把它们数出来（用十进制小数表示）时，……就发现它们无止境地往远跑，因而没有一个无理数实质上是能被我们准确掌握住的……，而本身缺乏准确性的东西就不能称其为真正的数……所以，正如无穷大的数并非数一样，无理数也不是一个真正的数，而是隐藏在一种无穷迷雾后面的东西。”

他接着论证说实数不外乎整数或分数；无理数显然既非整数又非分数，因而不是实数。

不把无理数看作是真正的数，而是把它当作一种依附于几何量的形式上的符号的观点，在很晚的时代仍然在许多数学家中非常流行。

无理数究竟是一个真正的数，还是一个离不开几何量的形式上的符号？在这个问题上，无理数的支持者与旧观念的维护者展开了长期的论战。

18世纪之前，大部分数学家对无理数持否定态度。帕斯卡和巴罗说，像这样的数只能作为几何上的量来理解；无理数仅仅是记号，它们脱离连续的几何量便不能存在，而对无理数进行运算，要以欧几里得关于量的理论来作逻辑依据。牛顿在他的《普遍的算术》中也持这一观点。

只有少数一些人则肯定说无理数是独立存在的东西，斯蒂文承认无理数是数，并用有理数来不断逼近它们；沃利斯在《代数》中也承认无理数是地地道道的数。笛卡尔在《指导思想的法则》（约1628年）中承认无理数是能够代表连续量的抽象的数。

到18世纪时，在弄清楚无理数概念方面仍然没有什么大的突破，但是对无理数本身作出了某些进展。如1761年兰伯特向柏林科学院提交论文，证明了π是无理数。同时，随着数学研究的深入，有更多的无理数陆续发现。虽说无理数地位的最终确立是19世纪下半叶的事，但我们将看到，无理数家族家丁兴旺的景象毕竟使得无理数的支持率大幅度上升了。