化归意识的培养

第三节　化归意识的培养

把尚未解决或难以解决的问题，通过适当的转化，逐步归结为一类已经解决或易于解决的问题，从而使原来问题最终获解，这种思想方法称为化归法。经常运用此法处理数学问题的意识，称为化归意识。

一、联系与转化——实现化归的条件

数学对象常从一种状态转化为另一种状态，从一种形式转化为另一种形式。事物间的相互联系是实现转化的条件。数学问题解决的过程，是师生通过共同努力，实现转化的过程。这个过程的主要特征是：从未知向已知转化；从新知识向旧知识转化；从复杂向简单转化。只要找出了联系，就确定了转化的可能性，只要找到转化的途径，则问题解决就有可能得以实现。

1.中学数学的转化思想内涵丰富

转化，是一系列数学思想的总称，在中学数学范围内，转化包含了丰富的内容。

（1）换元思想

通过换元法，可实现从超越方程向代数方程转化，从无理方程向有理方程转化，从复合函数向简单函数转化。

（2）参数思想

通过设立适当的参数，可把多元问题转化为一元问题。利用参数，可以刻画事物的变化状态，揭示变化因素之间的内在联系。

（3）降维思想

通过截面，可把三维问题降低为二维问题。类似的思想还表现为在解方程时，从高次方程向低次方程转化，把多元函数问题转化为一元函数问题，把倍角三角函数转化为单角三角函数，把多重积分变成单变量定积分，等等。

（4）坐标思想

通过建立平面直角坐标系，可把几何问题转化为代数问题。或借助于几何图形的性质，研究有关代数或函数问题。

（5）建模思想

通过问题的特定信息，确定某种特定的映射关系，从而建立适当的数学模型把实际问题转化为数学问题予以解决。

综上所述，转化是一系列数学思想的总称，并且含有十分丰富的具体内容。

2.转化是中学数学内、外联系的体现

数学中大量的公式、定理，揭示了所研究的数学对象间的关系。数学也以其形式化的语言，描述自然科学、社会科学及技术科学的有关规律，这就为把其他学科问题转化为数学问题，也为不同领域的数学问题之间的相互转化，创设了有利条件。

用数学方法探讨物理、化学、生物、教育和工程技术问题，是数学与其他学科相互联系的体现。同样，数学内部的联系和转化是十分普遍的。

代数中的基本运算在转化思想指导下得到高层次的统一，加减法在代数和的意义下统一为加法，乘除法在积的意义下统一为乘法，通过指数概念的扩充，可把根式的乘、除、乘方、开方等运算统一为幂的指数的加、乘运算，利用复数的指数形式，可以把复数的乘、除、乘方运算，转化为幂的运算，等等。

事实上，中学数学每章、每节乃至每个课时的教学，都离不开转化。只要教师在教学中引导学生明确转化的目的，弄清转化的意义，寻找转化的条件，就能促进问题的解决，同时，学生的化归意识也能得到健康发展。

3.把握联系，打好化归的坚实基础

数学问题解决过程，是一个寻找联系、探索途径的过程，而且解决同一个问题，也有不同的途径和思路。熟悉数学的各种联系，能给运用化归方法打下坚实的基础。这也是培养解决问题能力的必由之路。在数学教学中，教师应该帮助学生探索不同数学课题之间的相互影响和联系，以及这些联系在问题解决中的应用。

学生应该能够：

①识别同一概念的等价表示，例如“直线l⊥平面M”与“直线l垂直于平面M内的两条相交的直线”是等价的。

②阐述一种表示的等价表示方法。例如，一个复数，可以用代数形式a＋bi表示，可以用三角形式r（cosθ＋isinθ）表示，可以用向量形式表示，还可以用指数形式表示，等等。

③应用和评价数学课题之间的联系，例如，哥尼斯堡七桥问题就和一笔画投递路线问题有紧密联系。

④应用和评价数学和其它学科之间的联系。能够在同一实际问题或同一数学概念的不同表示法之间找到联系。如果学生能应用这些联系实现转化，那么，他们就会同时获得得强有力的、灵活的解题工具，并能深刻地体会数学的和谐与优美。

二、学会联想与想象，寻找化归的通途

当遇到一个具有挑战性的数学问题时，有些学生只会根据题意进行一些肤浅的变换，有时在原地兜兜转转，显得漫无目的；有时越走越远，甚至走进死胡同。其中一个原因就是解题方向不明，陷入变换的盲目性。

1.定向化是化归的基本策略

数学中的转化是多样的，一般地说，在解决问题时，要向题设要求的方向，即求证或求解的方向转化，也常常会向适应于个人认识水平的方向转化。事实上，数学所研究的转化，往往是从高级到低级，从未知向已知，从复杂向简单转化，并把新的认知问题转化为某个原有的认知问题。

例如，通过作辅助线，可把多边形问题转化为三角形问题，通过分离虚部和实部，把复数问题转化为实数问题，借助于对数与指数的深刻联系，把对数问题转化为指数问题予以解决，等等。

有时，为了问题解决的需要，数学问题也会向相反方向转化，如由低维化为高维，由简单化为复杂，由特殊化为一般，等等。总之，转化的方向要视解题目标而确定。

2.联想能展开化归的通途

解决问题的过程，是从已知条件向求证（解）结果寻求联系的过程，并力求找出由条件到结果之间的推理链，由于数学的联系纵横交错，故推理链中每个环节之间的联系也不是唯一的。因而造成了解题途径的多样性，也造成了一些歧异，无效的支叉路径。

通过联想，能不断调动解题者原有认知结构中的联系。从中选择有效的联系，达到化归的目的。

3.想象有助于突破化归的难点

尽管数学中存在诸多的联系，但要从中抽取解决问题所需要的联系，有时并非易事。如能根据题目条件，对原有已掌握的知识进行适当的选择，变换、重组，通过适当合理的想象，构造出解决问题所需要的数学模型，如构造图形、构造函数、构造方程、构造数列、构靠反例，等等，这样，原有问题转化为一个新的，具体的问题，并使解题者有能力予以解决。

三、从特殊化入手，获取化归的启示

当某个问题不易获解时，我们可以转而研究相对较为容易解决的特殊情况。通过特殊化，我们容易猜测有待寻找的结论；通过特殊化，也容易探索解题的思路与方向。例如，寻求符合某种条件的点的轨迹，我们可以从对某些特殊点的探索开始，从而寻找符合条件的动点所满足的某些规律性。这是求轨迹（方程）的常用方法。

1.特殊化有助于寻找一般性结论

考虑尚待研究的对象的一些简单特例，这些特例的性质较容易寻找，而这些性质，也许就是原问题要寻找的一般性结论。一般性寓于特殊性之中，有时就是这个道理。

2.特殊化有助于寻求解题思路

有些问题，情景较复杂，造成计算量大，或要考虑的情况较多。此时可退到特殊、简单的情况，从特殊情况中寻求解答方法，再回到原问题中求解，这是解决问题常用的以退为进的策略。

3.利用特殊结构，引起特殊联想

在教学中，有时要引导学生把注意力倾注在对象的某些特殊方面，由特殊结构引起特殊联想，从而找到解题途径。

4.先找一般规律，再解特殊问题

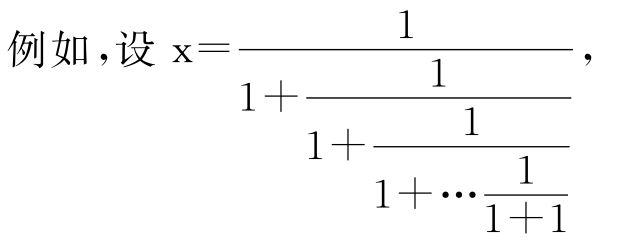
已知上式有1999条水平分数线，问x²＋x＞1是否成立？

分析：本题宜从一般情况入手，寻找一般规律，再解决题设的特殊问题。

解：令x_n表示有n条水平分数线的，形如x的分数，则有一般的递推关系

易求得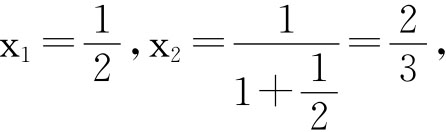

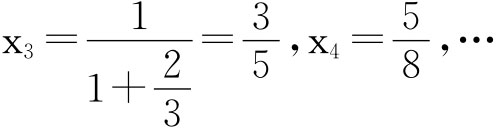
记y_n＝x_n²－x_n，我们研究y_n＋1－1和y_n－1的关系。

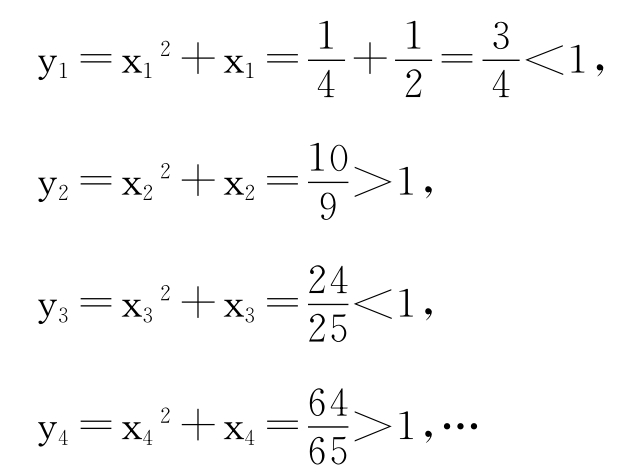
根据以上特例，我们猜测：

当n为奇数时，y_n＜1；当n为偶时，y_n＞1。当猜测成立时，我们回到上面的特殊情况，即有y₁₉₉₉＜1，从而有1999条水平分数线时，x²＋x＞1不成立。具体证明请读者自证。

四、在解决问题中锻炼，提高化归能力

通过解题学习解题，是提高化归能力的重要途径。在解题教学中，教师要引导学生在实践中演练、感知、体会化归的思想方法，逐步形成一系列行之有效的解题策略。如化繁为简，化生为熟，化整为零，化曲为直，以形论数，以数论形，等等，在遇到新的问题情景时，能以有效的思维策略，去探索转化的途径。

在化归过程中，学生由于思维的片面性，或由于原有知识基础不够扎实，产生诸多错误，或以特殊代替一般，或者忽视特殊情况，或者忘记重要的定理公式，或者产生概念的混淆，等等。

在数学教学中，教师要注意纠正上述错误，引导学生查找错误原因，从而提高学生的辨析能力，培养良好的思维品质。以下简要介绍学生在解决问题时的常见错误，以供防错纠错参考。

1.基础不牢，思路受阻

问题解决的思路，可以比喻为一条推理链，其中每个环节联系着不同的知识和方法，如果其中一个环节的相关知识（或方法）在解题者的头脑中找不到应有的位置，则称为知识（或方法）遗忘，只有调动记忆，把所需的知识（或方法）检索出来，解题过程才能继续进行。

即使解题者具备所需要的知识，但是，面对不熟悉的问题情景，有时在某一环节上未能找到条件和所求的联系，因而思维过程未能按预想方向进行，或因化归变形不当，使解题过程陷入复杂局面，这就称为思路受阻。

无论知识遗忘或者思路受阻，都是解题者知识不牢，方法不熟练的表现，因此，抓好基础知识、基本数学思想方法的教学，是解题过程得以顺利进行的先决条件。

2.审题不周，遗漏信息

正确理解题意，全面掌握已知条件和设问要求，是问题解决的奠基性工作，然而，不少学生由于审题不周，或忽视部分条件。或误解题意，致使后面所做的化归工作成为无效劳动。

2.概念不清，判断失真

数学是由众多概念、定理构成的网络体系，已知的概念和定理是推理的根据，化归的基础，如果学生对有关的概念、定理未弄清楚，必然导致判断、推理或计算的错误，从而使所进行的化归也失去意义。

3.分类不当，顾此失彼

有些概念需要分类定义，有些问题需要分情况讨论，如果情况辨别不清，忽视恰当分类，必然造成顾此失彼，从而犯以偏概全的错误。

4.忽视范围，换元失效

换元法是化归的具体方法之一，在研究方程、函数时广泛使用。学生在使用换元法解决有关问题时，如果不注意所换字母范围的变化，将会造成换元的失效。

为了引导学生正确进行化归，纠正类似上述所指出的错误，在教学中要帮助学生形成以下良好的学习习惯：

①认真审题，全面收集解题信息；

②重视分类，注意等价转化；

③正确处理特殊与一般的关系。