主成分的求解原理

6.1.4　主成分的求解原理^＊

前一节介绍了主成分分析的基本步骤。为什么对协方差矩阵Z进行特征分解就可以确定新的坐标系（主成分轴、载荷轴）和新变量（主成分得分）呢？本节对其原理进行介绍。

设p维空间的向量x的线性组合构成一个新的综合变量为

为了用尽可能少的综合变量替代原变量，就要求每个新变量尽可能多地集中所有原变量的信息，这可以由新变量的方差来表达，亦即方差var（f₁）越大，变量f₁所包含的信息量越多。显然对任何常数k，都有

亦即向量a₁乘以一个常数后，可使方差var（f₁）任意增大，要使方差var（f₁）可以比较，还需要求线性组合的系数满足规范化条件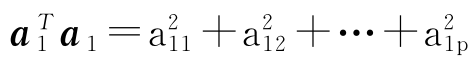＝1。在满足此条件的前提下，力求第一个综合变量f₁的方差var（f₁）达到最大。

若变量f₁包含的信息尚不足以代表原有变量，则需建立第2个综合变量

为了分析和处理的方便，要求各综合变量间互不相关，即应使它们的协方差为零，对f₁和f₂而言，则有cov（f₁，f₂）＝0。在满足互不相关条件与规范化条件＝1的前提下，也要使第二个综合变量f₂的方差var（f₂）达到最大。在变量f₁与f₂所包含的信息尚不足以代表原有变量时，还要构造第三、第四、…，第n个综合变量f₃，f₄，…，f_n。这些综合变量就是本章要讨论的主成分。

设p维向量x的p个变量为x₁，x₂，…，x_p，它们的线性组合构成m（m≤p）个综合变量为

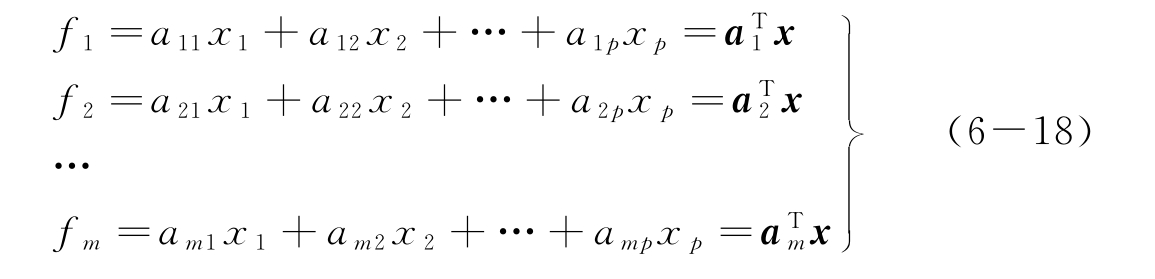
在满足规范化条件

与互不相关条件

的前提下，方差var（f_i）达到最大，则称f_i为向量x的第i个主成分。

按照定义，要确定p维向量x的主成分，相当于在p维空间找出一组正交的单位矢量｛a_i，i＝1，2，…，m｝，并能使方差var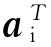x）达到最大。

根据方差与协方差的定义可以证明

由于协方差矩阵Z为正定实对称矩阵，由矩阵代数的性质，它的p个特征值一定大于等于零，设它们为而且一定存在p个相互正交的单位特征矢量与这p个特征值相对应，设它们为u₁，u₂，…，u_p，可以组成一个正交矩阵U＝（u₁，u₂，…，u_p）。于是协方差矩阵Z有分解式

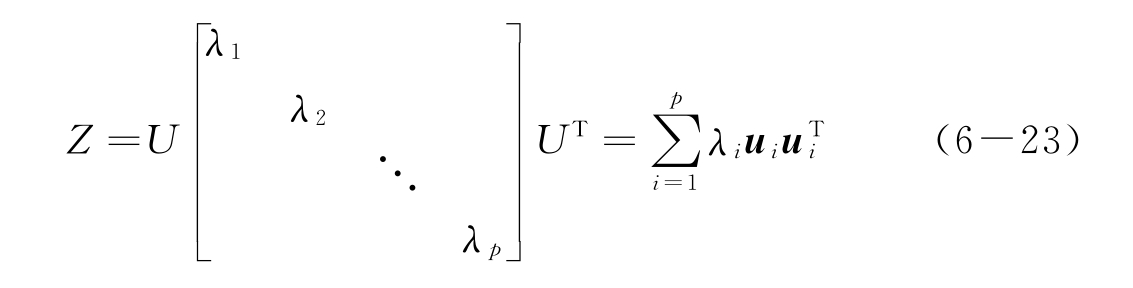
在条件a^Ta＝1下，由方程（6－18）～方程（6－20）可以得到

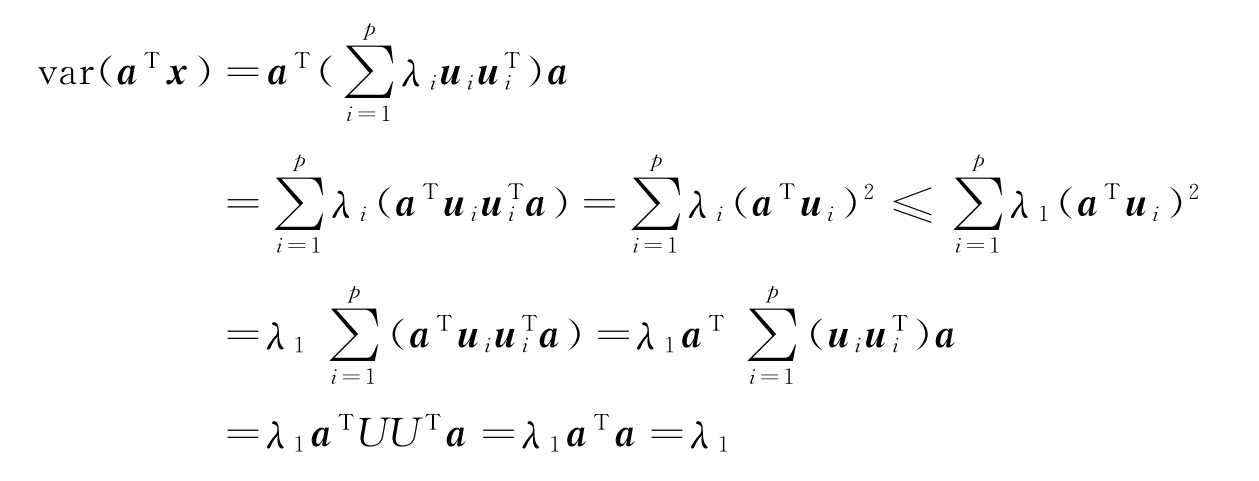
可见在条件（6－20）下，λ₁是var（a^Tx）的上确界，而在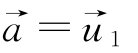时有

因此，可以得出f₁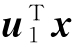＝是向量x的第一主成分。类似地可以证明，在条件a^Tu₂＝0与a^Ta＝1下，var（a^Tx）的上确界为λ₂，而在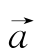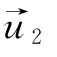＝时有var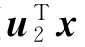）＝λ₂，记f₂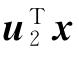＝，则有

因此f₂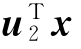＝是向量x的第二主成分。以次类推，f_i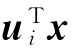＝是向量x第i个主成分，其对应的方差为var（f_i）＝var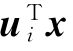（）＝λ_i（i＝3，4，…，p）。对于p维向量x，总共可以导出p个主成分。

实际上，零特征值所对应的主成分，其方差也为零。这样的主成分并没有包含原有变量的信息。另外，方差很小的主成分所包含的信息量也很少，这些主成分都可以略去。因此，通常只保留前m（m＜p）个主成分以替代原有的p个变量。m到底取多大，将在后面讨论。