间接测量结果的误差计算

2.3.3　间接测量结果的误差计算

大多数实验的最后结果都是间接的数值，因此个别测量的误差，都反映在最后的结果里。在间接测量误差的计算中，可以看出直接测量的误差对最后的结果产生多大的影响，并可了解哪一方面的直接测量是误差的主要来源。如果我们事先预定最后结果的误差限度，即各直接测量值可允许的最大误差是多少，则由此可决定如何选择适当精密度的测量工具。仪器的精密程度会影响最后结果，但如果盲目地使用精密仪器，不考虑相对误差，不考虑仪器的相互配合，非但丝毫不能提高结果的准确度，反而枉费精力并造成仪器、药品的浪费。

1.间接测量结果的平均误差和相对平均误差

首先来看一下普遍情况。若要求的数值u是两个变数α和β的函数，即u＝f（α，β）。直接测量α，β时其误差为Δα、Δβ，它所引起数值u的误差为Δu，当误差Δu、Δα、Δβ和u，α，β相比较是很小时，可以把它们看做微分du，dα，dβ。应用微分公式时可写成

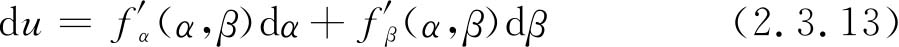
式中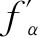，（α，β）为函数f（α，β）对α的偏导数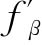；（α，β）为函数f（α，β）对β的偏导数。按照定义其相对误差为

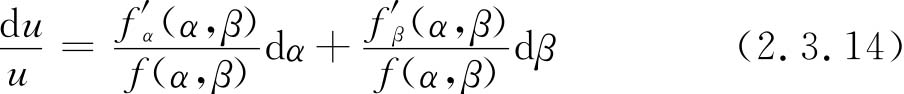
或者是

dlnu＝dlnf（α，β）　　　　　（2.3.15）

故计算测量值u的相对误差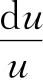可先对u表示式取自然对数，然后直接按照测量的数值对此对数求微分（这里把这些测量数值当做变数）。示例如下：

（1）单项式中的相对误差。设

式中，p、q、r、s是已知数值；k是常数；a，b，c，e是实验直接测定的数值。对上式取对数

lnu＝lnk＋plna＋qlnb－rlnc－slne　　　　　（2.3.17）

对（2.3.17）式取微分

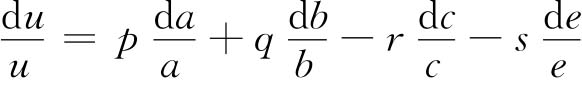
我们并不知道这些误差的符号是正还是负，但考虑到最不利的情况下，直接测量的正、负误差不能对消而引起误差的积累，故取相同符号。最后

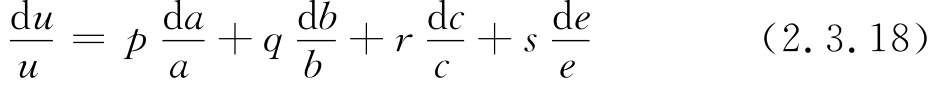
这样所得的相对误差是最大的，称为误差的上限。从（2.3.18）式可见，若n个数值相乘或相除时，最后结果的相对误差比其中任意一个数值的相对误差都大。

（2）对于其他不同运算过程中相对误差的计算列于表2－3中。

表2－3　　　　　　不同运算过程的绝对误差和相对误差

（3）误差举例。

例1　误差的计算

液体的摩尔折射度公式为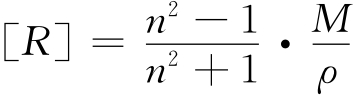，苯的折射率n＝1.4979±0.0003，密度ρ＝0.8737g／cm³±0.0002g／cm³，摩尔质量M＝78.08g／mol。求间接测量［R］的误差是

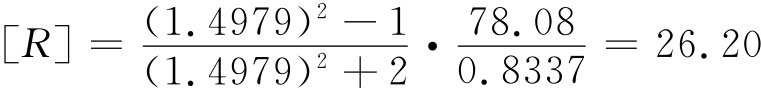
把折射度公式两边取对数并微分，

dln［R］＝dln（n²－1）－dln（n²＋2）－dlnρ

整理得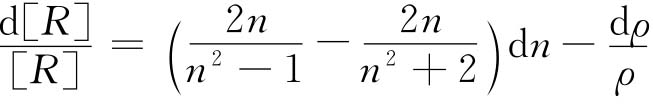　　

代入有关数据d［R］＝0.019

则其相对误差为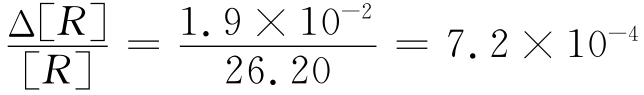

例2　仪器的选择。

用电热补偿法在12mol水中分次加入KNO3（固体）的溶解热测定中，求KNO3在水中的积分溶解热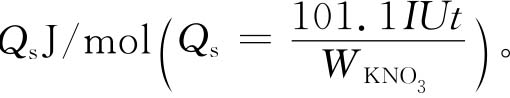如果把相对误差控制在3%以内，应选择什么样规格的仪器？

在直接测量中各物理量的数值分别为：电流I＝0.5A，电压U＝4.5V，最短的时间t＝400s，最少的样品量W_KNO3＝3g。

误差计算：

lnQ_s＝lnI＋lnU＋lnt－lnW

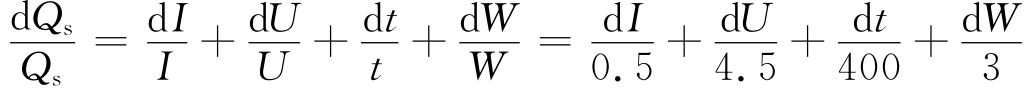
由上式可知最大的误差来于测定I和U所用电流表和电压表。因为在时间的测定中用停表误差不会超过1s，相对误差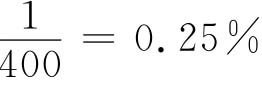。称KNO3如用分析天平只要读至小数后第三位即dW＝0.002g，相对误差仅为0.07%（称水只需用台天平，dW虽为0.2g，但其相对误差为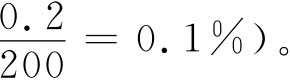。电流表和电压表的选择以及在实验中I、U的控制是本实验的关键。为把Qs的相对误差控制在3%以下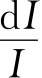，和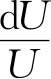都应控制在1%以下。故需选用1.0级的电表（准确度为最大量程值1%），且电流表的全量程为0.5A。电压表的全量程为。

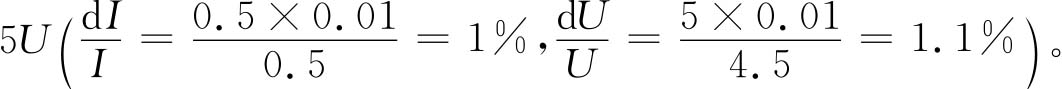例3　测量过程中最有利条件的确定。

在利用惠斯登电桥测量电阻时，电阻R_x可由下式计算：

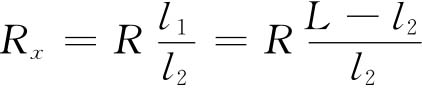
式中，R是已知电阻；L是电阻丝全长（l1＋l2＝L）。因此，间接测量R_x的误差取决于直接测量l2的误差：

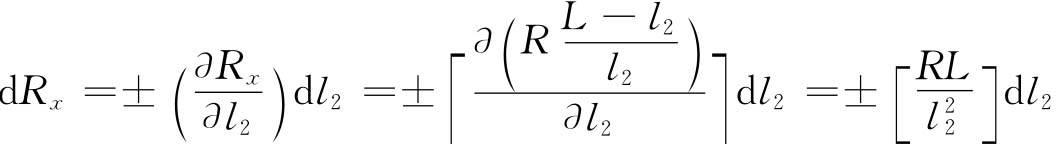
相对误差为

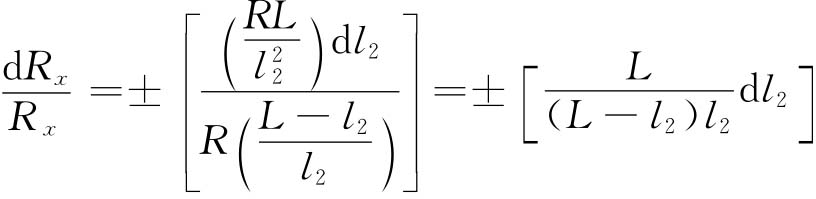
因为L是常量，所以当（L－l2）l2为最大时，其相对误差最小，即

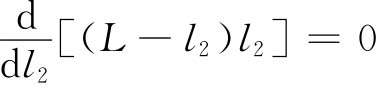
故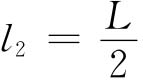　　　　　　　　　　

所以用惠斯登电桥测量电阻时，电桥上的接触点最好放在电桥中心。由测量电阻可以求得电导，而电导的测量是物理化学实验中常用的物理方法之一。

2.间接测量结果的标准误差估计

设函数为u＝f（α，β，…），式中α，β，…的标准误差分别为σα，σ_β，…，则μ的标准误差经推演为

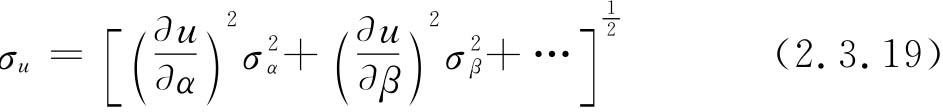
如用测定气体的压力（p）和（V）及理想气体定律确定温度（T）。已知σp＝±13.33Pa，σV＝±0.1cm³，σn＝±0.001mol，p＝6665Pa，V＝1000cm³，n＝0.05mol，R＝8.317×10⁶cm³·Pa·mol^－1·K^－1.

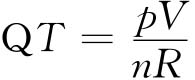
故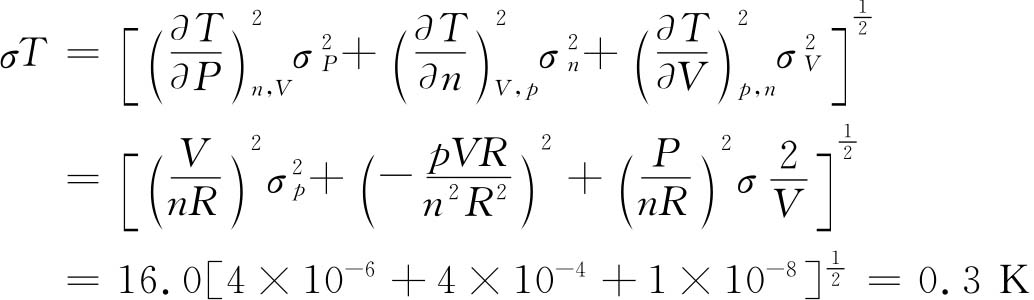　　

最终结果为16.0±0.3K。

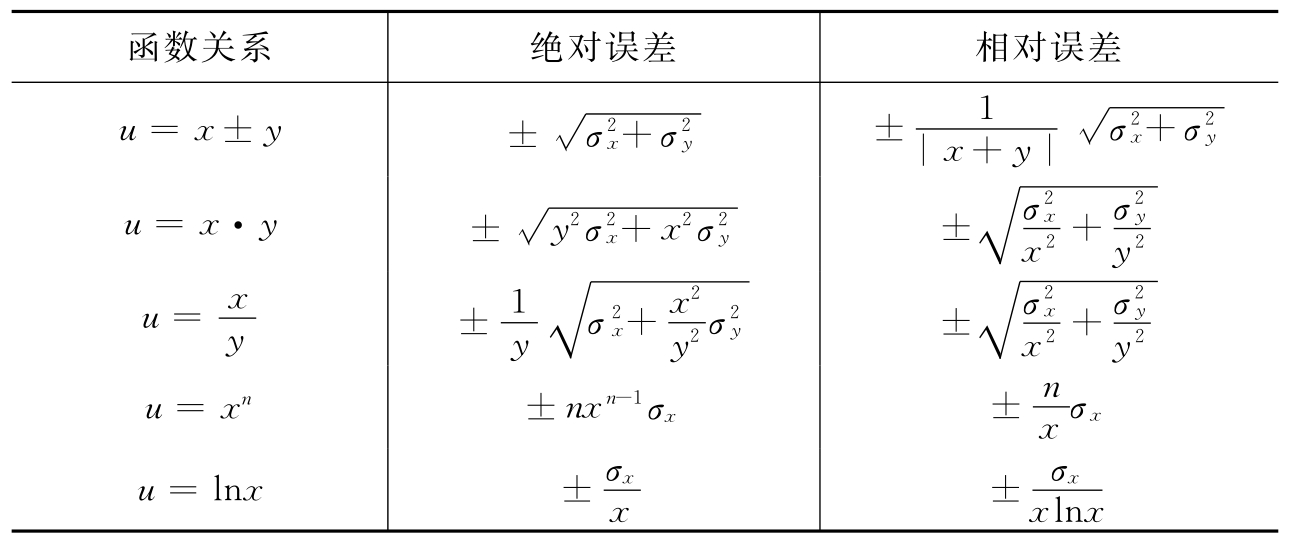
部分函数的标准误差列于表2－4中。

表2－4　　　　　　部分函数的标准误差