在上一章中，我努力指出：原则上，数学证明如何可以完全形式化。如果从特定的公理开始，遵循特定的规则，最后以有趣的数学陈述结束，那么这样的陈述就可以当作定理接受，否则就不能被视为定理。这种思想，即从少数几条公理出发演绎推导出许多复杂的定理，可以追溯到欧几里得。欧几里得只用了五条公理就建立起几何学的主要体系。（关于他的公理，我们将在第六章中讨论。）有人可能提出这样的问题：为什么直到20世纪，人们才认识到这样的思想可以应用于整个数学系统当中呢？
主要的原因可以被归结为一个词：无穷。出于种种原因，无穷这一概念在数学中必不可少，但却很难严格化。在本章中，我将讨论三条陈述。其中每一条乍看起来都普普通通，但经过仔细的考察，会发现最终都涉及到无穷。随之就产生了困难，本章的主要内容就是如何处理这样的困难。
上面这条简单陈述仅仅在说一个不大的数差不多等于另一个数，哪里涉及到无穷了呢？答案就藏在“2的平方根”这个短语里面，这个短语隐含假设了2的确存在一个平方根。要想透彻地理解这条陈述，我们就必须问一问，2的平方根究竟是个什么样的对象。于是无穷就来了：2的平方根是一个无穷小数。
注意，下面这条紧密相关的陈述就不涉及无穷的问题：1.414 213 56的平方约为2。这条陈述完全是有限的，但是看起来所谈论的基本上是同样的事情。我们稍后就能看到，这一点至关重要。
说一个无穷小数的平方等于2，这是什么意思呢？在学校里，我们学过有限小数如何相乘，但从没学过无穷小数的乘法——不知出于什么缘故，我们仅仅假设它们能够参与加法和乘法，而不去深究。这运算应该如何完成呢？为了看看会出现何种困难，我们先来考虑加法。当我们把两个有限小数相加时，比方说2.3859加3.1405，我们将一个数写在另一个数下面，从右向左将对应的数位相加。我们从最末端的数位开始做加法——9加5，得到14，于是写下4，并进1。接下来，我们再加倒数第二位——5加0，以及进上来的1，得到6。依此类推，我们就得到了最终的结果5.5264。
现在假设有两个无穷小数。我们不可能从最右端开始，因为无穷小数根本没有最后一位。那么我们要如何把它们相加呢？有一个明显的回答：从左端开始。然而这么做是有缺陷的。譬如，我们再来加有限小数2.3859和3.1405，先加2和3，得到5。接下来再加3和1，得到4，很不幸，这是不对的。
这个错误给我们造成了一点麻烦，不过只要我们保持勇气继续下去倒也没什么大不了的。接下来要相加的两个数字是8和4，我们可以在这第三位上记下一个2，然后将上一位的4改为5加以修正。这个过程还会出现，在第四位我们会先写下一个5，然后修正为6。
注意，这样的修正有可能会在写下该位结果的很久之后才出现。例如，我们要计算1.355 555 555 555 555 557 3加2.544 444 444 444 444 445 2，会首先写下3.899 999 999 999 999 99，但再往下算一位，即7加5时这一连串的9就不得不修正。就像一连串多米诺骨牌一样，这些9一位接一位地变为0。不过这样的计算方法仍然是行得通的，最后得到计算结果3.900 000 000 000 000 002 5，它让我们能够对如何将无穷小数相加赋予意义。不难看出，没有哪一位数需要修正一次以上，所以如果我们有两个无穷小数，那么两数之和的第53位（打个比方），要么是我们在上述过程的第53步写下的那个数，要么是之后修正的那个数——如果有必要修正的话。
我们想要对这一论断赋予意义：存在一个无穷小数，其平方为2。要做到这一点，我们必须首先看一看这个无穷小数是怎样产生的，然后再去理解让它和自己相乘意味着什么。可以预料到，无穷小数的乘法会比加法更为复杂。
首先，有一个产生这个小数的很自然的办法。这个数肯定在1和2之间，因为12=1，小于2，而22=4，大于2。如果你一一计算1.12，1.22，1.32，一直到1.92，你会发现1.42=1.96小于2，而1.52=2.25大于2。所以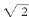
必然在1.4和1.5之间，因此它的小数展开一定是以1.4开头。现在假设你已经以此办法算出
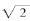的前八位数字是1.414 213 5。你可以继续如下的计算，得到下一位数字是6。
1.414213502=1.9999998236822500
1.414213512=1.9999998519665201
1.414213522=1.9999998802507904
1.414213532=1.9999999085350609
1.414213542=1.9999999368193316
1.414213552=1.9999999651036025
1.414213562=1.9999999933878736
1.414213572=2.0000000216721449
重复这一过程，你想算出多少位都可以。虽然这样的计算永远无法结束，但是你至少有了一种清晰明了的方法，能给定小数点后第n位的数字，无论n取何值：小数点后有n位数，平方不大于2的最大小数，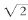
的小数点后第n位数字就与它的最后一位相同。例如，在所有小数点后有两位的小数中，1.41是平方不大于2的最大的一个，所以
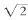展开到小数点后两位是1.41。
让我们记最终得出的无穷小数为x。是什么让我们能够坚信x2=2呢？我们可能会给出如下的理由。
12=1
1.42=1.96
1.412=1.9881
1.4142=1.999396
1.41422=1.99996164
1.414212=1.9999899241
1.4142132=1.999998409469
1.41421352=1.99999982368225
1.414213562=1.9999999933878736
上述算式列表显示了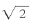
的小数展开位数越多，自身相乘得到的小数点后的数字9就越多。因此，如果把
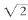完整地展开到无穷多位，我们应该得到无穷多个9，而1.99999999…（9无限循环）等于2。
这样的论述会导致两个困难。其一，为什么1.999999…等于2？其二，也是更严重的一个问题，“完整地展开到无穷多位”是什么意思？这是我们首先想努力搞懂的问题。
为了解决第一个困难，我们必须再次搁置一切直觉。在数学中，人们的确普遍认为1.999999…等于2，但这个事实并不是经由某种形而上学的推理过程发现的。相反，它只是种传统习惯。但这也绝不是毫无理由的传统，因为如果不采纳它，我们就必须发明怪异的新对象，或者抛弃一些熟悉的算术规则。比如，如果你坚持1.999999…不等于2，那么2-1.999999…是什么呢？如果这是0，那么你也就抛弃了一条有用的规则：若x-y=0 ，则x必定与y相等。如果这不是0，那这个数就没有通常的小数展开（否则，你从2中减掉这个数，得到的就不是1.999999…，而是较小的别的数），所以你必须创造一个新的对象，诸如“0加小数点后无穷多个0，之后是个1”。如果做这样的事，那你的麻烦才刚刚开始。这个神秘的数自乘是什么东西呢？小数点后无穷多个0，之后再来无穷多个0，之后是个1？如果你用它乘以10呢？你得到的是不是“无穷多减1”个0，之后是个1？1/3的小数展开是什么呢？用它乘以3，答案是1还是0.999999…？如果你遵循了惯用的传统，这一类难以对付的问题就不会产生了。（虽难以对付，但也并非全然不可能：在1960年代，亚伯拉罕·罗宾逊发现了对“无穷小”数的一个条理清晰的定义，但正如其名“非标准分析”所暗指的，这套理论还没有成为数学界的主流部分。）
第二个困难是更实实在在的困难，但它也是可以绕过去的。我们不去试图想象对无穷小数进行长乘计算，而仅仅将陈述x2=2解释为，x展开位数越多，平方的结果就越接近2，一如我们已经观察到的。为了更确切地说明这一点，假设你仍然坚持想要一个数，它的平方以1.9999…开始。我会向你建议1.414 21这个数，它是由x的前几位给出的。因为1.414 21很接近1.414 22，我预期它们的平方也会很接近（这很容易证明）。但根据我们选择x的办法，必然有1.414 212小于2而1.414 222大于2。因而这两个数都很接近于2。只要检查一下：1.414 212=1.999 989 924 1，于是我们就找到了满足条件的一个数。如果你想要一个新的数，其平方开始几位是
1.999999999999999999999999999999999999999999999999999…
那我可以用同样的办法，只不过多取x几位而已。（事实上，如果你想要n个9，那取到小数点后n+1位就足够了。）无论你想要多少个9，我都可以办到，这一事实正是无穷小数x自乘等于2的含义。
请注意，我所做的是“驯服”无穷，只是将涉及无穷的陈述单纯解读为一种生动的简化，其所指的乃是一条不涉及无穷的累赘得多的陈述。关于无穷的简洁陈述是“x是平方等于2的无穷小数”。可以大致翻译成：“有这样一种规则，对任意n，它能够切实地给出x的前n位数字。这使我们能够算出任意长的有限小数，它们的平方接近于2，只要算得足够长，想要有多接近就能有多接近。”
我是不是在说，x2=2这个外表简单的陈述的真正意思其实非常复杂呢？某种意义上我的确是这个意思——这条陈述确实隐含了复杂性；但从更重要的意义上讲，我并非是指这个意思。固然，在不提及无穷的情况下，要定义无穷小数的加法和乘法是很难的，而且我们还必须检查这个复杂的定义遵从第二章中列出的那些规则，诸如交换律和结合律。但是，一旦给出了这个定义，我们就可以再次无拘无束地进行抽象思考。关于x，重要的是它的平方等于2。关于“平方”一词，重要的是它的含义以某种乘法定义为基础，这种定义遵循着恰当的规则。x的第一万亿位是什么并不是真正紧要的，乘法的定义有多复杂也不真正紧要。
假设你坐在一辆正在加速的小轿车里，看着速度表的指针稳定地从时速30英里移动到时速50英里。我们很容易说，在某个时刻——恰在指针扫过40的那一瞬间——汽车以时速40英里的速度行驶。在那个时刻以前，车速小于它，在之后车速大于它。但是，说仅在某个瞬间车速为每小时40英里，这是指什么意思呢？如果汽车没有加速，那我们可以测量它一小时走过多少英里，从而得到它的速度。（更具操作性的是，观察它在30秒内走过多远，再乘以120。）但是，这种办法对加速的汽车显然无效：测量它在一段时间内走过多远，只能算出这段时间内的平均速度，并不能得到特定瞬时的速度。
如果我们能够测量在无穷小的一段时间内汽车走了多远，那问题就不存在了，因为这样速度就没有时间发生变化。如果这段时间是t小时，t是个无穷小的数，那么我们可以测量汽车在t小时走过多少英里，记测量结果为s，它当然也是一个无穷小的数，用它除以t就得到了汽车的瞬间速度。
这种荒唐的幻想引起的问题相当类似于前面遇到的情况，当时我们简要地考察了1.999999…可能不等于2的思想。t是0吗？如果是，那很明显，s必然也是0（没有时间流逝，汽车不能走过任何路程）。但是，无法通过0除以0来得到清楚明白的答案。如果t不是0，那在这t小时之内汽车就会加速，从而导致测量无效。
要想理解瞬时速度，我们就要利用这样的事实：如果t非常小——比如百分之一秒，则汽车没有时间去加速太多。设想对于某个时刻，我们不去试图计算确切的速度，改而用一个较准的估计来代替。这样，如果我们的测量装置是精确的，我们就能知道汽车在百分之一秒内走了多远，然后把这段距离乘上一小时内百分之一秒的数量，即乘以360 000。这个答案并不会特别准确，但既然汽车在百分之一秒内加速不多，这个答案就给了我们一个相当接近的近似值。
这个情况让我们回想起1.414 213 52相当近似于2这一事实，于是类似地，我们可以不用再操心无穷，或者说是本例中的无穷小。假设我们不是在百分之一秒内测量，而改为在百万分之一秒内测量，那汽车的加速就更少了，因而得到的答案会更加精确。这种观察让我们有了一种办法，可以把陈述“汽车此刻的行驶速度是40英里每小时”转换成以下这条更复杂的、不涉及无穷的陈述：“如果你给定了允许的误差范围，那么只要t足够小（远小于1），我就可以测出汽车在t小时内走过的英里数，再除以t，得到的结果将很接近于40英里每小时，误差在你规定的范围之内。”例如，如果t足够小，我可以保证使我的估计值位于39.99和40.01之间。如果你要求我的答案精确到误差小于0.0001，那么我可以使t变得更小。只要它足够小，我总可以满足你要求的精度。
我们再一次把一条涉及无穷的陈述，视为对一条更复杂的、关于近似的命题的方便表达。另一个更具提示性的词语是“极限”。一个无穷小数是一列有限小数的极限，瞬时速度是通过测量越来越短的时间内走过的距离所得近似值的极限。数学家经常谈论“在极限时”或者“在无穷时”的情况如何，但他们都很明白，他们并没有把这种说法完全当真。如果强迫他们说出确切意思，他们就会转而谈论近似。
无穷可以借由有穷的情况来理解——人类对这一点的认识就是19世纪数学的伟大胜利之一，不过这种思想的根源能够追溯到更早。我的下一个例子是讨论圆面积的计算，就将使用阿基米德在公元前3世纪所提出的论证。不过，在开始计算以前，我们应当明确要算的是什么，这个问题并没有乍看上去那么简单。什么是面积？当然，它是图形里某种东西的量（二维的东西），但怎样才能精确表达呢？
不论它是什么，对特定形状来说，它看起来当然是很容易计算的。例如，如果矩形的边长为a和b，那它的面积就是ab。任何直角三角形都可以被看作把矩形沿一条对角线切下一半所得，因此它的面积是对应矩形面积的一半。任意三角形都可以分割成两个直角三角形，任意多边形都可以分割成一系列三角形。因此，要算出多边形的面积并不会太难。不必去烦恼我们算的到底是什么，我们只要单纯地将多边形的面积定义为此计算结果即可（只要我们能够确信，将多边形切割成三角形的不同方法不会导致不同的答案）。
当我们考虑边缘为曲线的图形时，问题就来了。将圆切割成若干个三角形是不可能的。那么当我们说圆的面积是πr2时，我们谈的是什么呢？
这又是抽象方法大有用处的一个例子。让我们不要关注面积是什么，而是关注面积能够做什么。我们要对这个说法作一些澄清，因为面积看上去做不了什么事情——它只不过是就在那里而已。我所说的意思是，我们应当关注，关于面积的任何合理概念所应具有的一些属性。下面列出了五条。
Ar1 移动图形，图形面积不变。（更正式的说法：两个全等的图形面积相等。）
Ar2 如果一个图形完全包含于另一个之内，那么第一个的面积不大于第二个。
Ar3 矩形的面积通过它的长宽相乘得到。
Ar4 将图形切成若干部分，则各部分面积之和等于原图形的面积。
Ar5 图形向各方向扩张为原来的2倍，则图形面积变为原来的4倍。
如果回过头来看，你会发现我们利用了属性Ar1、Ar3和Ar4来计算直角三角形的面积。属性Ar2看起来非常显然，几乎无须一提，不过作为公理正应如此，而且我们后面还会看到它会多有用。属性Ar5尽管很重要，其实并不需要作为一条公理，因为它能从另外几条中推导出来。
我们怎样利用这些属性来谈论圆面积的含义呢？截至目前，这一章所要向读者传达的信息就是，不要考虑一步到位的定义，考虑面积的近似可能会有收获。我们可以采取下面这种办法轻易做到。想象一个图形画在一张布满细密方格的纸上。由属性Ar3，我们知道这些方格的面积（因为正方形只是特殊的矩形），所以我们可以数一数有多少正方形完全处于图形以内，以此来估计图形的面积。举例来说，图形中包含了144个小方格，那么图形的面积至少是144乘以单个方格面积。注意，我们所真正计算的面积仅是144个方格所构成的图形的面积，此面积由属性Ar3和Ar4可以很容易地确定。
对于图18所示的图形，这并不能给出正确的答案，因为还有若干个方格部分位于图形之内、部分位于图形之外，我们还没有计入它们的面积。不过，有一种改进估值的明显方法，就是把每一个小方格分成四个更小的方格，改用它们来计算。和之前一样，又有一些方格部分位于图形外、部分位于图形内，但这回我们已经多包含进了一些完全在图形之内的小方格。一般来说，方格划分得越密，我们在计算中能够计入的原图面积也就越多。我们发现（这一点并没有看上去那么显然），随着把网格画得越来越密，方格越来越小，计算的结果也就越来越接近于某个数，就像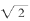
近似值的平方越来越接近于2一样，于是我们就将这个数定义为这个图形的面积。
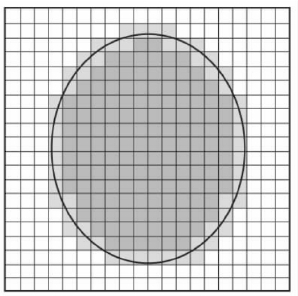
图18 曲线图形面积的逼近
所以，从数学的角度来讲，某个图形的面积为一平方码的含义是这样的：在特定的容许误差范围之内，无论多小，总可以找出充分密集的方格，由位于图形内的小方格来近似计算，得到的计算结果与一平方码之差少于给定误差。（在脑子里某处可能有这样的想法——但已经被压制住了：“在极限下”可以使用无穷多无限小的方格来得到确切的答案。）
还有另外一种说明方法，也许能够说得更清楚。如果一个曲线图形的确切面积是12平方厘米，要求我用方格法来表明这一点，这个任务是不可能完成的——我需要用无穷多的方格才能做到。但是，如果你给出任何其他不同于12的数字，比方说11.9，那我都可以用一套方格来确定地证明它的面积不是这个数：我只需使网格足够密，让没有计入的部分小于0.1平方厘米即可。换句话说，在不涉及无穷的情况下，我不去证明它的面积是12，而是满足于证明它的面积不是别的任何数。图形的面积是我所不能证伪的那个数。
这些思想给了面积一个令人满意的定义，但仍给我们遗留下一个问题。我们要怎样来说明，如果采用上述过程来估计半径为r的圆的面积，估计值就会越来越接近πr2呢？对于大多数图形来说，答案是必须使用到积分，我这本书中不会去讨论它。但对于圆来说，正如我之前所提到的，我们可以使用阿基米德的绝妙论证。
图19表示的是，将圆切成一片一片，再组合成接近于矩形的形状。因为每一小片都很窄，所以矩形的高度大约为圆的半径r。同样因为每一片很窄，这个准矩形的上边和下边都近似于直线。上下两边各用了圆的周长的一半，由π的定义知圆的周长为2πr，则两边长度均近似为πr。因此，准矩形的面积是r×πr=πr2——至少是近似如此。
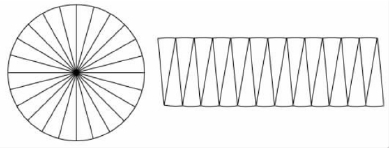
图19 阿基米德说明圆面积为πr2的方法
当然了，事实上准矩形的确切面积就是πr2，因为我们所做的只不过是把圆切开，再移动各部分而已，但是我们目前还不知道这一点。到现在为止，这个论证可能已经使你确信了，但其实还没结束，因为我们还必须表明，随着切开的片数越来越多，上述近似值会越来越接近πr2。一种非常简明的方法是利用两个正多边形，一个恰好包含在圆内，一个恰好包含圆。图20用六边形说明了这一点。内接多边形的周长小于圆的周长，而外切多边形的周长大于圆的周长。这两个多边形都可以切成多个三角形，再拼合成平行四边形。一点简易的计算就能够表明，较小的平行四边形面积小于r乘以内接多边形周长的一半，因而小于πr2。类似地，较大的多边形面积大于πr2。如果切出的三角形数量足够大，那么这两个多边形面积之差就会越来越小，想要多小就有多小。因为圆总是包含着小多边形，并被大多边形所包含，所以它的面积必然恰为πr2。
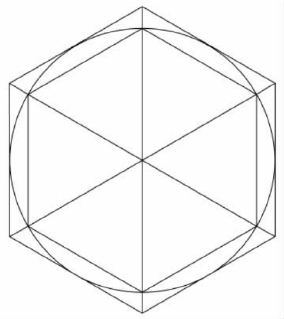
图20 由多边形逼近圆
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
