罗尔定理构造辅助函数

极值与Fermat（费尔马）定理

微分中值定理的建立源于函数极值的研究。为此，我们首先介绍极值概念与性质。

定义4.1.1　设函数f在x₀的某个邻域内有定义。如果存在δ＞0，使得对任何x∈（x₀－δ，x₀＋δ），恒有

f（x）≤f（x₀），

则称f（x₀）为函数f的一个极大值，x₀为f的一个极大值点。类似地可以定义f的极小值和极小值点。极大值或极小值统称为极值，而极大值点或极小值点统称为极值点。

显然，“极大”或“极小”仅是一个局部概念，不具有整体性。对给定的函数，极大（小）值点可能不存在，也可能存在多个。同样，同一函数的两个极大值有可能不相等。从定义来看，极值点x₀必须是f定义域的内点（需要在x₀的两侧比较函数的大小）。如果f仅在x₀的一侧有定义，则x₀不可能为f的一个极值点。

可微函数的极值点有一个非常容易检验的特点。为说明这一特点，我们假定x₀为f的一个极小值点，则当x₀充分接近x₀时，总有f（x）－f（x₀）≥0．于是，由极限的保号性，

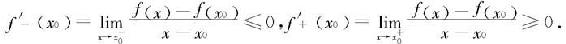
注意到f′－（x₀）＝f′＋（x₀）＝f′（x₀），因此必有f′（x₀）＝0．由此我们证明了下述Fermat定理。

定理4.1.2（Fermat定理）　设x₀为函数f的极值点。如果f在x₀处可微，则

f′（x₀）＝0．

Rolle（罗尔）定理

显而易见，如果可微函数f的最大（小）值f（x₀）在定义区间的内部取到，则这个最大（小）值必定为f的极值，因此，由Fermat定理，f′（x₀）＝0．

有许多不同的条件可以确保f有一个最大或最小值在定义区间的内部取到。Rolle给出了一个简单且容易检验的条件：f在［a,b］上的连续，且f（a）＝f（b）．我们可以分两种情形证明之：

（1）如果f在［a,b］上为常数，则（a,b）内的任何x₀都为f的最大（小）值点。

（2）如果f在［a,b］上不为常数，则存在x₀∈（a,b），使得f（x₀）≠f（a）．不妨设f（x₀）＜f（a）．于是f（a）和f（b）都不是f在［a,b］上的最小值，其最小值必定在区间（a,b）的内部取到。因此我们有下述Rolle定理：

定理4.1.3（Rolle定理）　如果f在区间［a,b］上连续，在（a,b）内可导，且f（a）＝f（b），则存在ξ∈（a,b），使得

f′（ξ）＝0．

从上述证明中我们看到，Rolle定理中的介值点ξ可以是一个最大或最小值点。

例4.1.4　设α∈（0,π），f（x）＝（x－α）sinx，则存在ξ∈（0,π），使得f″（ξ）＝0．

证明　显然f二阶可导。因为f（0）＝f（α）＝f（π）＝0，所以根据Rolle定理，在（0,α）和（α,π）内分别存在ξ₁和ξ₂，使得f′（ξ₁）＝f′（ξ₂）＝0．易知，f′在［ξ₁，ξ₂］满足Rolle定理的条件，故对f′再次应用Rolle定理，可知存在ξ∈（ξ₁，ξ₂）⊂（0,π），使得f″（ξ）＝0．　　□

该例题可以用其他方法证明，但用Rolle定理显得简单、方便。

Lagrange（拉格朗日）定理

Rolle定理的条件“f（a）＝f（b）”意味着连接两点（a，f（a））和（b，f（b））的直线是一条水平线，而结论“f′（ξ）＝0”表明f在点（ξ，f（ξ））处的切线也是一条水平直线。Rolle定理的本质是：连接两点（a，f（a））和（b，f（b））的直线与曲线上某点的切线是平行的，尽管这里的“平行”还有一点点特殊性：水平平行。这一平行的本质特性在条件“f（a）＝f（b）”不能满足时也能保持。下述Lagrange定理说明了这一点。

定理4.1.5（Lagrange定理）　如果f在［a,b］上连续，在（a,b）内可导，则存在ξ∈（a,b），使得

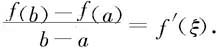
该定理可以通过构造一个满足Rolle定理条件的函数g来获证。令

g（x）＝f（x）－l（x），

其中是过两点（a，f（a））、（b，f（b））的直线函数。容易验证g（x）满足Rolle定理的三个条件，故g′有一个零点ξ∈（a,b），等价地，

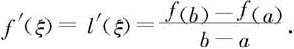
从而证明了Lagrange定理。

注　拉格朗日中值定理又称微分中值定理。

推论4.1.6　若f′在（a,b）内存在且恒为零，则f在（a,b）内为常数。

证明　这个推论非常明显：对（a,b）内的任何两点x₁＜x₂，根据Lagrange定理，存在ξ∈（x₁，x₂），使得

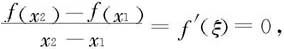
从而

例4.1.7　证明：在［－1,1］上有恒等式：

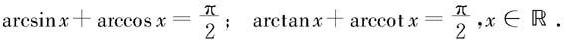
解　直接计算导数，得（arcsinx＋arccosx）′＝0．因此由推论4.1.6，

其中C为常数。再令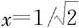即可确定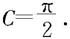类似地可导出第二个恒等式。

由Rolle定理或Lagrange定理可以推导出一些检验函数单调性的判别方法。我们将在下节详细讨论。

Cauchy（柯西）定理

不难看出，Lagrange定理是Rolle定理的推广。更为一般的结论是下述Cauchy定理。

定理4.1.8（Cauchy定理）　设函数f和g在［a,b］上连续，在（a,b）内可导，且g′在（a,b）内没有零点，则存在ξ∈（a,b），使得

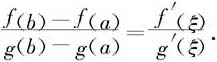
关于Cauchy定理，我们有这样一些说明：根据Rolle定理的推论，在g′≠0的条件下，必然有g（a）≠g（b）．因而上述等式两边分式的分母非零。然而条件“g′≠0”不是本质的。只要将上式改写为

（f（b）－f（a））g′（ξ）＝（g（b）－g（a））f′（ξ），

那么在去掉“g′≠0”的条件下，上式仍然成立。

有许多方法可以证明Cauchy定理。比较常见的是采用构造一个满足Rolle定理条件的辅助函数，如同证明Lagrange定理的情形。不过我们这里提请读者考虑这样一个问题：是否可以由Lagrange定理直接导出Cauchy定理？

为此，令α＝g（a），β＝g（b）．由于条件“g′＝0”隐含着g严格单调（参见定理4.2.3），故其反函数g^-1存在。于是a＝g^-1（α），b＝g^-1（β），并且

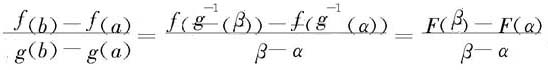
其中复合函数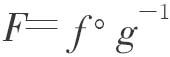在定义区间［α,β］上连续（假定α＜β），在其内部可微。另一方面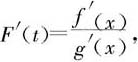，其中x＝g^-1（t）．因此，对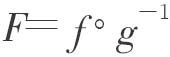在区间［α,β］上应用Lagrange定理，立即得到所需的结论。

上述中值定理的介值点ξ可以表示更为方便的形式：

ξ＝a＋θ（b－a），

其中θ∈（0,1）．

例4.1.9　设b＞a＞0，f在［a,b］上连续，在（a,b）内可导。则存在ξ∈（a,b），使得

证明　若将与ξ无关的因子移到等式另一边，则所要证明的是：存在ξ∈（a,b），使得

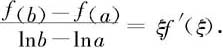
接下来的证明就非常显然了：令g（x）＝lnx，并应用Cauchy中值定理。请读者完成之。