弯曲半径和曲率的区别

6-3　我们的空间是弯曲的

下面讨论主要的问题。上一节所说的有没有道理呢？更确切地说，我们生活于其中的现实的三维空间是弯曲的吗？人类一旦有了足够的想像力去认识这样一种可能性，即空间有可能是弯曲的，头脑中自然就会产生好奇心，渴望知道真实世界是否是弯曲的。为了尝试找到答案，人们做过直接的几何测量，但并未发现对平直的任何偏离。另一方面，通过对引力问题的讨论，爱因斯坦发现，空间确实是弯曲的，不过，我倒是愿意向各位讲一讲有关曲率数值的爱因斯坦定律讲的是什么，还要讲一讲有关他如何发现这个定律的一些故事。

爱因斯坦认为，空间是弯曲的，物质是弯曲的起因（物质也是引力的起因，因此引力与弯曲相对应——不过，这一点将在本章稍后再做介绍）。为了使事情更容易一点，我们设想，物质以某种密度连续分布，不过，物质的密度是可以随你所愿而到处不一样的，12爱因斯坦给出的有关曲率的规则如下：如果存在一个有物质分布于其中的空间区域，我们取一个足够小的球面，使其中的物质密度ρ近似为常数，那么，这个球面的半径超出量正比于球面内的质量。利用半径超出量的定义得到

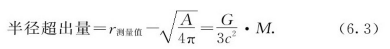
式中G是（牛顿理论中的）万有引力常数，c是光速，M=4πρr3/3是球面内的物质的质量。这就是空间平均曲率的爱因斯坦定律。

假定取地球做例子，并忽略密度处处不一样这个实际情形——这样就不需要做积分了。假定我们打算非常仔细地测量地球的表面，然后挖一个通向地心的洞并测量它的半径。利用表面积可以计算出预期的半径，这个半径可以通过令面积等于4πr2而得到。如果把预期半径与实测半径做比较，就会发现，实测半径比预期半径大，超出的数值由公式（6.3）给出。常数G/3c2大约等于2.5×10-29厘米/克，因此，对于每克物质来说，实测半径偏离预期值2.5×10-29厘米。把地球的质量（大约等于6×1027克）代入公式，结果是，地球的实测半径比根据其表面积预期应该具有的半径值大1.5毫米。13对太阳做同样的计算就会得到，太阳的半径大500米。

大家可能注意到，这条定律说，地球表面上方的平均曲率等于零。但是，这并不表示曲率的全部分量是零。地球上方仍然有可能存在（实际上就是存在）某种曲率。就平面上的一个圆来说，在某个指向上，它具有正或负的半径超出量，而在另一个指向上，它却具有正负号相反的半径超出量。这条定律只不过给出这样一个结果，如果球面内部没有质量，那么，对球面做平均就等于零。顺便提一下，这条定律给出，在各个曲率分量与平均曲率随位置的变化之间存在某种关系。因此，假如知道了每一点的平均曲率，就能够计算出每一点上曲率的细节。地球上方的平均曲率随高度而改变，因此，空间是弯曲的。正是这种弯曲，我们把它视为引力。

设想在一个平面上有一只虫子，并假设这个“平面”上几乎没有什么疙瘩。无论在哪里有一个疙瘩，这只虫子就会断定，它的空间有少许弯曲的局部区域。在三维中，我们有相同的推断。无论在哪里有物质团块，我们的三维空间就有局部的弯曲——一种三维的疙瘩。

假如我们在一个平面上弄上许多肿块，那么，除了所有的疙瘩之外，还有可能存在一种整体的弯曲——表面可能会变得像一个球面。由于存在像地球和太阳这样的物质团块，我们的空间是否就不但具有局部的疙瘩，而且还具有某种净余的平均弯曲，探究一下这个问题是很有意思的。天体物理学家一直在尝试通过测量极其遥远的星系来回答这个问题。例如，我们在一个遥远的球形壳层内看到的星系的数目，不同于从有关这个壳层的半径方面的知识出发预期到的数目，那么，就会得到一个非常巨大的球的半径超出量的实测值。利用这种测量可望探明，我们的整个宇宙到底是弯曲的，还是平均来说平直的——到底是像一个球那样“封闭的”，还是像一个平面那样“开放的”。大家也许听说过有关这个课题的仍然在继续着的争论。存在争论是因为天文测量的结果仍然是完全不确定的；实验数据并没有精确到足以给出一个明确的答案。遗憾的是，有关我们的宇宙在大尺度上整体弯曲的状况，我们一点都不知道。