圆均匀光波导

1.圆均匀光波导的基本概念

横截面为圆面的光波导称为圆光波导。工程技术中使用的光纤大都是圆光波导。如果一个圆光波导是均匀光波导，且其横截面可分为一系列同心环域，每个环域内折射率均匀，则称其为圆均匀光波导或同轴光波导。圆均匀光波导是最简单且使用最广泛的光波导。图4.3.1（a）所示为一种最早出现的两层圆均匀光纤，它只有一个芯层和一个包层，芯层直径2a＝50μm，芯层和包层的相对折射率差Δ＝＝1%。这种光纤能传输多个模式，称为多模阶跃光纤。由于多模阶跃光纤的不同模式之间存在严重的由于传输常数不同引起的色散（称为模间色散），限制了通信速率的提高，又出现了梯度光纤，如图4.3.1（b）所示。在梯度光纤的包层内，折射率均匀，而在芯层内按平方律下降，以便降低模间色散，提高通信速率。G.651光纤就是一种梯度光纤。此后，为彻底消除模间色散，人们把芯层半径a减小到了5～10μm，相对折射率差Δ减小到0.5%左右，这样，就制成了单模光纤，如图4.3.1（c）所示。工作于1.3μm波长的单模光纤的模间色散小于3ps／nm·km，几乎等于零，损耗也很小，得到了广泛应用。G.652光纤就是这样一种低色散低损耗光纤，但其最低损耗点不在1.3μm波长而在1.55μm处。为使色散最低点和损耗最低点一致，人们制成了如图4.3.1（d）所示的三层或四层圆均匀光波导，称为色散位移光纤。G.653光纤就是这样一种色散位移光纤。为了对光纤的色散进行补偿，又研制出了多层结构的圆均匀光波导，其色散为负值，称为色散补偿光纤。近几年出现的G.655光纤也是一种圆均匀光波导，具有低损耗、低色散和低非线性的良好性能。总之，圆均匀光波导的研究具有重要的实际意义。

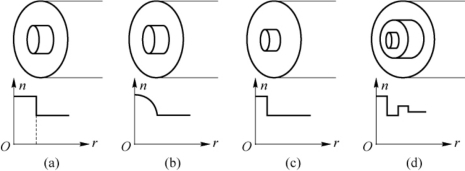
图4.3.1　几种常见的圆均匀光波导

作为均匀光波导，圆均匀光波导中的电磁场为式（4.1.1）：

其中的模式场（振幅）也可以分解为横向和纵向分量的和：

若在极坐标中分解横向分量：

则因分量的方向不固定，称为矢量模。若在直角坐标中分解横向分量：

则因分量的方向固定，称为标量模或线偏振模（LP模）。

2.矢量模

下面来讨论矢量模。将式（4.3.2）代入式（4.1.2），得

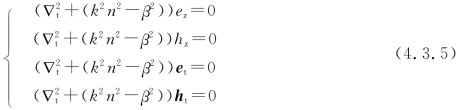
方程组（4.3.5）中的前两个标量方程可以利用分离变量法直接求解，后两个矢量方程中的横向分量由于其分量的方向不固定不能再分解为标量方程。因此，方程组（4.3.5）的求解方法是，先求出纵向分量ez，hz，再利用横向分量和纵向分量的关系式（4.2.7）求出横向分量。这种方法称为矢量法。具体步骤就是，首先在柱坐标中分离变量，得到贝塞尔方程：

和

其中，ri是圆均匀光波导中第i层的半径。解这两个方程，就得到纵向分量ez，hz。

令et＝er＋eφ，ht＝hr＋hφ，并利用极坐标中的表示式：

由式（4.2.7）得

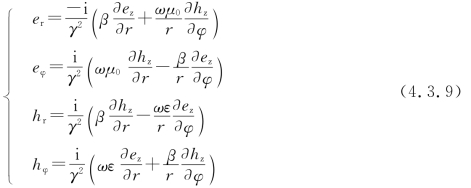
其中，r，φ，z的方向服从右手关系，如图4.3.2所示。上式表明，只要求得两个纵向分量ez，hz，其他分量都可以由上式得到。

下面说明矢量模中可能存在的模式的性质。

如前所说，光波导中不存在TEM模。如果存在TE模，由于ez＝0，由式（4.1.3）第二式得

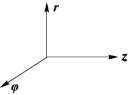
图4.3.2　r，φ，z的方向服从右手关系示意图

这表明横向磁场无旋。同时，由于ez＝0，式（4.3.9）后两式化为

4.4节我们将看到，由于圆对称性，圆均匀光波导中的模式场各分量都具有R（r）sin mφ或R（r）cos mφ的形式，因此，将式（4.3.11）代入式（4.3.10），得

即m＝0。这就是说，对于无旋的横向磁场，m＝0。反之，如果m＝0，由式（4.3.12）可知，必有∇t×ht＝0，即横向磁场无旋，则由式（4.1.3）第二式得ez＝0，此为TE模。同理，对于TM模，由于hz＝0，由式（4.1.3）第一式得∇t×et＝0，这表明横向电场无旋，也有m＝0。反之，如果m＝0，则横向电场无旋，即∇t×et＝0，则由式（4.1.3）第一式得hz＝0，此为TM模。总之，m＝0对应着矢量模中的TE模或TM模，它们的横向磁场或横向电场无旋。

对于TE模，由于ez＝0和m＝0，er＝0，hφ＝0，式（4.3.9）化简为

即et＝eφ，ht＝hφ，二者相互垂直。由上式可知，eφ／hr＝ωμ0／β。如前所说，ωμ0／β为波阻抗。

对于TM模，由于hz＝0和m＝0，eφ＝0，hr＝0，式（4.3.9）化简为

即et＝er，ht＝hφ，二者相互垂直。由上式可知为波阻抗。

总之，TE模和TM模都是偏振方向相互垂直的线偏振波。

如前所说，式（4.3.14）中的ez是m＝0时的贝塞尔方程（4.3.6）的解，而式（4.3.13）中的hz是m＝0时的贝塞尔方程（4.3.7）的解。由此不难理解，对于混合模HE模或EH模，由于ez≠0，hz≠0，其方程组如式（4.3.9）所示，而ez和hz满足m≠0的贝塞尔方程（4.3.6）和方程（4.3.7）。总之，不论TE模、TM模还是混合模，问题都归于求解贝塞尔方程（4.3.6）和方程（4.3.7）。从数学意义上说，式（4.3.6）和式（4.3.7）的解是4类贝塞尔函数的两种线性组合：

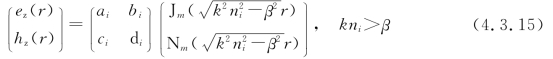
和

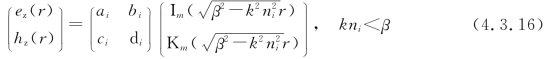
其中，Jm，Nm，Im，Km分别是第一、第二类（Neumann）贝塞尔函数和第一、第二类变型贝塞尔函数，这四类贝塞尔函数的函数曲线如图4.3.3所示。注意，图4.3.3（a）中的第一类贝塞尔函数Jm是振荡衰减函数，图4.3.3（d）中的第二类变型贝塞尔函数Km是指数衰减函数（见郭敦仁编《数学物理方法》，人民教育出版社，1965年第1版，第十七章）。

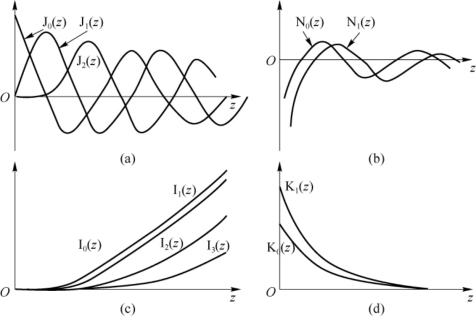
图4.3.3　4类贝塞尔函数的函数曲线图

3.标量模

下面讨论标量模。将式（4.3.4）和∇t＝代入式（4.1.3），得

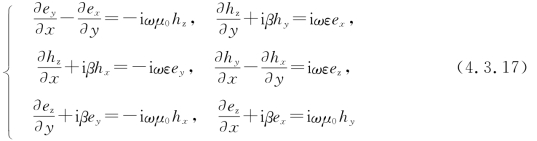
现在来证明，若ex＝0，ey是已知的，模式（0，ey，ez，hx，hy，hz）是式（4.3.17）的解。

由于ex＝0，由式（4.3.17）的前4个式子化为

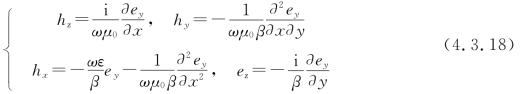
若将上面最后两式代入式（4.3.17）的第五个式子，得

其中，ω2μ0ε＝k2n2。式（4.3.19）是关于ey的波动方程，总是成立的。若将式（4.3.18）的第二和第四式代入式（4.3.17）中最后一个式子，则得到一个关于ey的恒等式。所以，只要从式（4.3.19）解得ey，模式（0，ey，ez，hx，hy，hz）作为式（4.3.17）的解就可确定。该模式称为y方向的偏振模。

同理可证，若ey＝0，ex是已知的，模式（ex，0，ez，hx，hy，hz）也是式（4.3.17）的解，称为x方向的偏振模。而圆均匀光波导中实际的标量模是这两种线偏振模的叠加：

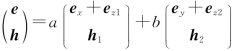
若设式（4.3.18）中的二阶导数项足够小而忽略之，得

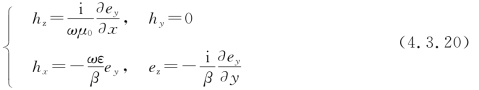
这就是说，波导中电磁波的et＝ey，ht＝hx，二者相互垂直且服从右手法则。注意到ez，hx，hz应在介质分界面上连续，故由式（4.3.20）可知，原本在介质分界面上不连续的ey及其导数连续了。同时，ε沿波导横截面的变化被忽略了，即两介质层的折射率差别很小，这称为弱导条件。所以，关于上述简化，下面的3种说法等价：

（1）模式场的二阶导数是无穷小量。

（2）et＝ey，ht＝hx，二者相互垂直且服从右手法则。这实际上是把电磁场看成了标量场，故上述简化称为标量近似。

（3）ey及其导数连续，两介质层的折射率差别很小。故标量近似也称弱导近似。

总而言之，线偏振模的特征是：

（1）横向分量相互垂直，即x方向偏振模的ex与hy相互垂直，y方向偏振模的ey与hx相互垂直。

（2）电磁场的两个横向分量成比例，比例系数就是波阻抗。如此看来，线偏振模类似于矢量模中的TE模和TM模，但纵向分量ez和hz不等于零。