总自由度
DF T=n-1 (4.2)
产生总变异的原因可从两方面来分析:
①同一处理不同重复观测值的差异是由偶然因素影响造成的,即试验误差,又称组内变异。
②不同处理之间平均数的差异主要是由处理的不同效应所造成,称为处理间变异,又称组间变异。
因此,总变异可分解为组内变异和组间变异两部分。
记
式中,SS e为组内的变异,即误差变异,是各个组观测值xij和对应组平均数x·j的变异之和。
组内自由度
![]()
DF e=n-s (4.4)
记
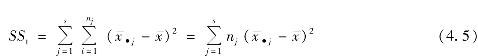
式中,SS t为组间差异,是S个处理的平均数x •j与总平均数x 的变异之和。
组间自由度
DF t=s-1 (4.6)
于是得上表类型资料平方和与自由度的分解式为
总平方和=组间(处理间)平方和+组内(误差)平方和
![]()
即
SS T=SS t+SS e
(4.8)
总自由度=组间(处理间)自由度+组内(误差)自由度
n-1=(s-1)+(n-s) (4.9)
即
DF T=DF t+DF e
(4.10)
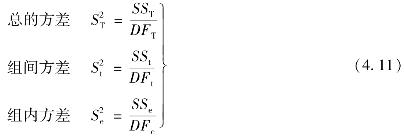
求得各变异来源的平方和与自由度后,进而求得
3)F测验问题
统计学上把组间和组内这两个方差之比值称为F值,即
![]()
上面的分析结果可排成表4.4的形式,称为方差分析表。
表4.4 方差分析表
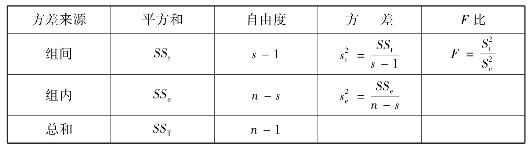
实际进行F测验时,是将由试验资料所算得的F值与根据ν1=DF t(大均方,即分子均方的自由度)、ν2=DF e(小均方,即分母均方的自由度)查附表F值表所得的临界F值与F0.05,F0.01相比较作出统计推断的。
若F<F0.05,统计学上把这一测验结果表述为:各处理间差异不显著。
若F0.05≤F≤F0.01,统计学上,把这一测验结果表述为:各处理间差异显著。
若F>F0.01,统计学上,把这一测验结果表述为:各处理间差异极显著。
在实际中,可按以下较简便的公式来计算SS T,SS t和SS e:
记

即有
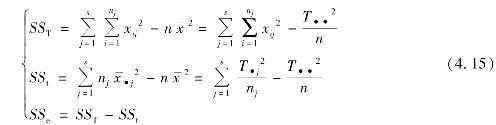
例4.3 如上所述,在例4.1中,试取α=0.05,完成这一假设检验。
解 s=4,n1=7,n2=5,n3=8,n4=6,则n=26
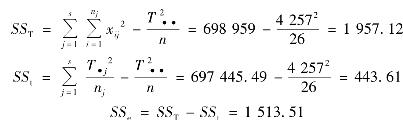
得方差分析表,见表4.5。
表4.5 方差分析表
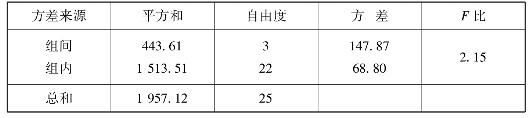
因
F(3,22)=2.15<F0.05(3,22)=3.05
可认为4种玻璃瓶试样的热疲劳性无显著差异。
例4.4 如上所述,在例4.2中,试取α=0.05,α=0.01,完成这一假设检验。
解 s=6,n1=n2=…=n6=4,则

得方差分析表,见表4.6。
表4.6 方差分析表
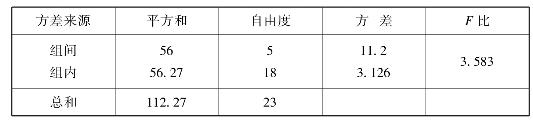
又
F0.05(5,18)=2.77,F0.01(5,18)=4.25
由于
4.25=F0.01(5,18)>F(5,18)=3.58>F0.05(5,18)=2.77
故浸泡水的温度对缩水率有显著影响,但不能说有高度显著的影响。
本节的方差分析是在这两项假设下,检验各个正态总体均值是否相等:一是正态性假设,假定数据服从正态分布;二是等方差性假设,假定各正态总体方差相等。由大数定律及中心极限定理,以及多年来的方差分析应用,知正态性和等方差性这两项假设是合理的。
4.1.2 双因素试验的方差分析
在许多实际问题中,往往要同时考虑两个因素对试验指标的影响。例如,进行某一项试验,当影响指标的因素不是一个而是多个时,要分析各因素的作用是否显著,就要用到多因素的方差分析。本节就两个因素的方差分析作一简介。当有两个因素时,除每个因素的影响之外,还有这两个因素的搭配问题。见表4.7中的两组试验结果,都有两个因素A和B,每个因素取两个水平。
表4.7a
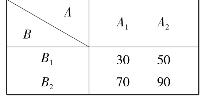
表4.7b
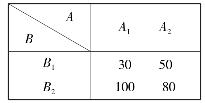
表4.7a中,无论B在什么水平(B1还是B2),水平A2下的结果总比A1下的高20;同样的,无论A是什么水平,B2下的结果总比B1下的高40。这说明A和B单独地各自影响结果,互相之间没有作用。
表4.7b中,当B为B1时,A2下的结果比A1的高,而且当B为B2时,A1下的结果比A2的高;类似地,当A为A1时,B2下的结果比B1的高70,而A为A2时,B2下的结果比B1的高30。这表明A的作用与B所取的水平有关,而B的作用也与A所取的水平有关。即A和B不仅各自对结果有影响,而且它们的搭配方式也有影响。把这种影响称为因素A和B的交互作用,记作A×B。在双因素试验的方差分析中,不仅要检验水平A和B的作用,还要检验它们的交互作用。
1)双因素等重复试验的方差分析
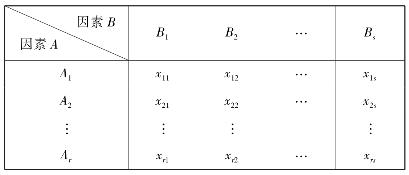
设有两个因素A,B作用于试验的指标,因素A有r个水平A1,A2,…,Ar,因素B有s个水平B1,B2,…,Bs,现对因素A,B的水平的每对组合(Ai,Bj),i=1,2,…,r;j=1,2,…,s都做t(t≥2)次试验(称为等重复试验),得到表4.8的结果。
表4.8 等重复试验结果

类似于单因素情况,对这些问题的检验方法也是建立在平方和分解上的。
记
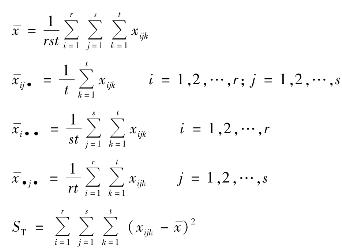
平方和的分解式为
S T=S E+SA+SB+SA×B (4.16)
其中
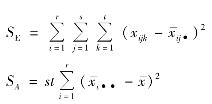

式中 S E——误差平方和;
SA,SB——因素A,B的效应平方和;
SA×B——A,B交互效应平方和。
可得出双因素试验的方差分析表4.9。
表4.9 双因素试验的方差分析表

当给定显著性水平α后,根据:
FA≥Fα(r-1,rs(t-1))得测试结果为:因素A影响显著。
FB≥Fα(s-1,rs(t-1))得测试结果为:因素B影响显著。
FA×B≥Fα(r-1)(s-1),rs(t-1))得测试结果为:因素A×B影响显著。
完成显著性分析。
在实际中,与双因素方差分析类似可按以下较简便的公式来计算S T,SA,SB,SA×B,S E:
记
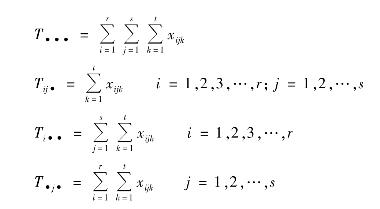
即有
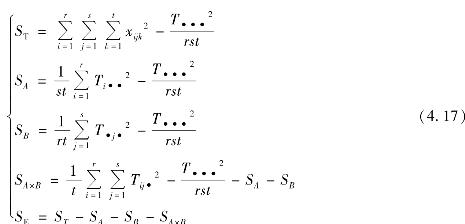
例4.5 用不同的生产方法(不同的硫化时间和不同的加速剂)制造的胶体的抗牵拉强度(以kg/cm2为单位)的观察数据见表4.10。试在显著水平0.10下分析不同的硫化时间(A)、加速剂(B)以及它们的交互作用(A×B)对抗牵拉强度有无显著影响。
表4.10 胶体的抗牵拉强度观察数据
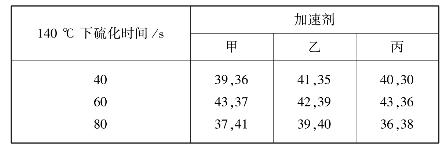
解 按题意,r=s=3,t=2,T…,Tij.,Ti..,T.j.的计算见表4.11。
表4.11 数据计算表
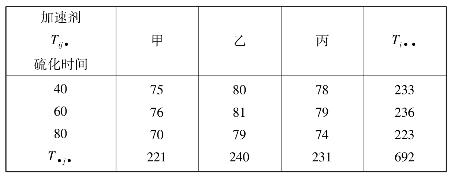
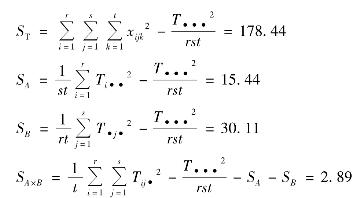
S E=S T-SA-SB-SA×B=130
得方差分析表,见表4.12。
表4.12 方差分析表
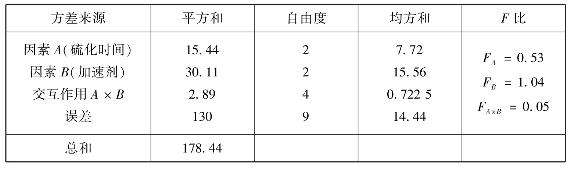
由于
F0.10(2,9)=3.01>FA,F0.10(2,9)=3.01>FB,F0.10(4,9)=2.69>FA×B
因此,硫化时间、加速剂以及它们的交互作用对胶体的抗牵拉强度的影响不显著。
2)双因素无重复试验的方差分析
在双因素试验中,如果对每一对水平的组合(Ai,Bj)(i=1,2,…,r;j=1,2,…,s)只作一次试验,即不重复试验,所得结果见表4.13。
表4.13 无重复试验结果
记
![]()
平方和分解公式为
S T=S E+SA+SB (4.18)
其中
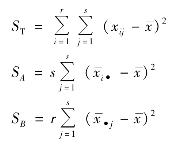
![]()
分别为总平方和、因素A,B的效应平方和和误差平方和。
得方差分析表,见表4.14。
表4.14 方差分析表

当给定显著性水平α后,根据:
FA≥Fα((r-1),(r-1)·(s-1))得测试结果为:因素A影响显著。
FB≥Fα((s-1),(r-1)·(s-1))得测试结果为:因素B影响显著。
例4.6 测试品牌白酒不同酒精含量在各种温度下的挥发值,表4.15列出了试验的数据,问试验温度、酒精含量对白酒的挥发值的影响是否显著?(α=0.01)
表4.15 白酒的挥发值实验数据
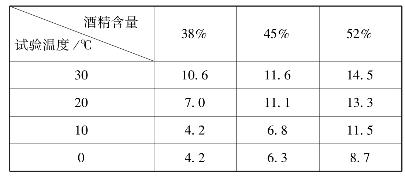
解 由已知,r=4,s=3,经计算得方差分析表,见表4.16。
表4.16 方差分析表
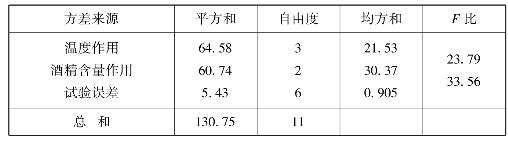
由于
F0.01(3,6)=9.78<FA,F0.01(2,6)=10.92<FB
结果表明,试验温度、酒精含量对白酒的挥发值影响是显著的。
案例分析与讨论题
1.某一工艺参数分4个水平进行单因素试验,每个水平重复试验3次,试验结果见表4.17。试判断因素对指标影响的显著性。
表4.17 试验结果
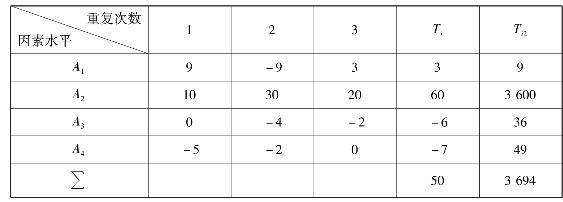
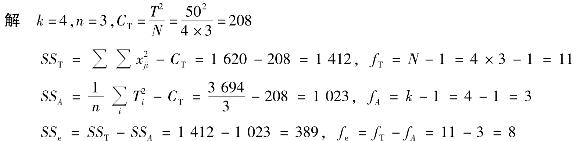
得方差分析表,见表4.18。
表4.18 方差分析表
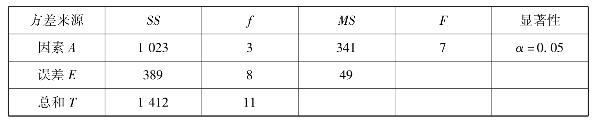
因此,得
F0.05(3,8)=4.07
由此可知,工艺参数高到达显著水平。
2.某一食品的生产设备分5个水平进行单因素试验,每个水平重复试验5次,试验结果见表4.19。试判断因素对指标影响的显著性。
表4.19 试验原始数据
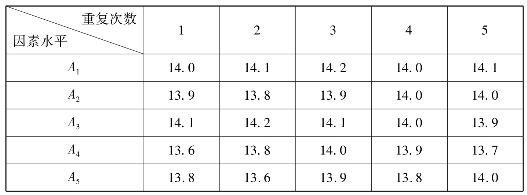
解 方差分析表见,见表4.20。
表4.20 方差分析表
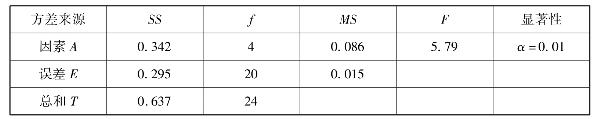
因此,得
F0.01(4,20)=4.43
由此可知,几台设备产量差异高度显著。
3.某一食品的生产量主要由生产时的室内温度和工作人员的熟练程度所决定,实验在5个不同温度(因素A)和3个不同工作人员(因素B)的条件下完成,试验结果见表4.21。试判断因素对指标影响的显著性。
表4.21 试验结果

解 方差分析表见表4.22。
表4.22 方差分析表
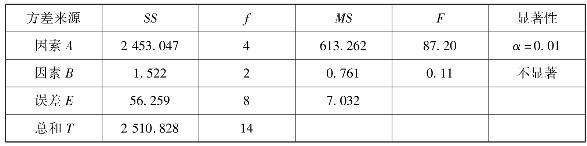
因此,得
F0.01(4,8)=7.01,F0.1(2,8)=3.11
由此可知,温度的影响高度显著,试验人员间无差异。
反思与练习
1.研究6种氮肥施用法对小麦的效应,每种施肥法种5盆小麦,完全随机设计(见表4.23)。最后测定它们的含氮量(mg),试作方差分析。
表4.23

2.某水产研究所为了比较4种不同配合饲料对鱼的饲喂效果,选取了条件基本相同的鱼16尾,随机分成4组,投喂不同饲料,经一个月试验以后,各组鱼的增重结果列于表4.24。
表4.24
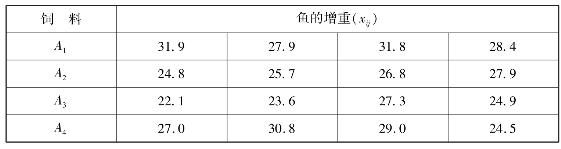
试检验不同配合饲料对鱼的饲喂效果是否有显著影响(取α=0.05)?运算结果要求列出方差分析表,并给出检验结论。
3.用生长素处理豌豆,共6个处理。豌豆种子发芽后,移植24株,分成4组,每组6个木箱,每箱1株1个处理。试验共有4组24箱,试验时按组排列于温室中,使同组各箱的环境条件一致。然后记录各箱见第一朵花时4株豌豆的总节间数,其结果见表4.25。
试检验5种药剂对豌豆总节间数影响有无显著差异(取α=0.05)。
表4.25

任务4.2 一元回归分析
4.2.1 相关分析
1)变量关系的类型
在大量变量关系中,存在着两种不同的类型:函数关系和相关关系。
函数关系是指变量之间存在的一种完全确定的一一对应的关系,它是一种严格的确定性的关系。
相关关系是指两个变量或者若干变量之间存在着一种不完全确定的关系,它是一种非严格的确定性的关系。
两者之间的联系如下:
①由于人类的认知水平的限制,有些函数关系可能目前表现为相关关系。
②对具有相关关系的变量进行量上的测定需要借助于函数关系。
2)相关关系的种类
相关关系的种类如图4.1所示。

3)相关分析的内容
对于相关关系的分析可借助于若干分析指标(如相关系数或相关指数)对变量之间的密切程度进行测定,这种方法通常被称作相关分析(狭义概念)。广义的相关分析还包括回归分析。对于存在的相关关系的变量,运用相应的函数关系来根据给定的自变量来估计因变量的值,这种统计分析方法通常称为回归分析。相关分析和回归分析都是对现象之间相关关系的分析。广义相关分析包括的内容如图4.2所示。

4)相关关系密切程度的测定
在判断相关关系密切程度之前,首先确定现象之间有无相关关系。确定方法有:一是根据自己的理论知识和实践经验综合分析判断;二是用相关图表进一步确定现象之间相关的方向和形式。在此基础上,通过计算相关系数或相关指数来测定相关关系密切的程度。相关系数是用来说明直线相关的密切程度;相关指数则是用来判断曲线相关的密切程度。这是主要介绍相关系数的计算。
相关系数是用来分析判断直线相关的方向和程度的一种统计分析指标,其计算方法中最简单、最常用的为积差法,是用两个变量的协方差与两变量的标准差的乘积之比来计算的,计算公式为
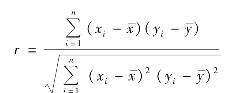
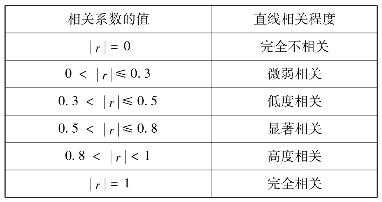
相关系数的取值范围是:-1≤r≤1正的表示正相关,负的表示负相关。利用相关系数判断相关关系的密切程度,见表4.26。
表4.26 利用相关系数判断相关关系的密切程度
4.2.2 一元线性回归分析
1)回归分析的基本概念
客观世界中普遍存在着变量间的关系,而变量间的关系一般可分为两类:确定性关系和非确定性关系。
确定性关系:可用函数来表示的变量间关系。
非确定性关系:不能用函数来表示的变量间关系,也称为相关关系或统计关系。例如,身高与体重之间的关系。一般来说,人高一些,体重要重一些,但同样身高的人,体重往往不相同。又如,人的血压与年龄之间的关系,树高与生长时间之间的关系,以及商品的销售量与单价之间的关系等都是相关关系。
按照所研究的变数在图形上表现出来的特点,将回归与相关分为直线回归和直线相关与曲线回归和曲线相关两种类型:如两个变数之间的关系大体表现为直线关系的为直线回归和直线相关;两个变数之间的关系可用曲线来描述的是曲线回归和曲线相关。本章将讨论有一定联系的两个变数的直线回归与直线相关的有关问题。
对于具有一定联系的两个变数,可分别用变数符号y和x表示。对具有统计关系的两个变数的资料进行初步考察的简便而有效的方法是画出资料的散点图(scatter diagram),也就是将这两个变数的n对观察值(x1,y1),(x2,y2),…,(xn,yn)分别以坐标点的形式标记于同一平面直角坐标系中,获得散点图。根据散点图可初步判定两个变数x和y之间的关系,如图4.3所示。
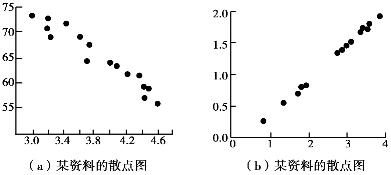
图4.3 资料的散点图
对具有相关关系的两个变数,统计分析的任务是由试验数据推算得一个表示y随x的改变而改变的方程式y^=f(x)(regression equation of y on x),式中y^表示由该方程估得在给定x时的理论y值,方程式y^=f(x)为回归方程式,以计算回归方程为基础的统计分析方法称为回归分析(regression analysis)。回归分析是指通过试验和观测去寻找隐藏在变量间相关关系的一种数学方法,是研究变量间相关关系的一种有力的数学工具。
例4.7 为研究某一化学反应过程中,温度x(℃)对产品得率y(%)的影响,测得数据见表4.27。
表4.27 某化学反应测的数据

这里自变量x是普通变量,y是随机变量。画出散点图如图4.4所示。
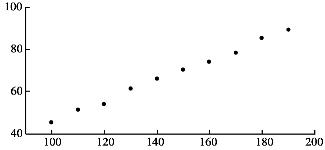
图4.4 散点图
由图4.4可知,随着温度x的增加,产品得率y也增加,且这些点(xi,yi)(i=1,2,…,10)近似在一条直线附近,但又不完全在一条直线上。引起这些点(xi,yi)与直线偏离的原因有两个:一是本身温度和产品得率存在的内在关系;二是在温度xi下观察产品得率存在着一些不可控制的因素。
这样可把观测结果y看成是由两部分叠加而成的:一部分是由x的线性函数引起的,记为a+bx,其中a,b还需要估计;另一部分是由随机因素引起的,记为ε,即
y=a+bx+ε (4.19)
这就是一元回归方程模型。
2)一元线性回归方程
在式(4.19)中x是一般变量,它可以精确测量或加以控制,y是可观测其值的随机变量,a,b是未知参数,ε是不可观测的随机变量。
通过观测,获得了n组独立的观测数据(xi,yi),i=1,2,…,n,当由观测值获得未知参数a,b的估计a^,b^后,得到的方程
y^=a^+b^x (4.20)
称为y^关于x的一元线性回归方程。
式(4.20)读作“y依x的直线回归方程”,其中x是自变数;y^是和x的量相对应的依变数的点估计值;a^叫回归截距(regression intercept),是x=0时的y^值,即回归直线在y轴上的截距;b^叫回归系数(regression coefficient),是x每增加一个单位数时,y^平均地将要增加(b^>0时)或减少(b^<0时)的单位数。
下面的任务是对a、b的估计:取x的n个不全相同的取值x1,x2,…,xn,作n次独立试验,得到观测值
(x1,y1),(x2,y2),…,(xn,yn) (4.21)
利用最小二乘法,经过计算可得
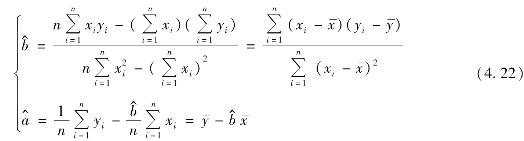
其中
![]()
为了计算上的方便,引入记号
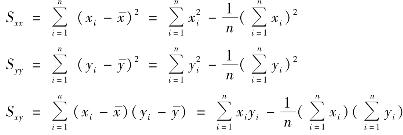
这样,a和b的估计值可写为

例4.8 求例4.7中变量y关于x的线性回归方程。
解 n=10,经计算得
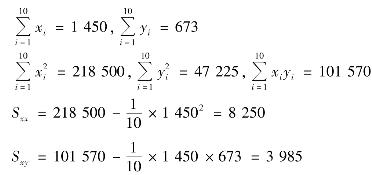
故得
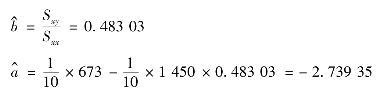
于是,得到回归直线方程
y^=-2.739 35+0.483 03x
上述直线回归方程中的意义为:温度每升高1°,产品得率约提高0.48%。
3)一元线性回归方程的显著性检验
在以上的讨论中,假如x和y变数总体并不存在直线回归关系,那么随机抽取的一个样本用上述方法也能算得一个直线方程y^=a^+b^x。显然,这样的回归方程是靠不住的。因此,对于样本的回归方程,应测定其来自无直线回归关系总体的概率大小,只有当这种概率小于0.05 或0.01时,才能冒较小的危险确认其所代表的总体存在着直线回归关系。对于回归关系的显著性测验,通常采用t测验和F测验。
t测验的过程如下:
记
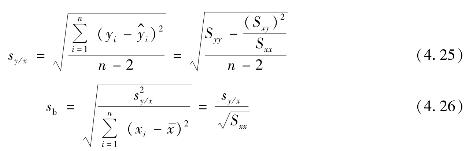
式中 sy/x——回归估计标准误;
s b——回归系数标准误。
①规定显著水平:α=0.05或α=0.01。
②测验计算:计算t值,其计算公式为
![]()
③推断:计算出样本回归系数的t值后,与t值表中的tα相比较,以确定样本的t值在t分布中出现的概率。此t值遵循ν=n-2的t分布。如果:
t <t0.05,P>0.05,即可认为该样本回归方程是其来自于无显著直线回归关系的总体。
t0.05< t <t0.01,P<0.05,即认为该回归方程是来自于有显著直线回归关系的总体。
t >t0.01,P<0.01,即认为该回归方程是来自于有极显著直线回归关系的总体。
F测验的过程如下:
记
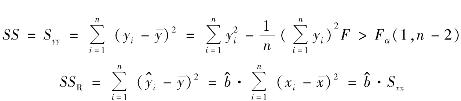

称SS为总偏差平方和,称SS E为残差平方和,称SS R为回归平方和。
平方和分解公式为
SS=SS E+SS R (4.28)
则有方差分析表,见表4.28。
表4.28 方差分析表(一元正态线性模型)

若F取的值较大时,表示SS R相对较大,而SS E相对较小,即y与x的线性关系起主导作用,可认为x与y之间有线性关系;若F取的值较小时,则SS R相对较小,而SS E相对较大,即随机误差起主导作用,说明x与y之间没有线性关系。
因此,在显著性水平α下,由
F>Fα(1,n-2)
即认为回归效果显著,即回归方程是有意义的。
例4.9 检验例4.8中回归方程的回归效果是否显著,取α=0.05。解 由例4.8和例4.9可知b^=0.483 03,Sxx=8 250,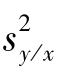 =0.9,故
=0.9,故
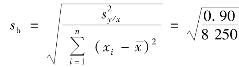
则
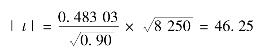
查表得
t0.05/2(n-2)=t0.025(8)=2.306 0
因为|t|=46.25>2.306 0,认为回归效果是显著的。
案例分析与讨论题
有一试验,其参数x与指标y的对应关系见表4.29,试进行一元线性回归分析。
表4.29
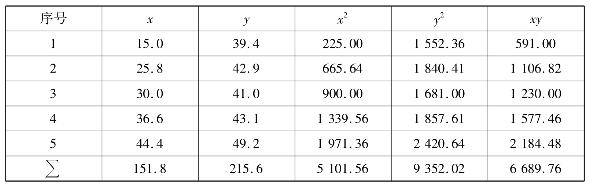
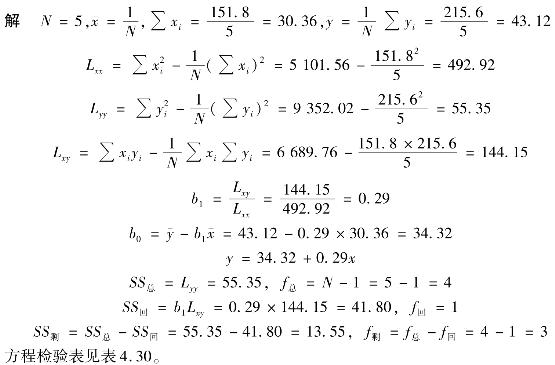
表4.30

因此得
F0.1(1,3)=5.54
反思与练习
1.抽取由10名大学生组成的随机样本,研究他们在高中与大学的英语成绩得出表4.31的结果。
表4.31

试用相关系数r测定其相关程度。
2.表4.32是几家百货商店销售额和利润率的资料,试进行一元线性回归分析。
表4.32
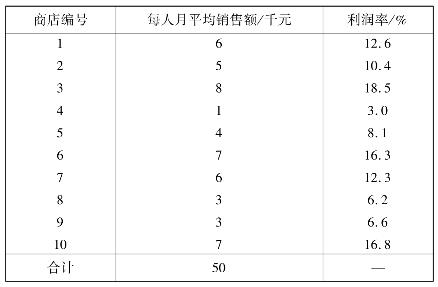
任务4.3 优选法
关于最佳点的选择问题,通常称为选优问题。
在实践中,人们往往通过做实验的方法来寻找各种因素的最佳点,这种方法称为试验方法。
在实践中的许多情况下,试验结果与因素的关系,要么很难用数学形式来表达,要么表达式很复杂,优选法与试验设计是解决这类问题的常用的数学方法。
优选法就是根据生产和科研中的不同问题,利用数学原理,合理安排试验,以求迅速找到最佳点的科学的试验方法。
试验设计也是一种运用数学原理进行实验的方法,它是考虑在多因素的情况下,如何帮助人们通过较少的试验次数得到较好的因素组合,形成较好的试验方案。
4.3.1 单因素优选法
1)均分法
均分法是在试验范围[a,b]内,根据精度要求和实际情况,均匀地排开试验点,在每一个试验点上进行试验,并相互比较,以求得最优点的方法。做法:如试验范围L=b-a,试验点间隔为N,则试验点n为(包含两个端点)
![]()
例4.10 对采用新工艺的玻璃瓶进行磨削加工,砂轮转速范围为420~720 r/min,拟经过试验找出能使光洁度最佳的砂轮转速值。
解 N=30 r/min
![]()
故试验转速为420,450,480,510,540,570,600,630,660,690,720 r/min。
2)0.618法(黄金分割法)
黄金分割法是在试验范围[a,b]内,首先安排两个试验点,再根据两点试验结果,留下好点,去掉不好点所在的一段范围,再在余下的范围内寻找好点,去掉不好的点,如此继续地做下去,直到找到最优点为止。
在分数法中, 的值可随着n的增大而接近0.618,因此在没有明确要求试验次数或可进行较多次数的试验时,每次试验都选取黄金分割点(取值为0.618的点)和其对称点0.382进行试验。对两者试验结果进行比较,如果0.618好于0.382,舍去区间[0,0.382],否则舍去区间[0.618,1],无论去掉哪一个区间,都得到一个新的区间,总有一个试验点留在这个区间中。再在其对称点处做试验,依次下去,可以用最少的次数得到满意的结果。
的值可随着n的增大而接近0.618,因此在没有明确要求试验次数或可进行较多次数的试验时,每次试验都选取黄金分割点(取值为0.618的点)和其对称点0.382进行试验。对两者试验结果进行比较,如果0.618好于0.382,舍去区间[0,0.382],否则舍去区间[0.618,1],无论去掉哪一个区间,都得到一个新的区间,总有一个试验点留在这个区间中。再在其对称点处做试验,依次下去,可以用最少的次数得到满意的结果。
分数法和0.618法都是先做两次试验,再通过比较,找出最好点所在的位置的范围。通过这种方法来不断地将试验范围缩小,最后找到最佳点。
0.618法的做法:如图4.5所示,第一个试验点x1设在范围[a,b]的0.618位置上,第二个试验点x2取成x1的对称点,则
x1=(大-小)×0.618+小=(b-a)×0.618+a (4.29)
x2=(大+小)-第一点(即前一点)=(b+a)-x1 (4.30)
![]()
图4.5
第三个试验点的安排有以下3种情形:
①x1是好点,则划去[a,x2],保留[x2,b]。x1的对称点x3,在x3安排第三次试验(见图
4.6)。
![]()
图4.6
x3=大+小-前一点=b+x2-x1 (4.31)
②x2是好点,则划去[x1,b],保留[a,x1]。第三个试验点x3应是好点x2的对称点(见图4.7)。
![]()
图4.7
x3=大+小-前一点=x1+a-x2 (4.32)
③如果f(x1)和f(x2)一样,则应该具体分析,看最优点可能在哪边,再决定取舍。一般情况下,可同时划掉[a,x2]和[x1,b],仅留中间的[x2,x1],把x2看成新a,x1看成新b,然后在范围[x2,x1]内0.382,0.618处重新安排两次试验。
无论何种情况,在新的范围内,又有两次试验可以比较。根据试验结果,再去掉一段或两段试验范围,在留下的范围中再找好点的对称点,安排新的试验。
这个过程重复进行下去,直到找出满意的点,得出比较好的试验结果;或者留下的试验范围已很小,再做下去试验差别不大时也可终止试验。
例4.11 炼某种合金钢,需添加某种化学元素以增加强度,加入范围为1 000~2 000 g。求最佳加入量。
解 第一步,先在试验范围长度的0.618处做第一个试验,试验点由式(4.37)计算,即x1=(大-小)×0.618+小=a+(b-a)×0.618=1 000 g+(2 000 g-1 000 g)×0.618=1 618 g
第二步,第二个试验点由式(4.38)计算,即
x2=大+小-第一点=2 000 g+1 000 g-1 618 g=1 382 g x1=1 618克,x2=1 382 g
第三步,比较第一与第二两点上所做试验的效果,现在假设第一点比较好,就去掉第二点,即去掉[1 000,1 382]=那一段范围。留下[1 382,2 000],则
x3=大+小-第一点=1 382 g+2 000 g-1 618 g=1 764 g
第四步,比较在上次留下的好点,即第一处和第三处的试验结果,看哪个点好,然后就去掉效果差的那个试验点以外的那部分范围,留下包含好点在内的那部分范围作为新的试验范围,……如此反复,直到得到较好的试验结果为止。
可知,每次留下的试验范围是上一次长度的0.618倍,随着试验范围越来越小,试验越趋于最优点,直到达到所需精度即可。
3)对分法
对分法是适用于试验范围[a,b]内,目标函数为单调(连续或间断)的情况下,求最优点的方法。每次选取因素所在试验范围[a,b]的中点处C做试验。
根据试验结果,如下次试验在高处(取值大些),就把此试验点(中点)以下的一半范围划去;如下次试验在低处(取值小些),就把此试验点(中点)以上的一半范围划去。每试验一次,试验范围缩小一半,重复做下去,直到找出满意的试验点为止。
例4.12 蒸馒头究竟放多少碱合适(碱少会酸,碱多会发黄有碱味)?
首先估计用碱量的范围,如4份到12份。第一次在4~12份的中点8份处做一次试验,如果蒸出来的馒头发酸,说明碱放少了。第二次就在8~12份的中点10份处做第二次试验,结果馒头不酸,但发黄,说明碱放多了。第三次就在8~10份的中点9份处做试验,如果蒸出来的馒头合适,则碱量就定在9份。
概括来说,上述方法就是先确定试验范围,第一次取其中点,视其大小决定取舍区间。在保留的区间内再取中点,再看其大小决定取舍区间,这样继续下去就可找到所要求的点。
4)分数法
在试验次数给定的情况下,分数法是解决单因素问题的最优方法。
下面以3次试验为例。
分数法的做法:所有可能的试验总数正好是某个Fn-1:
第一步,前两个试验点放在试验范围的Fn-1,Fn-2的位置上,也就是先在第Fn-1,Fn-2点上做试验(见图4.8)。
![]()
图4.8
比较这两个试验的结果,如果第Fn-1点好,划去第Fn-2点以下的试验范围;如果第Fn-2点好,划去Fn-1点以上的试验范围。
第二步,在留下的试验范围中,还剩下Fn-1-1个试验点,重新编号,其中第Fn-2和Fn-3个分点,有一个是刚好留下的好点,另一个是下一步要做的新试验点,两点比较后同前面的做法一样,从坏点把试验范围切开,短的一段不要,留下包含好点的长的一段,这时新的试验范围就只有Fn-2-1个试验点。
第三步,以后的试验按照上面的步骤重复进行,直到试验范围内没有更好的为止。
例4.13 假设某混凝沉淀试验,所用的混凝剂为某阳离子型聚合物与硫酸铝,硫酸铝的投入量恒定为10 mg/L,而某阳离子聚合物的可能投加量分别为0.10,0.15,0.20,0.25,0.30 mg/L。试利用分数法来安排试验,确定最佳阳离子型聚合物的投加量。
解 根据题意可知,可能的试验总次数为5次。由裴波那契数列可知,有
F5-1=8-1=7
F4-1=5-1=4
故
F4-1=4<5<F5-1=7
①首先需要增加两个虚设点,使其可能的试验总次数为7次,虚设点可安排在试验范围的一端或两端。假设安排在两端,即一端一个虚设点。
②第一个试验点选在第5个分点0.25 mg/L;第二个试验点在第3个分点0.15 mg/L。假设1点好,划去3分点以下的,再重新编号。
③1点和3点比较,假设3点好,划去2分点以下的,再重新编号。
④此时第四个试验点为虚设点,直接认定它的效果比3点差,即3点好。试验结束,定下该阳离子型聚合物的最佳投加量为0.30 mg/L。
4.3.2 双因素优选法
1)对开法
两因素时,假设优选范围为长方形,即
a<x<b,c<y<d
在此长方形的纵横两根中线x=(a+b)/2,y=(c+d)/2上用单因素方法求出最优点P 和Q。如果Q较大,去掉x<(a+b)/2部分,否则去掉另一半,逐步得到所需结果,如图4.9所示。
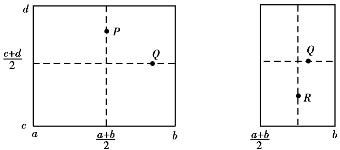
图4.9
例4.14 某化工厂试制磺酸钡,其原料磺酸是磺化油经乙醇水溶液萃取出来的,试验目的是选择乙醇水溶液的合适浓度和用量,使分离出的磺酸最多。根据经验,乙醇水溶液浓度变化范围为50%~90%(体积百分比),用量范围为30%~70%(质量百分比)。
做法:先横向对折,即将乙醇用量固定在50%,用单因素的0.618法选取最优浓度为80%(见图4.7(a))的点A。而后纵向对折,将浓度固定在70%,用0.618法对用量进行优选,结果是点B较好。比较点A与点B的试验结果,点A比点B好,于是丢掉试验范围下边的一半。在剩下的范围内再上下对折,将浓度固定在80%,对用量进行优选,结果不如点A好,于是找到了好点,即点A,试验至此结束(见图4.10)。
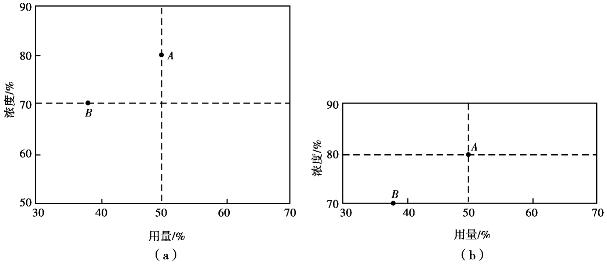
图4.10
2)旋升法
优选范围:一矩形,即
a<x<b,c<y<d
做法:先在一条中线,如x=(a+b)/2上,用单因素法求得最大值,假定在P1点取得最大值,然后过P1点作水平线,在这条水平线上进行单因素优选,找到最大值,假定在P2处取得最大值,这时应去掉通过P1点的直线所分开的不含P2点的部分;又通过P2点的垂线上找最大值,假定在P3处取得最大值,此时应去掉P2的上部分,继续找下去,直到找到最佳点(因素的先后顺序按各因素对试验结果影响的大小顺序)。
优选方法如图4.11所示。
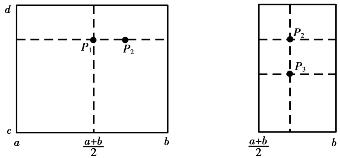
图4.11
3)平行线法
在实际问题中,经常会遇到由于设备或其他种种条件的限制而有一个因素不容易调整。例如,一个是浓度,一个是流速,调整浓度就比调整流速困难。在这种情形下,采用平行线法比较优越。
这个方法是:把不易调整的一个因素固定在某个位置,对易于调整的另一个因素进行优选,比较结果,得到最好点。
优选范围为
a<x<b,c<y<d
优选方法是:先将y固定在范围[c,d]的0.618处用单因素法找最大值,假定在P点取得这一值,再把y固定在范围[c,d]的0.382处,用单因素法找到最大值,假定在Q点取得该值。如果P>Q则去掉Q点下面的部分,否则去掉P点上面的部分,再用同样的方法处理余下的部分。
优选方法如图4.12所示(设:x易调整,y不易调整)。
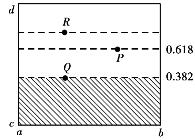
图4.12
4)按格上升法
首先将所考虑的区域画上格子,然后采用与上述3种方法类似的过程进行优选,但用分数法代替黄金分割法。
例4.15 优选的范围是一个21×13的格子图,先在x=13的直线上用分数法做5次试验,又在y=8的直线上也用分数法,这时T点已做过试验,因此只需做5次试验,各得一个最优点,分别记为P,Q。如果Q>P,则留下8×13的格子,在余下的范围内采用同样的方法进行优选。
在试验区域画上格子,将分数法与上述方法结合起来,如图4.13所示。
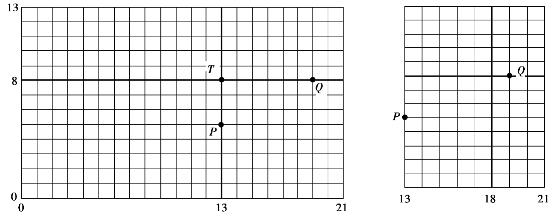
图4.13
5)翻筋斗法
从一个等边三角形ABC出发,在3个顶点各做一次试验。如果C点所做的试验好,则作C点的对顶同样大的三角形CDE,在DE点做试验,如果D点好则再作D点的对顶三角形直到找到最优点,如图4.14所示。
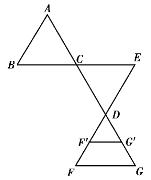
图4.14
案例分析与讨论题
1.用0.618法确定最佳点时,试验区间为[2,4],若第一个试点x1处的结果比第二个试点x2处的结果好,且x1>x2,则求存优区间。
解 依题意,得
x1=2+0.618×(4-2)=3.236
x2=2+4-3.236=2.764
得存优区间为[2.764,4]。
2.某食品工厂准备对一新产品进行技术改良,现决定优选加工温度,试验范围定为60~80℃,精确度要求±1℃,现在技术员用分数法进行优选。
①如何安排试验?
②若最佳点为69℃,请列出各试验点的数值。
③要通过多少次试验可以找出最佳点?
解 ①试验区间为[60,81],等分为21段,分点为61,62,…,79,80,因此
60+13/21×(81-60)=73℃
故第一试点安排在73℃,由“加两头,减中间”的方法得
60+81-73=68
因此第二试点选在68℃。后续试点可以用“加两头,减中间”的方法来确定。
②若最佳点为69℃,即从第二次试验开始可知,69℃在存优范围内,由实验安排可知,第一、第二次试点的值分别为73,68,因为69∉[60,68],故去掉68℃以下的部分,则第三次试验点的值为
68+81-73=76
同理,去掉76℃以上的部分,第四次试验点的值为
68+76-73=71
第五次试验点的值为
68+73-71=70
第六次试验点的值为
68+71-70=69
即安排了6次试验,各试验点的数值依次为73,68,76,71,70,69。
③共有20个分点,由分数法的最优性定理及F6+1-1=20可知,通过6次试验可从这20个分点中找出最佳点。
3.某炼油厂试制磺酸钡,其原料磺酸是磺化油经乙醇水溶液萃取出来的,试验目的是选择乙醇水溶液的合适浓度和用量,使分离出来的白油最多。根据经验,乙醇水溶液浓度变化范围为50%~90%(体积百分比),用量变化范围为30%~70%(质量百分比),精度要求为5%。试用纵横对折法对工艺条件进行优选。
解 由题意设影响该试验结果的因素Ⅰ为浓度,试验范围为50%~90%;因素Ⅱ为用量,试验范围为30%~70%。
试验:①先固定浓度在中点(50%+90%)/2=70%处,对用量进行单因素优选,得最佳点A1。
同样,将用量固定在中点(30%+70%)/2=50%处,对浓度进行单因素优选,得最佳点B1。比较A1和B1的试验结果,如果A1比B1好,则沿坏点B1所在的线,丢弃不包括好点A1所在的半个平面区域,即丢弃平面区域为
50%≤Ⅰ≤90%, 50%≤Ⅱ≤70%
②然后再在因素Ⅱ的新范围即[30%,50%]内取中点40%,用单因素方法优选因素Ⅰ,得最佳点为B2。如此继续下去,不断地将试验范围缩小,直到找到满意的结果为止。
反思与练习
1.对某一单因素优选试验,已知目标函数为单峰函数,试验范围为[0,100],用黄金分割法进行优选,试验结果为试验点1的结果比2点好,试验点3的结果比点1好,试验点3的结果比4点好。试用黄金分割法对称公式计算出4个试验点的试验条件。
2.在食品的加工工艺条件的试验中,要考虑3个因素:原料用量、反应温度、反应时间,这是一个3因素3水平的问题。根据过去积累的实际经验确定了它们的变化范围:
A.原料用量(kg) A1=840,A2=850,A3=860
B.反应温度(℃) B1=15,B2=20,B3=25
C.反应时间(min) C1=40,C2=60,C3=80
如果所有的试验都要做,共需多少次试验?
3.调酒师为了调制一种鸡尾酒,每100 t烈性酒中需要加入柠檬汁的量为1 000~2 000 g,现准备用黄金分割法找到它的最优加入量。
①写出这个试验的操作流程。
②如果加入柠檬汁误差不超出1 g,问需要多少次试验?
4.阿托品是一种抗胆碱药,为了提高产量、降低成本,利用优选法选择合适的脂化工艺条件。根据分析,主要因素为温度与时间,定出其试验范围为温度:55~75℃,时间:30 min~210 min。用从好点出发法对工艺条件进行优选:参照生产条件,先固定温度为55℃,用单因素法优选时间,得最优时间为A:150 min;再固定时间为150 min,用单因素法优选温度,得最优温度为B:67℃;再固定温度为67℃,用单因素法再优选时间,得最优时间为C:80 min;再固定时间为80 min,又对温度进行优选,结果还是67℃好。试问实际中采用这个工艺进行生产,平均产率提高了多少?
任务4.4 正交试验法
4.4.1 正交试验概述
1)正交表的特点
正交表代号L a(bc)的含义:a为正交表行数,即试验点数;b为各因素水平数,c为正交表列数,每一列可安排一个因素,见表4.33。
表4.33 L4(23)正交表
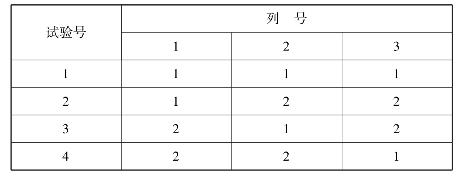
正交的含意:若将表4.33中2换成-1,则任一列之和为0,任两列乘积的和为0。若将列看作向量,则两向量垂直相交,即正交。
从试验点的空间分布可知,L4(23)正交表为 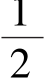 实施。
实施。
①均衡搭配。即任一因素的任一水平与其他因素的每一水平相遇的次数均等。
②综合可比。即任一因素的各水平出现的次数相等。
2)交互作用表
(1)交互列的位置
交互列的位置要查交互列表(见表4.34)。
表4.34 L8(27)正交表
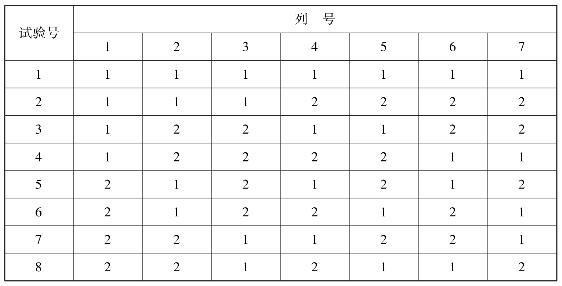
(2)混杂
若在交互两因素的交互列上,安排其他因素或其他因素的交互,则在此列将出现混杂现象。
(3)如何对待混杂
①若不想用较多的试验,则就可能有混杂,此时要用专业经验来判断。
②若不研究规律,只找出参数较优组合,则可不考虑混杂。
3)试验方案设计
(1)列因素水平表
列因素水平表见表4.35。
表4.35 因素水平表
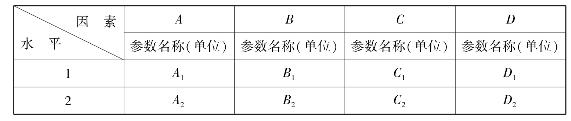
(2)选正交表
选正交表的原则:正交表的列数应≥要考察的因素和交互作用个数的最小正交表。
(3)表头设计
表头设计即因素放在哪一列。其原则如下:
①若不考虑交互作用,则因素随机放各列,但若有余列时,因素最好不要放在其他因素的交互列上,一则避免混杂,二则可看出交互作用的大小。
②若要考虑交互作用,则应先排要交互的因素,其他因素按不混杂的原则随机排列。
(4)列出试验方案
将表中字码换成对应的水平值。每一行的因素水平组合即为一个试验点。
4)试验
试验应注意以下3点:
①各因素的水平组合方案不能变。
②试验点的实施顺序是随机的,即可根据水平改变的难易来安排。
③严格控制试验条件,减少试验误差。
4.4.2 正交试验数据的直观分析法
1)单指标试验数据的极差分析
(1)分析的内容
①找出因素对指标影响的主次。
②找出各因素的较优水平,即取哪个水平最好。
③找出参数的较优组合,即各因素取何水平搭配起来最好,考虑了交互作用。(2)分析的步骤
①算出各因素同一水平的指标和km与均值km= ,m=1~b。
,m=1~b。
②由各水平的均值算出极差R=k max-k min。
③找出各因素的较优水平:指标好的水平为较优水平,事先要知道指标是越高越好还是越近越好。
④根据极差R的大小确定因素的主次,即对指标影响的大小,R越大影响越显著。
⑤若考察交互作用时,要找出优搭配(水平搭配)。
⑥找出因素水平的较优组合,即参数的较优组合(在试验中可能出现,也可能不出现)。
(3)注意事项
①若交互作用比其中某一因素的影响大时,应先从交互中找出因素主次和较优水平。
②对于空列,反映了试验误差,若恰为某两因素的交互作用列,且该列极差很大,则该交互作用不能忽略。
例4.16 豇豆脱水正交试验设计。以干制品中Vc含量为指标,Vc含量越高越好。研究3个因素,每因素取2水平。因素水平编码见表4.36。
表4.36 豇豆脱水正交试验因素水平编码表
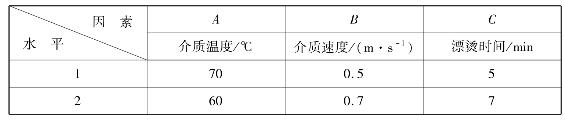
试验中,除考察因素A,B,C的单独作用外,还要考察任两个因素的交互作用。因此,试验选用L8(27)正交表。试验结果和极差分析见表4.37。
表4.37 豇豆脱水正交试验结果和极差分析表

2)多指标试验数据的极差分析
(1)综合平衡法
指标要有主次,对每一指标都作单指标极差分析。若某因素水平对绝大部分指标均优(要考虑指标的主次),则该因素水平为优。
(2)加权综合评分法原理:用y∗i=w1 yi1+w2 yi2+…计算综合指标,再按单指标进行极差分析。wj为各指标的加权系数。其步骤如下:
①定各指标的加权值wj,wj=1(根据各指标的重要程度而定)。
②消除各指标的量纲,使试验值处在同一数量级上。
计算各指标观测值的评分值y′ij:
设y′jmax=100分,yjmin=0分,则
![]()
③计算加权综合评分值为
![]()
注意:对越小越好的指标前为“-”号,综合指标越大越好。
④以y∗i为指标值再按单指标进行极差分析。
4.4.3 正交试验设计结果的方差分析法
极差分析的缺陷:一是不能解决因素对指标影响的显著性问题;二是若较优参数组合不是试验点,则其较优值无法知道。因此,要进行方差分析。
1)正交试验数据的分析
(1)数据结构
①数学模型为
yi=μi+εi
②μi分解为
μi+μ+各因素效应+各因素间的交互效应
真值为
![]()
因素效应:设μAm为A取第m水平的真值,am为其效应,则
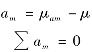
交互效应:设μAmBl为A取m水平、B取l水平的真值,(ab)ml为其效应,由双因素的数据结构可知
μij=μ+αi+βj+(αβ)ij
则
(ab)ml=μAmBl-μ-am-bl m
(ab)ml=l(ab)ml=0
引入估计值为
![]()
(2)计算工程平均值
即利用效应定量地估计各主要因素不同水平组合下可期望达到的指标值。
设
![]()
若较优参数组合为A2 B1 C2,则
![]()
式中,y^优为较优参数组合的预测值。
2)正交试验数据的方差分析
(1)方差分析的内容
①判断哪些因素对指标的影响是显著的,哪些是不显著的。
②找出参数水平的较优组合。
③较优组合方案指标的预测。
(2)方差分析的步骤(挂豇豆脱水试验表)
①计算各类平方和
对La(bc)正交表有
![]()
总体平方和为
![]()
自由度为
![]()
各列平方和:计算各列同一水平的指标和Km,m=1~b,则
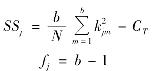
(对任一列,同一水平试验的次数看作是该水平下的重复)
误差平方和为
![]()
误差自由度为
![]()
注意:a.SS T=SSj,f T=fj。
b.当某交互作用同时占几列时,其平方和及自由度等于所占各列之和。
②因素及交互作用的显著性检验
计算均方差:因素及交互作用MS=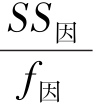 SS因 ,如
SS因 ,如
因
f因
![]()
误差为
![]()
F检验为
![]()
然后查F表,判断因素A的显著性水平。不显著的因素和交互作用应并入误差项重新进行显著性检验(注意:要逐项并入)。若并入一项后,原来显著的变得不显著,则不并入。
③选取较优组合
根据Km找出较优水平,根据F确定因素主次,确定交互作用的优搭配。
显著因素选较优水平,显著交互选较优搭配,若有矛盾且交互作用比单一因素显著,则以优搭配为主。
不显著因素若无显著的交互作用,则选合适水平,在以后的研究中作固定参数。
不显著交互作用忽略。
确定较优组合:显著因素选较优水平,不显著因素选合适水平。
④较优参数组合方案指标的预测
先根据数据结构算y^优(只考虑显著因素和交互作用),即
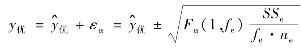
其中,n e=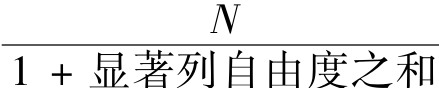 ,α为最低的显著性水平。
,α为最低的显著性水平。
例4.17 豇豆脱水试验的方差分析见表4.38。
表4.38 豇豆脱水正交试验结果和方差分析表
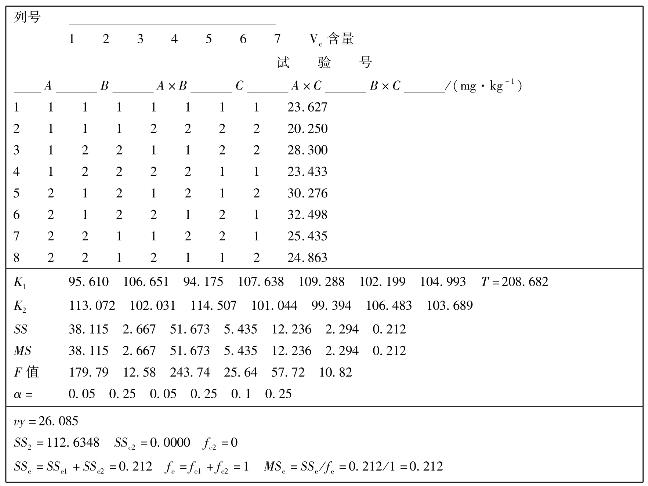
较优组合方案A2 B1 C2指标值的预测:
![]()
因各因素和交互作用均显著,故
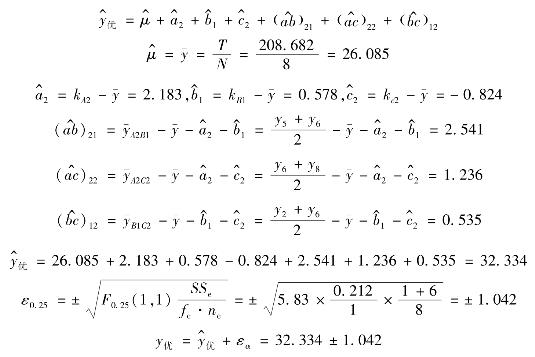
案例分析与讨论题
1.做一正交试验,研究A,B,C,D及A×B,B×C对指标的影响。各因素取2水平,指标越高越好。试安排正交试验并进行极差分析。
解 选正交表;
表头设计;
计算K1,K2,k1,k2,R;
选较优水平;
判断因素主次;
判断较优搭配;
判断较优组合。
正交试验结果和极差分析表见表4.39。
表4.39 正交试验结果和极差分析表

2.有一正交试验,其试验方案与结果见表4.40,指标越低越好。试进行极差分析。
表4.40
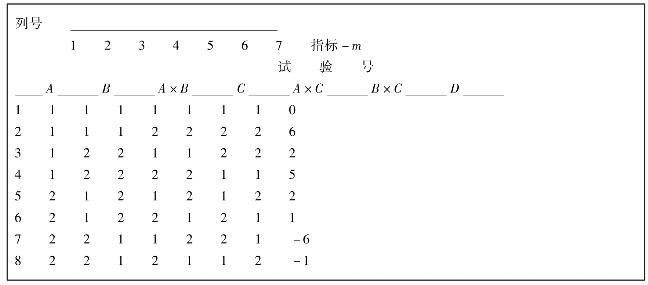
解 正交试验结果和极差分析表见表4.41。
表4.41 正交试验结果和极差分析表

3.做一正交试验,研究A,B,C,D及A×B,B×C对指标的影响。各因素取2水平,指标越高越好。试验方案和结果见下表,试进行方差分析并预测较优组合方案下的指标值。
解 计算T,C T,TT,SS T,ୱy;
计算SS,MS;
计算MS e;
计算F值;
进行显著性检验;
重算MS e;
重算F值;
重新进行显著性检验;
写出较优组合方案下指标预测的结构式;
计算y^优;
计算εα。
正交试验结果和方差分析表见表4.42。
表4.42 正交试验结果和方差分析表

vy=-0.500
SS2=146.000 0 SS e2=0.000 0 f e2=0
SS e=SS e1+SS e2=0.5 f e=f e1+f e2=1+0=1 MS e=SS e/f e=0.5/1=0.5
重算:将第6列、第7列并入误差列。
SS e=SS e1+SS e2=9.5 f e=f e1+f e2=3+0=3 MS e=SS e/f e=9.5/3=3.167
再算:将第1列并入误差列。
SS e=SS e1+SS e2=17.5 f e=f e1+f e2=4+0=4 MS e=SS e/f e=17.5/4=4.375
已知较优组合为A2 B1 C2 D2。
显著因素和交互作用有B1,C2,A2×B1。
因此,得
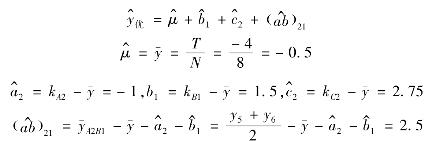
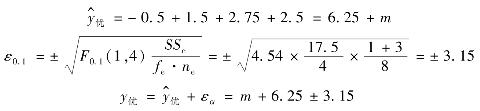
反思与练习
自溶酵母提取物是一种多用途食品配料,为探讨外加中性蛋白酶的方法,需做啤酒酵母的最适自溶条件试验,为此安排以下试验,试验指标为自溶液中蛋白质含量(%),取含量越高越好。因素水平表见表4.43。
表4.43
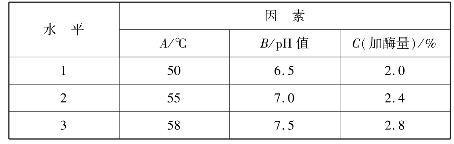
试验结果见表4.44,试进行直观分析和方差分析,找出使产量为最高的条件。
表4.44
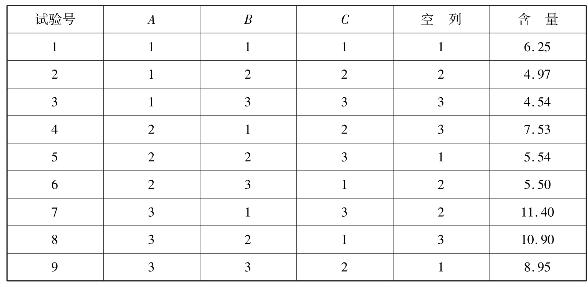
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
















