模型的非参数设定检验

如前所述，尽管关于ACD的实证研究已经十分丰富，却很少有人把注意力放在条件期间模型设定的测试上，我们利用国际上对金融高频数据研究的最新成果，在对中国证券市场高频数据建模进行实证研究的基础上，同时探讨关于ACD模型统计性质（如估计检验等）研究的最新成果。

这里我们研究采用两步法来测试条件期间模型的误差项的分布，第一步包括通过QML估计条件期间过程，以获得误差的一致估计；第二步衡量基准密度的参数和非参数估计与残差的风险率函数之间的紧密度。与Bartlett标识测试相比，两步法检测了残差的整个分布，而不是瞬间限制的一小部分。另外，这种测试没有多余参数，因为在用估计残差代替误差时没有渐近成本，而且，蒙特卡罗模拟表明这种测试对一些模型在有限样本和能量方面表现很出色。

表9.15　中国石化成交量期间消除日内效应ACD模型实证结果

注：① 成交量累积变动至少100万股。
② 括号内为标准差。
③D-test是对数残差的非参数检验概率值（p-values）。

（一）条件期间模型的简要介绍

假设xi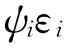＝，xi＝ti－ti－1表示在ti和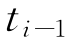时刻发生的两次事件的时间间隔，条件期望期间过程ψi＝E（ xi｜Ωi－1）为第i个期间持续的期望，｝～i.i.d，且与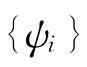相互独立，包括了时刻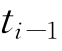时所有的有用信息集。我们可以用下列广义表达式将现有的ACD模型全部囊括进来：

式中，ui｜Ωi－1～N（ 0，），φ是一个参数向量。

例如：Engle和Russell（1998）的线性ACD（1，1）模型定义＝ω＋αx i－1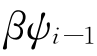＋。如果要模拟微观结构效应，也可以合并另外预先确定的变量（Engle and Russell，1998；Bauwens and Giot，2000）。

假设标准期间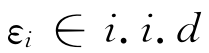具有Burr密度：

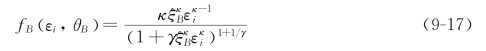
κ＞γ＞0，并且：

很容易看出xi的条件密度也是具有参数向量的Burr密度分布。相应地，条件风险率函数（conditional hazard rate function）为：

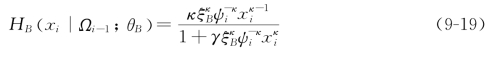
对于κ＞1时的标准期间是单调的。

γ→0时，（9-17）式可以简化为Weibull密度分布，即：

相应地，期间过程的条件分布也是Weibull密度分布，条件风险率函数为。与Burr分布相比，Weibull分布表示的条件风险率函数是单调的。在0＜κ＜1的标准区间里，它是递减的；当κ＞1时，它是递增的；当κ＝1时它是不变的。在后一种情况下，Weibull分布与指数分布一致，期间过程的条件风险率函数简化为。

Lunde（1999）提出了广义Gamma ACD模型，这里，具有密度^[7]：

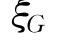≡。广义Gamma分布包含了标准Gamma分布（κ＝1）、指数分布（κ＝γ＝1）、Weibull分布（γ＝1），但没有包含Burr分布。因为基准风险率依靠不完全的Gamma积分，因此它没有解析解。然而，有可能根据参数值推导出它的形态特性，如果κγ＜1，当κ≤1时风险率函数递减，当κ＞1时风险率函数呈U型；相反地，如果κγ＞1，当κ≥1时风险率函数递增，当κ＜1时风险率函数呈倒U型。最后，如果κγ＝1，当κ＜1时风险率函数递减，当κ＝1时风险率函数不变（指数分布），当κ＞1时风险率函数递增。

尽管Engle和Russell（1998）建议使用指数和Weibull分布，Burr分布和广义Gamma ACD模型看起来对于价格和交易期间产生了更好的结果。如果准极大似然估计是建立在具有两个参数的标准Gamma分布基础上的，则准极大似然估计是一致的（Drost and Werker，2003）。

（二）模型设定检验

由于条件期间模型通常用（准）极大似然法来估计，因此似然比检验可用来比较条件期间模型中的不同分布。然而，由于参数空间的不等式约束，检验统计量的极限分布是χ2分布的组合，其概率权重信赖于参数估计的方差。因此，非常难以获得确切的渐近性实证的临界值。作为一种选择，Wolak（1991）建议应用渐近的边界检验，但是边界通常很松弛，很可能产生非决定性的结果。

下面设计一种检验方法，即通过匹配密度函数来检查标准区间分布的参数设定。更确切地说，就是假设条件均值过程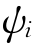被恰当设定，然后检验是否有任意一个参数向量值使得标准期间的参数密度函数和实际值几乎处于一致。首先需要考虑无效假设检验的一般问题：

与之相对应的备择假设则是：对于任意一个具有独立观察值x1，…，xn的非负随机变量X，都不存在这样一个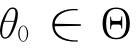。由于在非负随机变量X中起作用的标准持续区间是无法观察的，因此提出了本章第三节第四部分的改进内容，即检验条件期间模型的估计残差。

标准区间真实的累积分布函数F和密度f当然是未知的，另外，我们仅仅能够证实它们是否属于分布指定的参数家族，因此，我们不管分布参数的设定，使用Kernel方法来估计密度函数以获得一致的估计。因为参数密度估计值仅仅在无效假设下是一致的，所以很自然地可以考虑采用衡量这两个密度估计之间紧密程度的检验。

第一个检验程序，即标记的D-检验，依赖于衡量下述的距离：

∫x表示对x密度函数的积分是指标函数。根据由密度函数衡量的结果，（9-23）式表明了参数的和非参数的估计值之间的差异。此外，当且仅当x∈S，f（x）与f（x，θ）一致时，它是具有相等的非负数。我们引入子集S，以避免密度估计不稳定的区域。（9-24）式与（9-23）式相似：

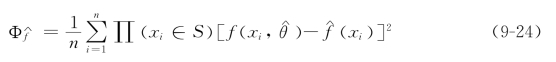
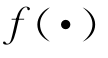分别表示真实参数θ0和真实密度的点态一致估计。如果D-检验统计量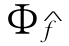足够大，无效假设将被拒绝。还可以用其他紧密度测量方法，如同在Fan（1994）里使用的对平方差积分而不是对均值积分^[8]。

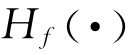由于连接风险率和密度函数的一对一映射的优点，无效假设（9-23）式表明：存在一个，使参数模型的风险率函数等于真实的风险函数。所以，我们认为第二个测试，即我们所说的H-检验信赖于统计量。

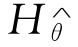和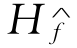分别是基准风险率函数的参数和非参数估计值。从以上讨论可知，（9-25）式在无效假设时接近0，在备择假设时比较大。

D-检验和H-检验统计量的极限分布不依赖于人们如何估计参数密度函数。这是从非参数密度估计收敛的速度比参数密度估计更慢的事实推导出来的，因此，可以采用极大似然方法。或者为D-检验和H-检验提供一个最小距离，通过最小化（9-23）式和（9-25）式来分别估计参数密度，由此产生的估计值和属于Newey（1994）讨论的M估计值的类别，因为其以两步骤程序来进行：第一步包含一个Kernel估计，第二步解决最小化的问题。

（三）实证数值结果

在此我们做了有限的蒙特卡罗试验以估计在有限样本时D-检验、H-检验的性能，因为在有限样本里大多数非参数检验都要承担实质性的尺寸失真（size distortions）的事实，例如，Fan和Linton（2003）证明了如何忽略容易产生这样的失真的更高阶项。尺寸失真是必然的，以至于要考虑D-检验和H-检验的引导基准（bootstrap-based）类型。正如Horowitz和Savin（2000）指出的，步步为营法（bootstrapping）允许有意义的尺寸校正临界值的计算，把效能数字放入预测之中，结果表明运用标准引导过程于估计残差效果很好，消除了尺寸失真的同时没有损害测试的效果。

通过描绘指数、Weibull（k＝0.6）、Burr（k＝0.5，γ＝3）以及广义Gamma（k＝0.5，γ＝3）四个分布的误差项，我们产生了线性ACD模型的15000个值，即：

设置α＝0.1，β＝0.7以匹配实证研究中发现的典型估计，而且，通过使ω＝1－（α＋β）来规范无条件期望期间为1，并且设上式中，连同全部样本（n＝15 000）一起，也考虑由最后3 000个值形成的子样本，以便减轻初始效应，这些是交易和价格期间数据的典型的样本尺寸，所有的结果都基于1 000个蒙特卡罗重复。

对每一个重复和数据产生过程，首先用指数分布计算QML估计值，最优化过程利用Han（1977）的连续二次程序运算法则，以便满足广义不等式约束，接下来，检查5个测试的结果：将Ghosh和Huang（1991）的最佳一致核心密度和Chen（2000）的Gamma核心密度运用到残差的D-检验和H-检验，并将最佳一致核心密度运用到对数残差的D-检验，用Silverman（1986）的拇指规则（rule-of-thumb）选择带宽，正态分布仅仅作为对数标准化期间的参考，其他的用指数做参考，这里也用log n来除拇指规则的带宽，例如，对于Gamma核心的带宽是：

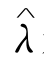是指数参数λ的一致估计，举例来说，就是样本均值的反转。

为了评价6个测试的尺寸和效果，计算了无效假设的拒绝频率，通过将估计模型套入真实模型的所有例子来更精确地调查尺寸失真，比如，尽管真实分布是指数分布，但可能性考虑的却是一个Burr密度，相反，为了调查这些测试的效果，检测估计模型不包含真实设定的情况，比如，估计模型设定指数分布，然而真实密度却是一个Burr密度。

渐近检验建立在最佳一致核心密度真实尺寸失真的基础上，除非是运用有些自由无关的数据生成过程的对数残差，步步为营地估计残差足以校正测试的尺寸而不影响它们的效能，相反，渐近Gamma基础的检验在尺寸和效能方面执行起来相对要好，因此没有必要采用步步为营的方法。我们发现，检验结果表现出很好的效果，除非想要把广义Gamma分布和Burr分布之间区分开来，具有最佳核心密度的H-测试有最差的表现：当真实的基准分布是广义Gamma时，它几乎从不拒绝Burr ACD设定。

为了比较，我们也对具有指数和Weibull分布的ACD模型进行Engle和Russell（1998）提出的过度分散检验，过度分散检验的效果令人失望，而具有Gamma核心密度的D-测试和H-测试似乎具有最好的表现。然而对于对数标准期间D-测试是一个更好的选择，因此我们随后仅用D-检验实际检验第四部分建立的模型。

（四）D-检验实证结果分析

D-检验就是通过衡量残差密度函数的参数和非参数估计值之间的紧密程度，来检验模型设定的优劣。在ACD模型正确设定的条件下，残差的参数估计值和核心密度估计值都趋向真实的Burr密度分布，相反，错误设定的模型则会由于因子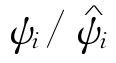在概率上不趋向于1从而提高Burr分布的混合值，核心密度估计值会趋向于Burr密度的混合值，而参数估计值总是属于Burr家族的，测试统计值在无效假设下有可能趋于0，然而在备择假设下它可能会比较大。运用D-检验有许多有利之处：第一，D-检验测试较为简单，易于操作；第二，与Bartlett标识测试相比，D-检验检测了残差的整个分布，而不是其中的一小部分；第三，D-检验没有多余参数，因为在用估计残差代替误差时没有渐近成本，而且，蒙特卡罗模拟表明这种测试对一些模型在有限样本和能量方面表现很出色；第四，D-检验对固定的和局部的改变具有很好的统计效能。

为了避免核心密度估计值的边界效应，我们用对数残差而不是普通残差，所有的非参数密度估计值用Gaussian核心密度分布，然而带宽根据Silverman（1986）的拇指规则来选择，进行这种修正是必要的，因为D-检验的渐近理论要求一个低平滑度以避免附带的偏差项。

下面，我们运用D-检验对第四部分的模型进行实证研究，数据结果列示于表9.12至表9.15的D-test列。D-检验值较好的模型，其非参数密度估计值很好地围绕对数残差的参数密度估计值波动，反之则不然。

对比对数似然值可以发现，一般对数似然值较低的模型其D-检验值则较大，然而，对数似然值在不同的模型中，有时差异较小，而D-test值差异较大，说明D-检验方法的灵敏度更好，因此两种检验方法具有一定的互补性。

综合考虑所有的实证结果，通过AIC以及D-检验值的对比，BC-ACD、EX-ACD以及L-ACDⅡ三类模型实证结果的成功率最高（即模拟效果较好的次数相对较多），因此，我们认为这三类模型产生了最好的效果。