(一)有效边界的概念
在现实生活中,人们投资的目的因人而异,各不相同,然而作为一个理性的投资者,他的投资动机是为了获取利益,因为收益可以给投资者带来某种满足,或者说带来一定的效用。一方面,收益越大,投资者从中得到的满足越多,从而效用越大,因而理智的投资者总是力图增加收益;但另一方面,风险也相伴而生,而风险是对效用的一种损害,因此投资者总是力图减少风险。所以投资者必须在收益和风险之间做出权衡,使其效用达到最大。这样投资者必然采取以下策略:第一,在风险相同的条件下,选择期望收益最大的证券品种;第二,在期望收益相同的条件下,选择风险最小的证券品种。
在此基础上,为了便于分析,马柯维茨提出如下假设:(1)市场是有效的,即市场上的任意证券信息都是已知或可以知道的;(2)投资者是风险的厌恶者;(3)所有投资决策都是依据投资的期望收益及其方差做出的;(4)投资单元是完全可分的,即假定所有的证券是无限可分割的,投资者可按任意比例买卖;(5)收益率和风险是并存的,要想得到高收益,就必须承担高风险。
马柯维茨根据他的假定和西方经济学的效用理论分析指出:投资者的行为将是一个寻找有效组合的过程。所谓有效组合,是指该证券组合与其他证券组合相比,在同样的风险水平下,具有最高的收益率;或者在同样的收益水平下,具有最小的风险,而有效边界就是由所有的有效组合在风险—收益平面上所形成的曲线。
举例来说,对表7.6所示的选择对象,根据马柯维茨理论,投资者对于证券组合D的偏好胜过对证券组合B的偏好,因为两者具有相同的8%的预期收益,但是证券组合D的4%的风险比证券组合B的12%的风险要小。同样根据马柯维茨理论,投资者对于证券组合G的偏好将胜过对证券组合F的偏好,因为这两种证券组合具有相同的11%的风险,但是证券组合G的10%的预期收益比证券组合F的6%的预期收益要高。同样的道理,投资者对于证券组合A的偏好将胜过对证券组合C的偏好。
表7.6 若干可供选择的证券组合


图7.13 有效边界
在证券投资学中,把上述分析概括成一个定理:一个投资者将从在各种风险水平能够带来最大收益率的,以及在各种预期收益率水平上风险最小的证券组合边界中选择出最佳证券组合。这条定理称为有效边界定理。满足这个定理的证券组合边界叫做有效边界。图7.13画出了表7.6列示的7种证券组合的预期收益和风险的搭配情况,曲线ADG代表有效边界,它由满足有效边界定理的证券组合连接而成。
(二)有效边界的确定
1.图解法
图解法可以清楚、直观地表现有效边界,这不能不说是一大优点。但是,用图解法求解有效边界又相当麻烦,所以这种方法仅适用于证券种类不超过三种的投资组合。下面以三种证券投资组合为例,说明有效边界的确定。
【例7-3】 假设三种证券A、B、C,它们的投资收益分别为RA、RB、RC,风险分别为σA、σB、σC,在证券组合中所占的比例分别为XA、XB、XC,协方差分别为σAB、σBC、σAC。由于XA+XB+XC=1,则XC=1-XA-XB,则该证券组合的预期收益为:
![]()
可以求得XB关于XA的函数:

(7-16)式表示在 已知的情形下,XA与XB的组合关系,其斜率为
已知的情形下,XA与XB的组合关系,其斜率为![]() 与纵轴的交点为
与纵轴的交点为![]() 由此可知,若
由此可知,若 改变,斜率不会受影响。因此,可以根据不同的
改变,斜率不会受影响。因此,可以根据不同的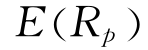 的值,在XA、XB坐标上画出等收益直线。等收益直线的意义就是表示在该直线上的每一点均有相等的收益率,在相同收益条件下证券组合的不同比例。
的值,在XA、XB坐标上画出等收益直线。等收益直线的意义就是表示在该直线上的每一点均有相等的收益率,在相同收益条件下证券组合的不同比例。
上述三种股票的收益率、方差、协方差等数据如表7.7所示。
表7.7 三种股票的收益率、方差、协方差数据

根据表7.7中的数据,可以计算出斜率为:

截距为:

这样,其截距的值取决于所希望的证券组合的预期收益率。假设我们想找到给我们带来10%的预期收益率的那些证券组合比例的边界。在这个例子中,其截距为:
![]()
则10%的预期收益率直线的公式为:
![]()
假设投资者对股票A的投资用去资金的50%,即X A=50%,根据上述公式,则必须对股票B不予投资,而将余下的50%的资金投资于股票C,以组成一个预期收益率为10%的证券组合:

当然,不仅仅这样的比例可产生10%的预期收益率。例如,将XA=1.00,XB=-1.00,XC=1.00组合也可以得到相同的效果。考虑三种股票各种投资比例的组合,这些组合均使用证券组合的预期收益率为10%。这些组合在图7.14中以标有10%的等预期收益率直线表示。
图7.14 等收益直线
如果投资者想看到对应于有价证券组合预期收益率不同数值的那些投资比例的组合,那么就必须研究不同的等预期收益直线。例如,图7.14中标有12%的直线表示的比例组合对应的就是那些能够产生12%预期收益率的证券组合。
在上面这个例子中,如果曲线向右上方移动,则移向预期收益率越来越低的等预期收益率直线。这些等预期收益率线都具有负的斜率。一般来说,斜率和等预期收益率线的相对位置取决于所考虑的三种股票的相对的预期收益率。为了说明这一点,假设投资者换掉股票A和股票C的预期收益率。在这种情况下,虽然直线仍具有负的斜率,但当曲线向右上方移动时,则表示投资者移往预期收益率越来越高的等预期收益率直线。
下面阐述在相同标准差条件下的不同投资比的证券组合。将XC=1-XA-XB代入求方差的公式可得:
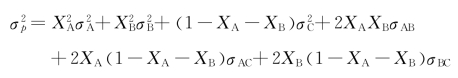
可得:

(7-17)式为一个二元二次方程式,其一般形式为:
![]()
投资者可以了解其如椭圆的通式,并可以画出方差相同的椭圆曲线,如图7.15所示。在椭圆上的任一点表示有相同的方差。如同存在等收益直线族一样,也存在一族等方差椭圆,每一个椭圆代表收益率方差为某一水平的证券组合的边界。

图7.15 等方差椭圆曲线
【例7-4】 接上例,假设投资者想找到对应于有价证券组合方差为30%的证券组合投资比例椭圆。为了确定椭圆的两点,对XA任取一值,比如这里取XA=0.00,并且把这个值用表7.7中的方差和协方差代入方差公式:


经简化后得:
0.30=0.28-0.38XB+0.31
这是一个二次方程,所以XB有两个根,XB的两个值为:
 =1.28,
=1.28, =-0.05
=-0.05
从而,方差为30%的两个证券组合为:
XA=0.00,XB=1.28,XC=-0.28
或
XA=0.00,XB=-0.05,XC=1.05
这两个证券组合在图7.16中以点W和点X标出。这只是方差为30%的等方差椭圆上许多证券组合中的两个证券组合。为了找出两个点,我们再对XA任取一值,比如XA=1.00,把XA这个新值代入证券组合方差方程,并再次求解,得到XB的两个根,它们在图7.16中以点C和点B表示。通过反复重复这个计算过程,可以得到所希望得到的椭圆上的许多点。但是,若对于XA的任选值,XB无解,这就意味着若股票的特性已定,不论XA取何值,要构造一个方差低至30%的证券组合是不可能的。因此,XA所取的值必须在方差30%的椭圆水平范围之外。
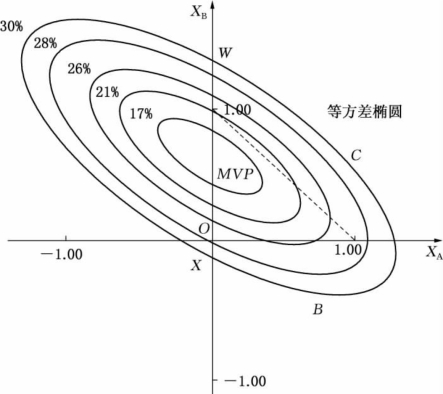
图7.16 等方差椭圆
投资者若想画出与另一个 值相对应的椭圆,只需另选一个所需要的方差值,将它代入证券组合方差方程,然后按上述步骤进行计算。如果所选的证券组合收益率方差低于30%,投资者将会发现新的椭圆在原来方差为30%所对应椭圆的内部。随着所选的证券组合的方差变小,椭圆也变得越来越小,最后收敛于MVP点。对于给定的含有三种股票的协方差矩阵,MVP则表示了可能达到的最低的证券组合方差。如果投资者想再找到一个证券组合方差更小的椭圆,就会发现无论X A取何值,方程都无解。这里需要指出,所有椭圆均同心于MVP点。
值相对应的椭圆,只需另选一个所需要的方差值,将它代入证券组合方差方程,然后按上述步骤进行计算。如果所选的证券组合收益率方差低于30%,投资者将会发现新的椭圆在原来方差为30%所对应椭圆的内部。随着所选的证券组合的方差变小,椭圆也变得越来越小,最后收敛于MVP点。对于给定的含有三种股票的协方差矩阵,MVP则表示了可能达到的最低的证券组合方差。如果投资者想再找到一个证券组合方差更小的椭圆,就会发现无论X A取何值,方程都无解。这里需要指出,所有椭圆均同心于MVP点。
等预期收益率线与等方差椭圆重叠画于图7.17中。直线NY为临界线,它表示出最小方差边界中的证券组合的投资比例。通过描述等预期收益率线与等方差椭圆相切的点的轨迹就可以得到临界线。可以说,如果找到了最小方差边界,就找到了临界线的位置。
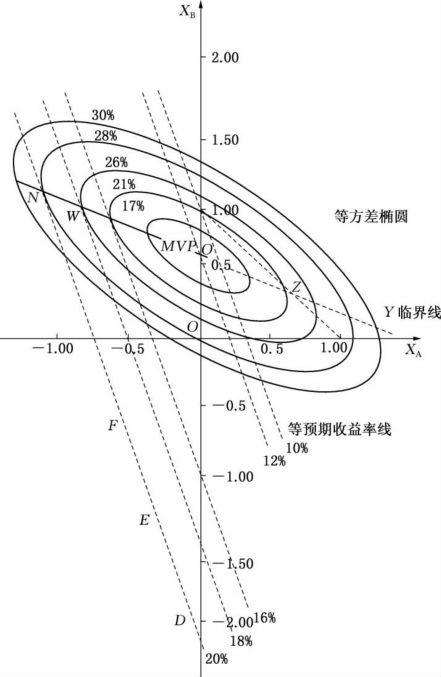
图7.17 最小方差边界中证券组合的投资比例
在图7.17中,N点的证券组合的方差为28%,点N也是28%等方差椭圆与20%等预期收益率线相切的切点。这就是说,找到预期收益率20%的最小方差为28%,其证券组合的投资比例近似为:XA=-1.00,XB=1.00,XC=1.00。其他证券组合最小方差边界的点都在图7.17中一一找出。
根据临界直线不同的XA、XB的组合,可以计算出临界直线反映的σp和E(Rp)的值,在E(Rp)、σp的坐标系上,可以获得有效边界,如图7.18所示。

图7.18 股票A、B、C的有效边界
2.数学分析法
由于图解法在求解有效边界中有一定的困难,因此,在马柯维茨证券组合理论中引入了一些数学分析方法,这些方法对于从事从有效边界到最佳投资组合选择的推导,起到了良好的效果。
(1)极小微分法。
当证券组合中包含三种以上的证券时,图解法就不能用了,但是投资者可以利用极小微分法。
三种以上的证券组合方差为:

根据有效边界定理,投资者在收益率一定的条件下,总是寻求风险最小的证券组合,也就是要在给定的条件下,求出极小的σp。根据证券组合预期收益率公式,以及证券组合中各种不同投资比例可以得到以下方程组:

式中,(2)式和(3)式两式为(1)式的限制函数,利用拉格朗日目标函数,引入λ1和λ2,可得如下方程:
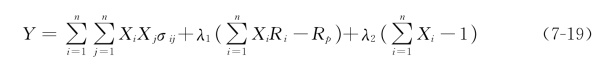
为了使风险最小,则将(7-19)式对所有的Xi以及λ1和λ2作偏微分,并使微分方程为0,所以得如下方程组:
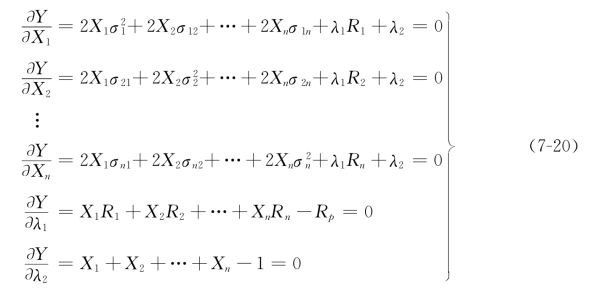
(7-20)方程组由(n+2)个一次方程式组成,含有X1,X2,…,Xn,λ1,λ2共(n+2)个未知数,解此联立方程组,结果可使Xi具有如下形式:
![]()
式中,i=1,2,…,n;ai、bi为常数。
给出不同的Rp,则可以得到不同的Xi,并求出σp,这样就可以得到有效边界曲线。
投资者也可将(7-20)方程组转换成矩阵等式的形式:

其中,系数矩阵用K表示,变数向量用X表示,C为常数向量,则上述矩阵形式可写为:
KX=C
利用K的逆矩阵形式,可得:
![]()
结果也会是(7-21)式的情形。如果利用计算机,可以迅速求出Xi的值,然后求Rp和σp,可以得到有效边界。
【例7-5】 下面举例说明在三种证券组合时,用极小微分法的求解过程。假设有关资料如表7.8所示。
表7.8 三种证券的预期收益率、方差和协方差

三种证券组合时,取得方差最小的各组Xi之值可由下列矩阵方程求出。

将表7.8中数据代入上式得:
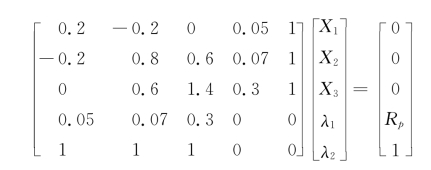
运用初等变换得到系数矩阵为:

在矩阵方程两边同时左乘C矩阵得到:

取Rp等于一系列符合统计意义的数值时,根据:

就能求出对应的各组Xi值,也就求出了在收益率一定的条件下方差最小的证券组合,即有效证券组合。根据各组X 1、X 2和X 3的值求出对应的各组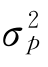 及E( R)的值,就可以在E( R)、
及E( R)的值,就可以在E( R)、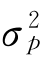 坐标系中绘出有效边界了。
坐标系中绘出有效边界了。
下面利用上海证券市场的实际资料对这一问题做实证分析。为了使实证分析更科学,对于公司股票在分散公司所属行业的前提下,应尽量选取有一定上市时间的股票。经筛选,所选择的15种股票所属的行业及上市日期如下:工业类6种,它们是:真空电子(1990年12月上市)、联合实业(1992年3月上市)、异型钢管(1992年3月上市)、嘉宝实业(1992年11月上市)、飞乐股份(1990年12月上市)、凤凰化工(1990年12月上市);商业类2种,它们是:飞乐音响(1990年12月上市)、豫园商城(1992年8月上市);房地产类2种,它们是:兴业房产(1992年1月上市)、浦东金桥(1993年3月上市);公用事业类2种,它们是:大众出租(1992年8月上市)、国脉实业(1993年4月上市);综合类3种,它们是:延中实业(1990年12月上市)、爱使电子(1990年12月上市)、申华实业(1990年12月上市)。
在分析证券时,考虑到1992年5月21日以前,上海证券交易所对每日建议的涨跌幅有所限制,故分析的时间取为1992年6月至1994年6月。
这里,对收益率的计算采用周收益率为衡量标志,其计算方法为:
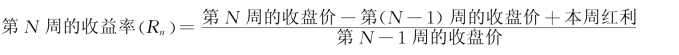
若在本周内发生送配股现象,则在计算本周收益率时,先将第N-1周的收盘价折算成相当于送配股后的价格,再代入上述公式,折算方法为:

现给出计算结果。兹以组合预期收益率(Rp)分别为0%、0.2%、0.5%、0.8%、1.0%、1.2%、1.5%、2.0%和2.5%为例,计算得各自的最小风险及各证券的投资比例,如表7.9所示。
表7.9 允许卖空时的有效组合
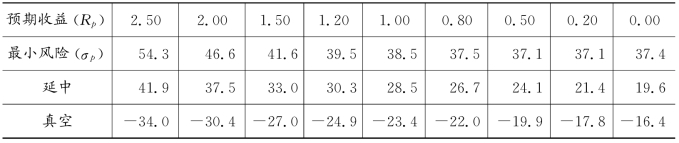
续 表
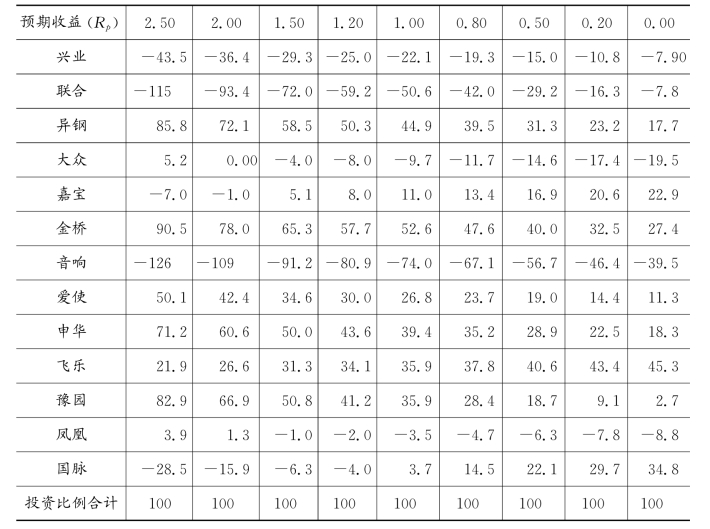
注:表中预期收益为周收益率,风险为方差值,权数为百分比,以后各表同此。
表7.9数据中,负数表示卖空操作。以预期收益为2.5为例,此时延中股票的权数为41.9,真空股票的权数为-34.0,这意味着若投资者有100元的资金可用于投资,则对延中股票,在期初应买入41.90元,到期末再抛出;对真空股票,假定其期初价格为3.40元/股,则在期初应从经纪人手中借入10股,并将之卖出,所获得的34.00元可用于投资其他证券,到期末再购买10股真空股票归还经纪人。投资者根据计算所得的比例,对各股票分别采用卖空手段或正常的先买后卖的方法,可望获得周收益率为2.5%的报酬。
由表7.9可以看出,计算结果呈现出较强的规律性:当期望收益降低时,正常买入的股票权重下降,同时卖空股票的比重也下降,如果要得到较高的收益,则对一些收益率较低的股票要大量采用卖空手段,对收益高的股票则要大量买入。另外,预期收益率下降时,最大风险也相应地下降,但下降的速度逐渐变慢,当预期收益下降到一定程度(如0.00)时,风险不仅不能减小,反而增大了。这是因为通过求解方程得到的解是局部极小值。有效边界的形状在方差—收益平面上,是一开口朝右的抛物线的上半支。当收益下降到一定程度时,通过方程求解得到的解已是这条抛物线的下半支部分,因此这些点已不属于有效边界范围。在这种情况下,正确的方法应是在此最小风险条件下,求最大收益率,从表7.9中可估计出这个周收益率大致在0.6%左右。

图7.19 允许卖空时15种股票的有效边界
15种股票的有效边界可用图7.19表示。
(2)极大微分法。
同极小微分法一样,极大微分法是计算投资组合中收益率为最大的情形,进而求出有效边界曲线。
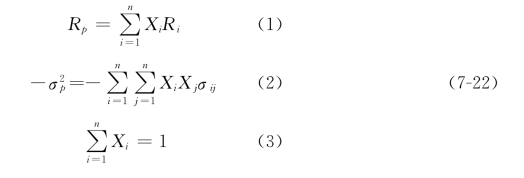
(7-22)式中的(3)式是限制函数,要求出 的极大值。同时假设Φ为投资者的风险规避系数,Φ值从0到无穷大。若Φ=0,表示投资者是风险喜好者,愿意承担相当大的风险;若Φ→∞,则表示投资者较为保守,不愿意承担太大的风险。在极大微分法中,须在Rp前乘Φ。所以,利用拉格朗日目标函数法,由(7-22)方程组得到如下函数形式:
的极大值。同时假设Φ为投资者的风险规避系数,Φ值从0到无穷大。若Φ=0,表示投资者是风险喜好者,愿意承担相当大的风险;若Φ→∞,则表示投资者较为保守,不愿意承担太大的风险。在极大微分法中,须在Rp前乘Φ。所以,利用拉格朗日目标函数法,由(7-22)方程组得到如下函数形式:
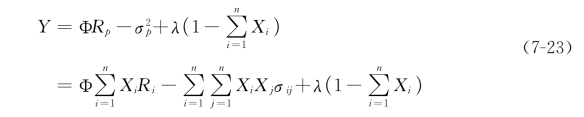
要求Y值的极大化,将Y对所有的X i以及λ求偏微分,并使其为0,可以得到下列(n+1)个一次线性方程组:
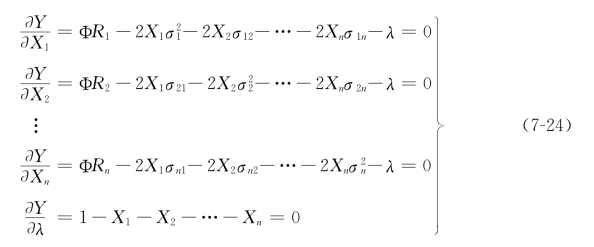
Φ为常数,则(7-24)方程组中一共有(n+1)个方程式和(n+1)个未知数,如此可以解出:
![]()
式中ai和bi为常数,将不同类型投资者的不同数值的Φ代入,即求得Xi,进而求得Rp和σp,在坐标系上可以得到不同的证券组合,并画出有效边界曲线。
与极小微分法相类似,也可将(7-24)方程组转换成矩阵形式,利用逆矩阵来求得有效边界曲线上的证券组合。

(3)二次规划法。
用微分法来求出有效边界曲线,较图解法要方便得多。但是,如果对投资比Xi的范围有所限制时,例如Xi不可以为负值,即Xi≥0时,微分法就不能使用了,而需要通过二次规划法来处理。
在我国,目前卖空是不允许的,即Xi不能为负值,而且现实中任意贷款也是不可能的。另外,由于法规的限制及一些人为的因素,投资者往往也要对投资某种证券的比例做出限制,因此,研究这种情况具有很现实的意义。
然而,这种情况在数学处理上比前两种情况要复杂得多,其原因是约束条件引入了不等式。其数学模型为:
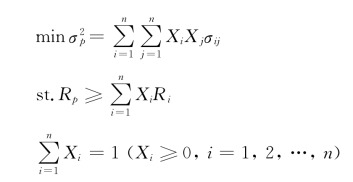
这是一个含有不等式的二次规划问题。用二次规划法确定最优证券组合是马柯维茨提出来的。解决二次规划问题,数学上有不少方法,这里介绍常用的有效集法。其基本思想是选取一个初始的可行解,找出该点的有效集,然后按照使其目标函数值下降的原则,对有效集不断调整,最终使目标函数达到最小。
为了便于拓展,假定有如下标准的二次规划问题:

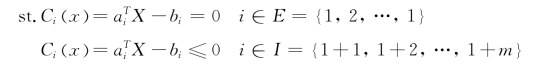
其中,G为N×N阶正定矩阵,X为N维向量。
定义:设X 0是上述问题的可行点,若某个j使得Cj(x)=0,则称约束Cj(x)=0或Cj(x)≤0为X 0处的有效约束,称所有X0处有效约束的指标组成的集合:
![]()
为X 0处的有效集。从而上述问题可用如下算法求得最优
第一步:取初始可行解X(1),确定相应的有效集A(1线性无关,置K=1。
第二步:求解仅含等式约束的严格凸二次规则:
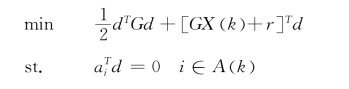
其中,d为N维向量。即求解线性方程:
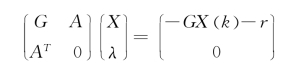
记方程组的解为d(k)。
第三步:若d(k)=0,则计算相应的拉格朗日乘数 [i∈A(k)],否则转至第五步。
[i∈A(k)],否则转至第五步。
第四步:若对任意i∈A(k)∩I,都有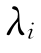 ≥0,则X(k)为原问题的解,停止计算。否则求出:
≥0,则X(k)为原问题的解,停止计算。否则求出:
![]()
置X(k+1)=X(k),置A(k+1)为X(k+1)处的有效集,然后转至第二步。
第五步:若X(k)=X(k)+d(k)满足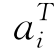 X(k)-
X(k)-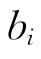 ≤0[i∈l∩A(k)],则置X(k+1)=X(k),置A(k+1)为X(k+1)处的有效集,然后转第二步。
≤0[i∈l∩A(k)],则置X(k+1)=X(k),置A(k+1)为X(k+1)处的有效集,然后转第二步。
第六步:计算
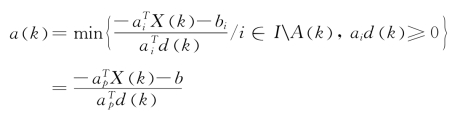
并置X(k+1)=X(k)+a(k) d(k),A(k+1)=A(k)+{P},然后转至第四步。
根据上述算法,对上述实证分析中所举上海证券市场15种股票组合的实证分析数据计算如表7.10所示。
表7.10 不允许卖空时的有效组合

表7.10中数据说明:不允许卖空时,如要得到高收益,则投资者必须将资金投到少数几种高收益的股票上去,如音响、爱使、金桥等。当对收益的要求降低时,投资到音响上的股票资金将迅速减少,这是由于音响股票与其他的入选股票相关程度很高,风险较大。当预期收益下降到一定程度时,国脉股票也可进入组合,因为它与其他股票的相关性很小,引入组合可以减小风险。表7.10中15种股票的有效边界的形状见图7.20。

图7.20 不允许卖空时的有效边界
由上述分析可知,用微分法求解有效组合时,只需解一个线性方程即可,因此能简洁地处理组合中含有多种证券的情况,这使得它成为证券投资分析者最常使用的方法。但其缺点是无法处理对投资比例有所限制的情形。而二次规划法则具有广泛的适用性,可以解决在各种限制条件下的有效组合问题。使用这种方法一般要多次迭代,因此只能在计算机上实现。这种方法对一般的投资基金或投资机构而言,具有很大的应用价值。
(4)线性规划法。
我们知道,如将风险看作实际收益率与预期收益的偏差,则方差或标准差并不是天然的风险度量器具,真正的风险应该是所有的偏差之和。之所以不采用方差作为风险的度量,主要是由于绝对值函数不是一个连续可导函数,为了便于数学上的处理而采用平方法将离差非负化。然而,就证券组合这一特定问题而言,使用绝对偏差作为风险度量在应用上是可能的。为此,日本学者Hiroshi Konno在1990年的《日本运筹学学会学刊》上提出了一种令人耳目一新的方法。他将求解有效组合问题化为一个线性规划问题,使求解证券组合大为简化。其基本过程如下:
首先,利用绝对离差作为风险的衡量。则求有效组合的模型为:

Kj表示对证券j的比例限制。
若Rjt为证券j在时期t(t=1,2,…,T)的收益观察值,以Rjt的平均值作为期望收益的估计,即:
![]()
则

为了消除目标函数中的绝对值,我们采用一种变形处理。因为最小值问题:

与下列线性规划问题等价:

即F取得最小值时,Z(x)也同时取得最小值。于是原始问题可化为:


上述问题的目标函数及约束条件都是线性的,这样将解决证券组合问题转化为解一个线性规划问题。由于线性规划问题在数学上已有较完备的理论,解决的通用软件多,因此模型应用十分方便。且加入参数或改变参数值后,修改模型也可很快实现,因为线性规划中灵敏度分析理论已成功地解决了这些问题。运用灵敏度分析,改变某一证券的预期收益率,可快速测算证券组合的变化,也可通过改变预期收益率,求出在绝对离差作为风险时的证券组合的有效边界。
这个模型在日本的一些投资公司已得到应用,根据日本野村证券公司测算,以此模型为基础,运用线性规划软件求解225种股票的组合投资,平均费时仅3.3分钟,比原来各种模型均快90%以上,且预测效果不亚于原有模型。
然而,这个模型的缺点是不便于进一步的分析处理,如分析证券之间的相关程度,以及进行显著性检验,确定置信区间等,因此它能否推广,有待今后的实践检验。
(三)有效边界的凹性
前面已经指出,风险回避型投资者的无差异曲线是凸性的。这里,我们将说明,有效边界一般是凹性的,即如果在有效边界上的两点画一条直线,这条直线将位于有效边界的下方,有效边界的这一特点说明投资者无差异曲线和有效边界曲线只有一个切点。
为了证明有效边界具有凹性,现考虑下列包括两个证券组合的例子。
证券1,估计预期收益率R1=5%,标准差σ1=20%;证券2,估计预期收益率R2=15%,标准差σ2=40%。我们考虑投资者购买这两种证券的所有可能组合。X1和X2分别代表各自的投资比例,X1+X2=1。表7.11列出了7种不同的投资方案。
表7.11 7种不同的投资方案
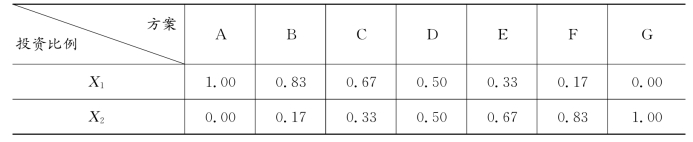
为了考察这7种可能投资的证券组合,必须计算它们的预期收益率和标准差。计算这些证券组合预期收益率的所有必要条件都已给出,利用下式可得:

代入X1和X2,证券组合A和G的收益率分别为RA=5%和RG=15%。证券组合B、C、D、E、F的预期收益率则可分别计算如下:
R B=0.83×5%+0.17×15%=6.70%
R C=0.67×5%+0.33×15%=8.30%
R D=0.50×5%+0.50×15%=10%
R E=0.33×5%+0.67×15%=11.70%
R F=0.17×5%+0.83×15%=13.30%
这些证券组合的标准差可以利用下式求得:
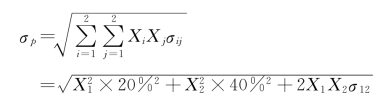
证券组合A和G计算简单,因为只包括一家公司股票,所以它们的标准差分别为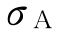 =20%和
=20%和 =40%。
=40%。
证券组合B、C、D、E、F的标准差取决于两个证券的协方差的大小,如前所述,两种证券的协方差等于它们的相关系数和各自标准差的乘积:

因此,这两种证券构成的任何证券组合的标准差都可以表示为:
![]()
比如,代入证券组合D的X1和X2值,它的标准差就成为:

当相关系数 取最小值-1时,
取最小值-1时,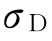 也最小。因此
也最小。因此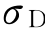 的下限为:
的下限为:
![]()
同样,当相关系数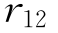 取最大值1时,
取最大值1时, 也最大。因此
也最大。因此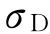 的上限为:
的上限为:
![]()
一般来说,对于任何给定的X1和X2两种证券的相关系数分别取最小值-1和最大值1,就可以求出证券组合标准差的下限和上限。表7.12列出了7种证券组合标准差的下限和上限。
表7.12 证券组合标准差的下限和上限
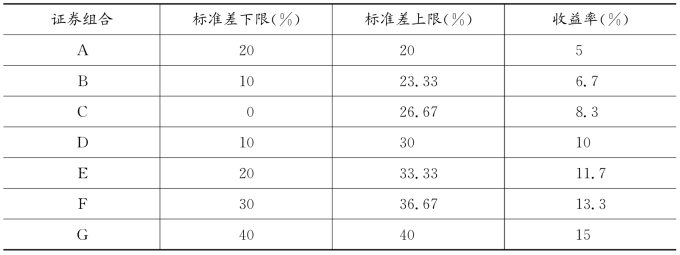
将表7.12中的这些数据描绘在图7.21上,就得到了证券组合风险分析的图形。

图7.21 证券组合风险分析
图7.21中A、G两点所连成的线段上的点分别表示收益率与标准差上限组成的点。所有的上限全部落在A点和G点连成的直线上。这就意味着,由这两种证券构成的任何证券组合的标准差都不会位于连接这两种证券的直线的右边。相反,它们只能位于这条直线上,或者位于它的左侧。这种现象说明了证券投资分散的意义。一般而言,分散投资能够降低风险程度,这是由于证券组合的标准差只能等于或小于证券组合中各个证券标准差的加权平均值。
相应地,图7.21中的B′、C′、D′、E′和F′则表示收益率与标准差下限组成的点。也就是说,这些证券组合的下限位于两条线段中的一条,即从A到垂直轴上的8.3%点处间的线段,或从垂直轴上8.3%点处到G点间的线段。包含有这两种证券的任何证券组合的标准差都不会出现在这两条线的左边。例如,证券组合B位于通过垂直轴上6.7%点处的水平线上,其下限和上限值分别为10%和23.33%。
由此可见,包含有这两种证券的任何证券组合的点都位于AC′G三角形内,至于证券组合点的确切位置则依赖于两种证券相关程度的大小。
如果相关系数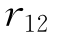 =0,则证券组合的标准差变成如下的形式:
=0,则证券组合的标准差变成如下的形式:
![]()
将不同方案的X1和X2代入,可得证券组合A、B、C、D、E、F和G的标准差如下:
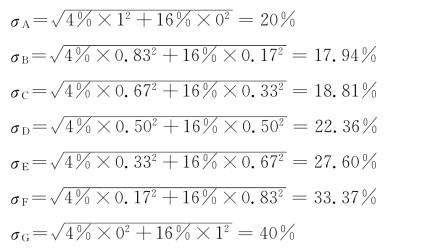
将这一组标准差与它们对应的收益率组合,可在图7.21上得到B0、C0、D0、E0和F0,将这些点用光滑的曲线连接起来,就可以得到一条凹性有效边界曲线。由此可见,有效边界曲线是位于三角形AC′G内的凹性曲线,其凹性程度依赖于两证券间相关系数的大小,相关系数越趋向于+1,曲线会变得直一些,越接近于AG线段;相关系数的值越小,曲线越弯,也越接近于三角形的另外两条线段。
从两种证券组合分析得到的结论,同样适用多种证券组合的情况。只要相关系数大于-1和小于+1,证券组合构成的形状就为凹性。因此,可以得出一般的结论,有效边界具有凹性。
(四)最优证券组合的选择
我们已由有效边界的含义知道,有效边界上的所有点对应的证券组合在收益一定的条件下风险最小,或者在风险一定的条件下收益最大,而有效边界以上的区域都是不可能的组合。因此,投资者所要选择的最优证券组合只能从无差异曲线及有效边界相切的点中求得。

图7.22 有效边界及无差异曲线切点图
现设 、
、 和
和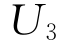 为3条无差异曲线,ABC为有效边界,如图7.22所示。
为3条无差异曲线,ABC为有效边界,如图7.22所示。
在图7.22中,尽管 的效用期望值最大,投资者可能偏好在这条无差异曲线
的效用期望值最大,投资者可能偏好在这条无差异曲线 上的点,但是它处于有效边界的上方,也就是说,它处于不可能证券组合的区域。因此,这只是投资者的一种愿望,而不是现实。对于无差异曲线
上的点,但是它处于有效边界的上方,也就是说,它处于不可能证券组合的区域。因此,这只是投资者的一种愿望,而不是现实。对于无差异曲线 来说,由于
来说,由于 <
<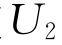 ,投资者总是偏好
,投资者总是偏好 上的点。
上的点。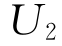 刚好与有效边界相切于B点,它比任意一条与有效边界相交的无差异曲线
刚好与有效边界相切于B点,它比任意一条与有效边界相交的无差异曲线 对应的效用期望值都大。因此,投资者选择B点上的证券组合为最优证券组合。
对应的效用期望值都大。因此,投资者选择B点上的证券组合为最优证券组合。
根据不同投资者对于投资效用的不同理解,对于高度风险偏好型和轻度风险偏好型的投资者来说,他们的最优证券组合如图7.23和图7.24中的 和
和 所示。如果假定最优证券组合的收益率和方差(即B点、
所示。如果假定最优证券组合的收益率和方差(即B点、 点或
点或 点的坐标)分别为
点的坐标)分别为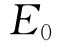 及
及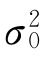 ,则将
,则将 代入极小微分法求出的
代入极小微分法求出的 解的一般式,就可求出最优证券组合中各证券组合投资比例
解的一般式,就可求出最优证券组合中各证券组合投资比例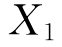 ,
, ,…,
,…, ,这就确定了最优证券组合。
,这就确定了最优证券组合。

图7.23 最优证券组合选择(1)
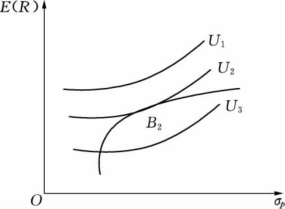
图7.24 最优证券组合选择(2)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















