低石油价格风险

（一）极值理论简述

极值理论是测量极端市场条件下风险损失的一种方法，它具有超越样本数据的估计能力，并可以准确地描述分布尾部的分位数。它主要包括两类模型：BMM模型(Block Maxima Method)和POT模型(Peaks over　Threshold)，两类模型的主要区别有：（1）极值数据的获取方法上的区别，BMM模型通过对数据进行分组，然后在每个小组中选取最大的一个构成新的极值数据组，并以该数据组进行建模；POT模型则通过事先设定一个阀值，把所有观测到的超过这一阀值的数据构成的数据组，以该数据组作为建模的对象。两个模型的共同点是只考虑尾部的近似表达，而不是对整个分布进行建模。（2）两个模型分别采用极值理论中的两个不同的定理作为其理论依据，同时也因为获取极值数据的不同方法导致两个模型分别采用不同的分布来拟合极值数据。（3）BMM模型是一种传统的极值分析方法，主要用于处理具有明显季节性数据的极值问题上，POT模型是一种新型的模型，对数据要求的数量比较少，是现在经常使用的一类极值模型。（4）BMM模型主要用于对未来一段较长的时间内的VaR和ES预测，而POT则可以进行单步预测，给出在未来一段小的时间内VaR和ES的估计值。（5）BMM模型的前提条件是样本独立同分布，POT模型的前提条件是超限发生的时间服从泊松分布，超限彼此相互独立，服从GPD(Generalized Pareto Distribution)分布，且超限与超限发生的时间相互独立。样本独立同分布可以保证POT模型的前提条件。

1.BMM模型的理论基础

假设M_n表示采用BMM方法获得的极值数据组，其中n表示每个子样本的大小，则有下面的极限定理成立。

定理1　Fisher和Tippett (1928)， Gnedenko (1943)假设(X_t)是一个独立同分布的随机变量序列，如果存在常数c_n>0，d_n∈R，以及一个非退化的分布函数H，使得 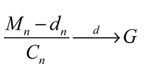成立，则分布函数G一定属于下面的三种标准的极值分布：

Frechet

（4-19）

Weibull

（4-20）

Gumbel

（4-21）

从图4-8可以清楚发现：Frechet分布用来描述那些极值无上界有下界的分布，Weibull分布用来描述极值分布有上界无下界的分布，Gumbel分布用来描述极值无上界也无下界的分布。通常见到的很多分布函数都可以根据他们尾部的状况划分到上面的三种极值分布中去。例如：学生分布、帕累托分布(Pareto distribution)、对数Gamma分布、Cauchy分布根据尾部特征可以划分到Frechet分布中去；均匀分布和Beta分布的尾部分布可以收敛到Weibull分布；正态分布、Gamma分布和对数正态分布的尾部分布都收敛到Gumbel分布。

图4-8　标准Frechet、Weibull和Gumbel分布图

但是，在实际应用中对于一个给定得极值序列，应该如何在这三种极值分布中做出选择呢？一种理想的方法是通过参数的形式把三种极值分布统一的表示成一个分布函数，这样就可以在利用最大似然估计的时候，把该参数也一块估计出来，让数据去决定它们的选择，这将极大地增加模型估计的准确性。也可以采用 Jenkinson和Mises 的方法，把三种分布表示成如下单参数的形式：

（4-22）

在定理1的基础上，对于任意一组序列，首先分组求最大值得到极值序列记为X。为了表达上的简洁，用u和σ代替公式(4-22)中的c_n和d_n，则可以序列X的近似分布函数：

（4-23）

其中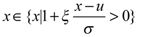，。然后，对参数进行最大似然估计，这需要得到随机变量X的概率密度函数，通过概率分布函数(4-23)对x求导，得到随机变量X的概率密度函数：

（4-24）

其中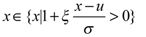，。通过似然函数就可以得到各参数的估计值：

（4-25）

在各参数估计值给定的基础上，就可以利用极值分布函数计算不同p下的分位数值，如用R^p表示这一分位数，则在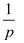个周期内出现的极值收益会超过这一阀值的预期数量有且仅有一次。R^p表达形式为：

（4-26）

2.POT模型的理论基础

假设序列{z_t}的分布函数为F(x)，定义F_u(y)为随机变量Z超过阀值u的条件分布函数，它可以表示为：

（4-27）

根据条件概率公式可以得到：

（4-28）

定理2　Pickand (1975)， Balkema和de Haan (1974)对于一大类分布F(几乎包括所有的常用分布)条件超量分布函数F_u(y)，存在一个G′_ξ，σ(y)，使得：

（4-29）

图4-9　广义Pareto分布在σ=1，ξ取0.3，0，-0.3的图形

从图4-9可以看到ξ的不同取值确定了尾部的厚度，ξ越大舞步越厚，越小则尾部越薄。从G’_{ξ， σ}（y）函数还可以得到当ξ＜０时，y的最大取值为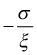，有上界。Lee和Saltoglu（2003）在金融资产收益时间序列上直接使用EVT时，由于序列的尖峰后尾，使得确定出来的ξ一定是大于零的。

根据公式（4-29）可以得到广义的Pareto分布的概率密度函数g‘ _{ξ， σ}（y）：

根据公式(4-29)可以得到广义的Pareto分布的概率密度函数

（4-30）

因此，对于给定的一个样本{z₁，…，z_n}，对数似然函数L(ξ，σ|z)可以表示为 ：

（4-31）

在POT模型中另一个重要的问题，那就是如何确定定理2中的阀值u，它的确定非常重要，它是正确估计参数ξ和σ的前提。如果阀值u选取的过高，会导致超额数据量太少，使估计出来的参数方差很大；如果阀值u选取得过低，则不能保证超量分布的收敛性，使估计产生大的偏差。Danielsson等(1997)、de Vries(1997)和Dupuis(1998)给出了对阀值u的估计方法，一般有两种：一是根据Hill图，令X₍₁₎>X₍₂₎>…>X_(n)表示独立同分布的顺序统计量。尾部指数的Hill统计量定义为：

（4-32）

Hill图定义为点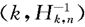构成的曲线，选取Hill图形中尾部指数的稳定区域的起始点的横坐标K所对应的数据X_k作为阀值u。二是根据样本的超限期望图，令X₍₁₎ >X₍₂₎>…>X_(n)，样本的超限期望函数定义为：

（4-33）

超限期望图为点(u，e(u))构成的曲线，选取充分大的u作为阀值，它使得当x≥u时e(x)为近似线性函数。另外，如果超限期望图当x≥u时是向上倾斜的，说明数据遵循形状参数ξ为正的GPD分布；如果超限期望图当x≥u时是向下倾斜的，说明数据来源于尾部较短的分布；如果超限期望图当x≥u时是水平的，则说明该数据来源于指数分布。这一判断方法是根据广义Pareto分布在参数ξ＞1的时候，它超限期望函数e(m)是一个线性函数。

（4-34）

注：因为对于广义Pareto分布只存在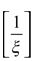阶矩，如果ξ＜1则存在一阶矩，否则一阶矩将不存在，就没有办法计算超限期望函数。

当u确定以后，利用{z_t}的观测值，根据公式(4-31)进行最大似然估计得到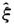 和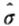 。同时，得到{z_t}的观测值中比阀值u大的个数，记为N_u，根据公(4-28)用频率代替F(u)的值，可以得到F(z)在x>u时的表达式：

（4-35）

对于给定某个置信水平p，可以由F(z)的分布函数公 式(4-35)可以得到：

（4-36）

根据GPD的条件分布函数公式(4-36)可以得到：

（4-37）

（二）BMM模型衡量石油价格低位风险

由图4-7可知，虽然石油名义价格近年来呈上涨的趋势，并且不断地创历史的新高，但通过美国通货膨胀调整的石油价格趋势来看，当前的石油价格虽然创出了历史的新高，但其维持的时间并不长，在2008年达到最高值后，又迅速下跌，目前的价格也低于1979年第二次石油价格之后的水平。并且，从近30年的情况来看，石油价格处于低价水平的时间占相当长，从1986—2004年，石油的实际价格处于低于40美元的较低水平上，虽然第一次海湾战争将石油的到岸成本推到接近2010年1月不变价格的60美元。

能源经济学的相应知识告诉我们，石油的价格是由全世界的经济增长所支撑的，当世界经济出现萧条时，石油价格将不可避免地出现下跌，但世界经济的变动是不可测的，一些意外的事件对经济体系的冲击总是超出人们的合理预测。虽然人们将当前石油价格上涨的中国因素过度地夸大，但另外一个问题是，中国的经济增长到底能够在多长时间内维持较高的水平？中国城市化进程一旦进入低速轨道，中国经济的增长速度及中国对石油需求的增长速度将出现下降，那么石油价格可能再次出现下跌。并且，其他石油需求大国如果出现大幅度的经济波动，石油价格处于低位的可能性也是存在的。

对于这些不确定性因素，我们无法进行预测，但统计学的概率分布却为我们掌握这些问题提供了一些线索。对石油价格处于低位的风险，我们首先采用区块极值(BMM)方法来研究最小石油价格和最大石油价格的极值分布。最小石油价格的极值分布对于我们了解煤化工行业的最大风险提供了线索，而最大石油价格的极值分布对于我们了解煤化工行业可能较长时间处于亏损状态提供了线索。用于分析的时间序列为图4-7中美国进口石油到岸价格的月平均价格序列，样本区间为1980年1月—2010年1月，数据来源于美国能源部能源信息局。对原始数据取自然对数值后，区块划分以年为单位，对每年分别取石油价格的最大和最小值形成两个序列。

首先，对样本数据的分布进行分析。从图4-10全样本数据的Kernel密度分布可以看出，原始数据的自然对数值呈现双峰结构。这说明石油价格主要呈现出两个稳定状态，这可能与经济发展双重均衡有关。同时，也说明要估计石油价格的水平存在着很大的困难。

图4-10　样本数据的Kernel密度分布(正态，h=0.1377)

其次，分别对区块极大值和极小值进行分布分析。极大值和极小值正态拟合的Kernel密度分布分别见图4-11，其中极小值的h=0.2303，极大值的h=0.2152。从图4-11中可以看出，极小值的分布规律性更强，极大值的双峰特征值依然显著存在。对极值进行QQ拟合，发现正态分布的拟合效果最好，其他分布都存在严重的偏离。正态分布的QQ拟合也表明极小值的分布与正态分布更为接近，而极大值与正态分布的差别更大。这说明极小值的分布规律性更强。无论从极大值还是极小值来看，肥尾现象都不存在，但低端的密度会更大一些，这与双峰结构的低端峰值大是一致的，同时也说明分布与Frechet分布更为接近。既然传统的分布无法准确地描述极值的分布状态，我们用更具普遍意义的广义极值(GEV)分布来研究极值分布状况。

图4-11　极小值(A)和极大值(B)的Kernel密切分布

图4-12　极小值(A)和极大值(B)的QQ正态拟合

第三，广义极值参数的估计。假设我们得到的极值符合广义极值分布，那么需要选择合适的ξ(形状)、μ(位置)和σ(规模)参数。对这些参数的估计需要通过最大似然估计。虽然通常人们在Eviews中选择编程求解，但Matlab的Distribution Fitting Tool工具箱却给出了参数估计的便捷方法。广义极值参数的分布估计如表4-16所示。结果表明，无论是区块极小值还是区块极大值分布的形状参数ξ都小于零，但统计上并不显著，因此分布与Gumbel分布更接近。

表4-16　BMM极小值和极大值序列广义极值参数结果

分布的拟合优度如图4-13所示。图4-13对极大值和极小值与各自的拟合分布作了Cumulative Hazard 展示。从图4-13中可以看出，极小值的分布与拟合的广义极值分布函数拟合得非常好，而极大值的分布只能说在大体上与拟合函数一致，这说明区块极小值更好地遵循广义极值分布函数。

图4-13极大值和极小值与拟合分布Cumulative Hazard展示

在得到拟合的分布函数基础上，就可以进行分位数风险衡量。利用极值分布函数计算不同p下的分位数值，如用R^p表示这一分位数，则在1　p个周期内出现的极值收益会超过这一阀值的预期数量有且仅有一次。由于这里的数据是对石油价格取自然对数值而得到的，为了进一步了解石油价格价位与分布概率之间的关系，同时列出不同分位数对应的石油价格，结果如表4-17所示。表4-17的结果表明，从最大损失的可能性来看，未来依然有50%的可能性使石油最低价格达到31美元以下，当前最低价格达到31美元时，根据表4-15所列述的煤制油项目对应的煤炭—原油价格表可知，这要求煤炭的价格不超过300元/吨。这与当前煤炭坑口价格的水平基本差不多。但由于中国未来煤炭需求量依然很大，煤炭价格上涨的趋势将会比较大，如果煤制油项目的煤炭成本继续上升，那么煤制油项目将处于亏损的状态。从区块极大值的角度来看，依然有30%的可能使得石油最大价格只有35美元，50%的可能使得石油价格最大值只有44美元，当前石油价格维持在70多美元/桶的水平上，从历史角度来看，只是处于20%的可能区间上，那么这对石油生产国而言可能只是一段幸运的时期。

表4-17极值分布条件下石油价格分布概率

(三)POT模型对价格突变的风险衡量

对美国炼油厂进口石油以不变美元(2010年1月)衡量的价格月度数据取ln值后差分，得到石油价格的月度变动数据，将该序列乘以100，得到油价波动百分比序列，见图4-14。图4-14表明，石油价格收益的月度数据不再像石油期货价格的日交易数据收益一样是稳定序列，月数据存在显著的序列相关，连续上升和连续下降的现象非常显著，这与石油价格受宏观经济基本面影响的效果是一致的。而从波动幅度来看，大部分的波动绝对值在10%以内，但也不排除大量的价格波动表现出极端变化，月度变动接近40%。石油价格的极端变动有两个方面的意义，价格极端上涨往往会对经济造成较大的冲击，而向下的极端变动则会对煤化工行业造成严重的负面影响，或者导致严重的亏损，或者使利润率出现大幅度下降，影响公司的价值。这说明，煤化工，尤其是煤制油项目，不但面临较大的石油价格水平风险，还面临较高的石油价格大幅度波动的风险。

图4-14　不变美元价格衡量的石油价格波动百分比

石油价格的月收益变动极值表现出显著的极值分布特征。在进行POT分析前，首先确定临界值。因为只有负向的石油价格波动才会对煤化工造成严重影响，正向的石油价格波动只会通过煤炭价格的联动间接地对煤化工收益造成影响，因此，我们只考察负向的石油价格波动。石油价格下降幅度分布前10%和20%分布分别如图4-15(a)、(b)所示。其中10%的阀值为-8.5251，20%的阀值为-4.6022。从序列的分布密度来看，无论是前10%的序列还是前20%的序列，都符合广义Parato分布的特征，而且存在厚尾现象。

图4-15　石油价格变动左极值分布密度

由于软件不能处理左端极值的帕累托分布，而且由于左端极值都是负值，因此需要对原数据进行转换，对L10和L20分别乘以-1，转换为正值后运用广义Parato分布进行分析。在广义Parato分布中，首先需要估计三个变量ξ和σ，并且外生决定阀值u。对于前10%和前20%的阀值根据临界值-8.5251，20%和-4. 6022来确定，对ξ和σ的估计结果如表4-18所示。从参数结果来看，两种极值的ξ估计值都是正值，但标准差比较大；而σ的估计都是统计上显著的。根据参数结果对原极值的分布情况进行拟合，可以发现，极值的概率分布与拟合的结果非常接近，但在25%~33%的波动幅度上，拟合的结果会低估实际的概率分布(见图4-16)。而且从拟合的情况来看，前10%的极值和前20%的极值分布残存函数的曲度并不一致。

表4-18　广义Parato参数估计

图4-16　10%和20%极值分布的拟合结果

但是，根据式(4-28)可以得到极值分布在原序列分布的分位数，并将累积分布分位数转换为Survivor Function形式。这意味着在前10%的极值的广义Parato极值分布中占前10%的分布在原序列中出现的概率只有1%，即在此分位数上平均每100个月出现一次。从极值序列对应的分位数及其相应在原序列中得出的分位数情况来看，对于油价下跌的极值分布情况拟合高度地一致，如在单月油价下跌达9%的幅度上，前10%的极值分布对应的原序列概率结果为9.19%，而前20%的极值分布对应的原序列结果为9.33%；而单月下跌达19.8%的幅度上，前10%的极值分布对应的原序列概率结果1.87%，而前20%的极值分布对应的原序列结果为1.80%；两个极值所得到的原序列的概率分布非常接近。这说明两个方面的问题：一、广义Parato分布对石油价格下跌的极值分布估计是正确的；二、石油价格下跌方面面临着较大的风险，单月下跌9%的可能性达到接近10%。

表4-19　原序列和前10%、20%极值序列分布Survivor Function分位数对应情况