数学课堂对话类型及其主要特征有哪些

三、数学课堂对话类型及其主要特征有哪些

既然数学课堂对话是一个“话题引发—表达倾听—回应反馈”的过程,假设将此过程作为一个有机的整体加以考察,那么数学课堂对话通常会表现出哪些类型,不同的数学课堂对话类型又分别具有怎样的特征呢?下面,试图对此问题作出理性的回答。

(一)数学课堂对话类型划分的逻辑依据

本研究表明,职初教师、有经验教师和骨干教师在数学课堂对话的语言特征和意义特征上都表现出比较明显的差异,在教师倾听与回应学生的方式上差异表现尤为突出。这三类教师的数学课堂对话特征主要表现为:

职初教师倚重于简单的“师问生答”,虽然鼓励学生参与对话过程,但以教学预设作为唯一杠杆,以评价性倾听和一般性追问推进对话,以教师澄清和传递数学知识作为对话目的;学生以听讲为主,在教师规约下配合教师提供简单的答案,真正参与数学理解和数学意义建构的心智水平并不高。

有经验教师虽然开始关注学生,能以学生话语中的数学想法作为支架来推进对话,但仍带有较强的“引导性”,以解释性倾听和试探性追问逐步推进对话,表现出较好的对话性;学生在教师“帮”“扶”下,参与数学理解和数学意义建构过程中表现出中等程度的心智水平。

骨干教师重视唤醒学生已有的经验,提供机会让学生充分表达和暴露各种数学见解和疑惑,以更民主的移情性倾听、探索性和开放性追问等方式推进教学,鼓励学生在协商论辩和互动交往中达成数学共识;学生学习主体地位得到充分发挥,在参与数学理解和数学意义建构中表现出较高的心智水平。

由此可见,数学课堂对话总是围绕着“明线”和“暗线”展开的。“明线”是指以外显的表达、倾听、回应等师生口头话语的互动,“暗线”是指对话推进学生参与数学学习的思维深度。为此,数学课堂对话促进学生数学思维水平的程度,应作为划分数学课堂对话类型的逻辑依据。

(二)数学思维层次说

数学是一门研究数量关系和空间形式的科学,具有严密性、抽象性和逻辑性强等特征。什么是数学思维(mathematical thinking)?有人认为是“应用数学工具解决各种实际问题的思考过程,”^[7]也有人认为是“数学活动中的思维,即研究人脑对数学学科的客观事物(如定义、公式、定理、法则)的本质属性与规律性联系的反映,”^[8]更有人认为是“人们对数学对象间关系的反映。”^[9]的确,数学思维是一个相当复杂的心理现象,至今尚未形成统一的定义。正如罗伯特·斯腾伯格(R.J.Sternberg)所言,“就像游戏那样,似乎不可能用一组必要且足够的定义性特征来精确界定‘数学思维’这个概念,我们只能讨论与之相关的一些核心要素”。^[10]

我们这里所指的“数学思维”是从教育学角度着眼,类似于日常所言的数学思考。它主要指如何通过教育的作用,改善人们的数学思维水平和层次,提高解决数学问题的能力,提升创造性思考及协商形成数学学习共同体的能力。

在众多“思维”分类框架中,最知名的当属布鲁姆的思维分类说。布鲁姆将思维由低到高、由简单到复杂、由具体到抽象分成六个层次,依次为知识(Knowledge)、理解(Comprehension)、应用(Application)、分析(Analysis)、综合(Synthesis)和评价(Evaluation)。^[11]前三个层次属于较低层次的思维水平,而后三个层次则属于较高层次的思维水平。

数学思维层次是对数学思维深度所进行的水平划分。受布鲁姆思维分类说的影响,国际上出现了多种数学思维层次观。下面列举几个具有代表性的观点:

1.美国各州首席教育官员理事会(CCSSO)将中小学的数学认知领域划分为五个水平:①记忆事实、定义、公式;②实施程序;③说明和解释数学的思想;④猜想、一般化、证明;⑤联结与解决非常规问题。^[12]

2.美国匹兹堡大学主持的以促进学生数学思维、推理和问题解决能力为目标的数学教学改革研究项目QU ASAR(Quantitative Understanding: Amplifying Student Achievement and Reasoning)分析框架中,把数学认知划分为“记忆、无联系的程序、有联系的程序和做数学”四个水平。^[13]

3.我国学者顾泠沅及其研究团队,采用主成分分析法构建了数学认知的两个水平四个层次的数学思维框架:较低水平包含计算/操作性记忆、概念/概念性记忆两个层次,较高水平包含领会/说明性理解、分析/探究性理解两个层次。^[14]其中,较低水平的两个记忆层次都旨在识别和记住事实性材料,重在机械模仿便于再认或再现。说明性理解层次以教师活动为主,旨在变换角度讲解和解释知识,以便让学生理解领会和在新情境中应用新知。探究性理解层次以学生活动为主,旨在引起认知冲突让学生参与数学问题提出、探究和解决的过程。

4.著名数学教育研究者韬尔(D.Tall)基于不同的数学内容构建了数学思维发展基本框架(见图6-5)^[15]。韬尔认为,从最基本的“与环境互动”出发,沿着“几何表象”和“代数过程性概念”两条不同的认知途径,数学思维从初等思维过渡到高等思维,由低到高实现“感知(行动)→表象(过程性概念)→形式化→创造性思维”的逐级发展。过程性概念由易到难可分为操作性的过程性概念(如算术概念和公式等含有明确算法的概念)、模式化的过程性概念(如代数式等可任意赋值的变量)和结构性的过程性概念(如极限等通过关系结构去发现结果的过程)三个层级。由此,韬尔指出,数学思维中存在着动作性、图像性和符号性三种心理表征系统,且各表征系统中又可细化为具体的行动、对象与证明(见图6-6)^[16]。从图中可见,具体可采用一些动词来描述数学思维过程:感知、操作、描述、解释、运算、推理、实验、验证、证明、定义和符号化等。类似地还可用以下词汇描述数学思维,如表征、概括、分类、联结、归纳、分析、综合、抽象、可视化^[17]和公式化等。

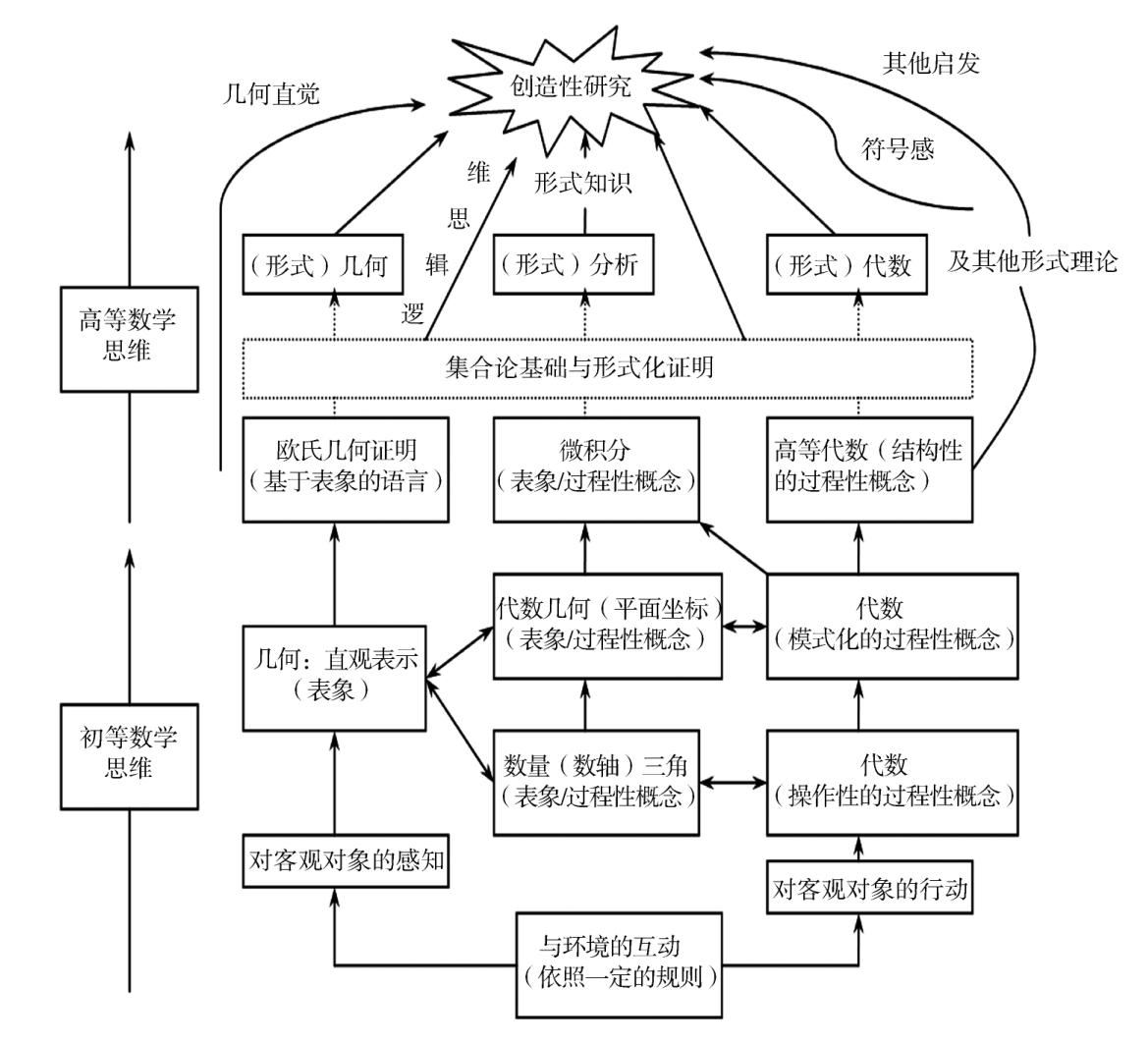
图6-5　基于课程内容的数学思维发展框架(韬尔,1995)

图6-6　数学思维三种不同心理表征系统中的行动、对象与证明

综上所述,虽然不同学者对“数学思维”概念的分类不一,但从中反映出了共同具有的一些的核心要素,即由低到高包含记忆、理解、探究和创造四大要素。记忆是数学思维的前提,理解是数学思维的关键,探究是数学思维的根本,创造是数学思维的最高层次。为此,本研究将数学思维由低到高分成记忆性思维、理解性思维、探究性思维和创造性思维四个水平。记忆性思维水平是最低水平,指记住数学事实、定义、公式和操作程序等;理解性思维水平指学生依赖教师讲解来领会与理解数学概念、关系和原理等;探究性思维水平指运用猜想、实验、证明等方法综合性地探索数学知识和解决数学问题;创造性思维水平是最高水平,指批判性地整合数学知识解决非常规的数学问题,并作出负责任的解释。

(三)数学课堂对话类型的划分

依据数学课堂对话的内容属性不同,本研究将数学课堂对话划分成学术性对话、非学术性对话和无关对话三个大类。其中,学术性对话侧重于认知维度,是数学课堂对话的主体;非学术性对话侧重于情感和行动维度,无关对话是指与教学主题没有本质关联或相偏离的数学课堂对话。

依据“对话促进学生数学思维水平的程度不同”,以及将数学思维分为记忆性、理解性、探究性、创造性四个水平的分类观点,我们将数学课堂学术性对话又划分成检测性对话、理解性对话、探究性对话和批判性对话四种类型。依据对话内容与教学目标关系的性质不同,数学课堂非学术性对话又可划分为情感性对话、课堂组织管理性对话两种类型。由此,数学课堂对话包括学术性对话(检测性对话、理解性对话、探究性对话和批判性对话)、非学术性对话(情感性对话、课堂组织管理性对话)和无关对话三个大类七个子类(见图6-7)。

图6-7　数学课堂对话类型

所谓检测性对话,指向记忆性数学思维水平,由教师控制对话内容和进程,旨在口头检查与监测学生是否记住了已学知识或是否提供了正确答案,通常由“这是什么”“看见了什么”“已学过……你会吗”等识记性或封闭性的问题引发,学生仅凭回忆或经验或直观就可以作出回答,伴有“师问生答”或“师问生答与教师评价”等直线式的对话形式。如下三种情况下发生的课堂对话,通常属于检测性对话:①检查是否掌握和记住了已学知识;②考查能否直接运用已知公式解题;③要求凭直观简单地描述数学事实或数学现象等。例如,

师:我们学过了长方形的面积公式,它是怎么求的呢?

生:长方形的面积等于长乘以宽。

师:很好。

所谓理解性对话,指向理解性数学思维水平,由教师主导,旨在推动学生个体对所学知识的领会理解和对简单解题策略的澄清,通常由“你是怎么想的”“为什么”“请说明理由”“谁能解释××的想法是什么意思”等描述性和解释性的问题引发,答案具有预设性且思维过程由单一的封闭性转换而得以实现,多伴有“教师提问—学生陈述”或“教师提问—学生陈述—教师追问”等对话形式。常见的情况有:①要求学生尝试用自己的话语描述、概括和解释所学的新知;②要求学生澄清简单的解题策略和思维过程;③鼓励学生对他人想法进行理解性的解说与澄清等。例如,

师:有3件上衣和2件裙子,如果要求一件上衣配一条裙子,那么会有几种搭配方案?(稍后)张同学,你来说一说你是怎么做的?

张:这件红色衣服可配粉色的裙子和绿色的裙子,黄色衣服可以配粉色的和绿色的裙子,蓝色衣服也可以配粉色的和绿色的裙子,这样总共有6种搭配方法。

所谓探究性对话,指向探究性数学思维水平,旨在激发学生多维度探求数学问题解决的策略,通常由“为什么”“有什么问题”“还有什么不同观点”“这两种方法有什么不同”“如果……怎么办”等开放性和探索性的问题引发,问题解决方案多样化且思维过程实现开放性转换,重在陈述多种观点。常见的情况有:①学生针对教师所提的问题,进行开放性思维和多角度地探究问题解决的方案;②分析和探究深层次的数学规律;③提出猜测性假设并加以验证;④教师启发学生提问等。例如,

师:如果要在小丁、小巧、小亚和小胖四人中选两人参加数学比赛,有几种选法?

生1:因为要从4人中选出2人,有3种选法,但里面会出现重复,所以应该是3乘4除以2等于6种(3×4÷2= 6),总共有6种选法。

生2:我还有一种方法,小丁可以配小巧、小亚、小胖,小巧可以配小亚、小胖,小亚可以配小胖,所以我认为是3加2加1(3+ 2+ 1),也是6种。

师:可以吗?仔细看看这两种方法有什么不同?

所谓批判性对话,是对话的最高境界。指向批判性和创造性数学思维水平,旨在鼓励学生质疑和挑战权威,开展批判性的论辩,解决数学问题或生成数学结论,以学生的想法推进对话进程,常伴有生生与生师多向交互的对话形式。通常由“有没有不同意见”“你认为哪种方法更好,为什么”“他不同意你的观点,怎么办”等反思批判性的问题引发,鼓励不同观点之间产生挑战与反挑战,对自己或他人观点做出负责任的解释,从而形成数学话语共同体。与探究性对话不同的是,批判性对话更强调不同观点之间的互动。常见的情况有:①学生对教师或同伴或课本的观点提出质疑;②学生对有争议或疑难的问题展开讨论;③不同观点之间的挑战与反挑战;④选择最佳方案并分析缘由;等等。例如:

师:什么是圆的“直径”?

生1:把圆上一点和它对面一点连起来就是直径。

生2:我有疑问。如果不经过圆心怎能画出直径?

师(对着生1):你回答他。

生1:直径就是从这边半径到那边半径的合并。

生2(针锋相对):你刚才说从圆上一点到圆上另一个点,没说要经过圆心,也没说什么两个半径的合并。

生1:(显得有些着急,边作比画边说)圆的直径就是圆的垂直线段。从这头到那头的垂直线段就是直径。

师:垂直线段?我也晕了。我看你的手势好像是说像这样斜的就不是直径了,对吗?

生1:也是直径。

师:好,我把你刚才说的画下来。请看这个图,圆上一点A,对面一点B,这也是对面,对吗?

生1:不是,对面那点指的是经过圆心的那个点。

生2:可是刚才你没说要经过圆心。

师(对着生1):你现在能说什么是直径了吗?

生1:直径就是经过圆心的两条半径的合并。

师:经过圆心,直径是线段,也有两个端点。两个端点在哪?我明白大家的意思。我们可以这样来表达:通过圆心并且两端都在圆上的线段叫作圆的直径。

所谓情感性对话,侧重从情感维度划分,指师生之间所进行的与兴趣、信心、动机等情绪情感相关的对话。例如,

师:我再叫一个来说,看看她讲的和你讲的一样不一样?你来。

生:先……再……(具体内容省略)

师:好。真的理解了,你们两个说得都很不错。我们一起为她们两位鼓鼓掌。

生(齐鼓掌)。

所谓课堂组织管理性对话,侧重从行动维度划分,指为维持教学组织和程序而展开的管理性对话。通常表现为两种情况:①维持良好的课堂行为规范所发生的对话。例如,师:身坐正。生(齐):脚放平。②两个教学环节进行转换而发生的过渡性对话或有关读写做等行为的指令性对话。例如,

师:下面我们在位值图上摆一摆。听清楚老师的要求,不需要的小圆片放在杯子里。听明白了吗?

生(齐):听明白了。

师:好,下面开始。

所谓无关对话,指与教学主题没有本质关联或相偏离的师生对话。例如,

师:我们快要下课了。小巧讲故事比赛也结束了。你们知道她获得了几等奖吗?

生:一等奖。

师:哇。你们怎么都那么聪明啊。一等奖的奖品很丰厚,有溜冰三件套:帽子、护膝和鞋子。

【注释】

[1]Shulman,L.S.(1999).Taking learning seriously.Change,31(4): 11-17.

[2]喻平编著.数学教学心理学[M].北京师范大学出版社,2010(1):50-59.

[3]Sawyer.K.K.(2006).The Cambridge handbook of the learning sciences.New York: Cambridge University Press.

[4]Black,P.,＆ William,D.(1998).Assessment and classroom learning.Assessment in Education:Principles,Policy＆ Practice,5(1):7-75.

[5]Pirie,S.E.B.,＆ Kieren,T.E.(1992).Watching Sandy's understanding grow.The Journal of Mathematical Behavior,11(3):243-257.

[6]鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009:4-5,7.

[7]王仲春,等.数学思维与数学方法论[M].北京:高等教育出版社,1989.

[8]郭祖仪.对心理学中思维定义的质疑与探讨[J].陕西师范大学学报(社科版),1990(2).

[9]李三平.关于数学思维[J].数学教育学报,1996(1):17-19.

[10]R.J.Sternberg.What is Mathematical Thinking?In Robert J.Sternberg＆ Talia Ben-Zeev.(1996).The Nature of Mathematical Thinking.Lawrence Erlbaum Associates,Inc.pp.303-304.

[11]Bloom,B.,Englaehart,M.D.,Furst,E.J.,Hill,W.H.,＆ Krathwohl,D.R.(1956).A taxonomy of educational objectives,handbook 1:The cognitive domain.New York: David Mc Kay.

[12]鲍建生,周超.影响学生高层次数学认知能力的因素分析[J].中学数学月刊,2010(9):1-4.

[13]Henningsen,M.＆ Stein,M.K.,(1997).Mathematical Tasks and Student Cognition: Classroom-Based Factors That Support and Inhibit High-level Mathematical Thinking and Reasoning.Journal for Research in Mathematics Education.Vol.28,No.5,524-549.

[14]青浦实验小组.学会教学[M].北京:人民教出版社,1991.

[15]David Tall.(1995).Cognitive Growth in Elementary and Advanced Mathematical Thinking.Plenary Lecture,Conference of the International Group for the Psychology of Learning Mathematics,Recife,Brazil,July 1995,Vol I,pp.161–175.

[16]鲍建生,周超.数学学习的心理基础与过程[M].上海:上海教育出版社,2009:64.

[17]笔者注:可视化(visualizing)是指抽象概念的可视化过程,以此建立“表象”和“过程性概念”之间的联系。