实数的逼近

上面已经提到为了建立严格的无理数基础，众多的数学家耗费了他们的心血。到19世纪下半叶时，人们终于明白了有理数与无理数的本质区别。然而，当我们从实用的角度出发时，却会发现这种区别是毫无意义的。从这一角度看的话，有理数与无理数之间没有真正的区别，因为我们在对数字进行书写和计算时，只进行到有限多位。这就是说，我们可以在无理数的某些数位之后，截掉后面无尽的数位，而得到该数的一个近似值。想想看，我们所用的数学用表中的无理数不都是取的近似值吗？因此，对于应用数学的工程师等而言，他们很少关心一个物体的长度是有理数还是无理数，因为即便该长度是无理数，由于所有的测量装置都具有不完美性，也由于根本没有这种必要。他们在任何情况下以有限的精确度对其进行测量就够了。这大约正是数学的理论与应用之间的最大差别之处。

从实用角度来说，还会产生一个我们前面已经提到过的重要问题，即给定实数，找一个有理数去逼近它。由于实数的有理逼近问题，可表为求某种不等式的整数解问题。而在整数范围求解的不定方程人们往往称为丢番图方程。于是这门关于实数有理逼近问题的分支被称之为丢番图逼近论。

事实上，人们很早就产生了有理逼近的思想，用较简单的有理数来逼近、表示某些数，是数学中传统的做法。

如：公元前3000年左右，巴比伦人就已造出平方根表和立方根表，其中用1.414213或17／12表示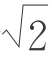。而前面一章我们详细叙述的求圆周率的历史，实际上也就是对无理数π作有理逼近的历史。还可以指出，丢番图逼近与连分数有密切联系。一个数的连分数展开，往往就是具体构造有理逼近解的过程。

当然，这些还都是些个别的工作，真正系统的逼近理论是在19世纪中叶开始的。

这种研究包括：在得到一个数的逼近后，考虑逼近的量（通常是有理数）与被逼近的量（通常是无理数）之间的误差是多少。通过误差的大小，来了解逼近的好坏。好坏有了标准，随后的问题便是得到最佳逼近。最佳逼近是否存在以及存在多少，这样的问题就不仅仅是实际操作问题而是指导操作的理论问题了。

此外，1844年，刘维尔还开创了实代数数的有理逼近的研究。正是在这一研究中，他发现代数数与超越数的一大区别，即超越数能被有理数很好地逼近，而代数数则不能，并由此出发构造出历史上的第一个超越数。

时至今日，丢番图逼近仍是数论中一个活跃的与应用广泛的分支。事实上，实际工作和理论研究中，绝大多数的数值计算问题，都是用逐次逼近法解决的。数学中有各种各样的逐次逼近法。用这种思想方法处理问题，不仅在数学中十分广泛，在其他科学领域里也是极为广泛的。因而，这是一种普遍的思想方法。现在电子计算机的广泛使用又提供了具体实现逐次逼近的有力工具。因而现在逐次逼近的方法被广泛地用于科技工作中遇到的计算问题中。