牛顿型流体与牛顿粘性定律

第5章　描述流体相及气固两相流动的基本方程

5.1　流体与流动的基本特征

5.1.1　理想流体与粘性流体

粘性（viscocity）是流体内部发生相对运动而引起的内部相互作用。

流体在静止时虽不能承受切应力，但在运动时，对相邻两层流体间的相对运动，即相对滑动速度却是有抵抗的，这种抵抗力称为粘性应力。流体所具有的这种抵抗两层流体间相对滑动速度，或普遍说来抵抗变形的性质，称为粘性。

粘性大小依赖于流体的性质并显著地随温度而变化。实验表明，粘性应力的大小与粘性及相对速度成正比。当流体的粘性较小（如空气和水的粘性都很小），运动的相对速度也不大时，所产生的粘性应力比起其他类型的力（如惯性力）可忽略不计。此时，我们可以近似地把流体看成无粘性的，称之为无粘流体（inviscid fluid），也可称之为理想流体（perfect fluid）。而对于有粘性的流体，则称之为粘性流体（viscous fluid）。十分明显，理想流体对于切向变形没有任何抗拒能力。应该强调指出，真正的理想流体在客观实际中是不存在的，它只是实际流体在某种条件下的一种近似模型。

5.1.2　牛顿型流体与牛顿粘性定律

当流体流动时，流体内部存在着内摩擦力，这种内摩擦力会阻碍流体的流动，流体的这种特性称为粘性。一维分层流动中，两相邻流体层之间的单位面积上的内摩擦力（实际上是表面力中的切应力，又称剪应力，用τyx表示）与两流体层间的速度梯度成正比，即

此式称为牛顿关于流体粘性的内摩擦定律。服从此定律的流体称为牛顿型流体，所有的气体和大部分低分子量（非聚合的）液体或溶液均属于牛顿型流体。

式（5－1）中的比例系数μ称为动力粘度，常简称为粘度，其物理意义是速度梯度为1时，单位受力面积上流体层之间内摩擦力的大小。它的值取决于流体的性质、温度和压力大小，μ的单位是Pa·s。显然，流体粘度是衡量流体粘性大小的一个物理量，它不仅影响流体运动的形态和性质，而且也影响流体运动中许多物理量的数值。

5.1.3　非牛顿型流体

凡是剪应力与速度梯度不符合牛顿粘性定律的流体均称为非牛顿型流体。一般而言，浓稠的悬浮液、淤浆、乳浊液、长链聚合物溶液、生物流体、液体食品、涂料、粘土悬浮液以及混凝土混合物等均为非牛顿型流体。

非牛顿型流体的剪应力与速度梯度成曲线关系，或者成不过原点的直线关系，如图5－1所示。非牛顿型流体可以分为三大类：第一类是流体的剪应力与速度梯度间的关系不随时间而变，图5－1所示的均属于此类；第二类是流体的剪应力与速度梯度间的关系与时间有关，但为非弹性的，这类流体的现时性质与它最近受过什么样的作用有关，例如番茄酱放着不动会倒不出来，然而一瓶刚刚摇过的番茄酱就容易倒出来；第三类是粘弹性非牛顿流体，这类流体兼有固体的弹性与流体的流动特性，应力除去后其变形能够部分地恢复，例如面团受挤压通过小孔而成条状后，面条的截面积略大于孔面积。

目前在工程应用上对非牛顿型流体的研究主要集中在第一类，本节仅对这类非牛顿型流体作一简单介绍。

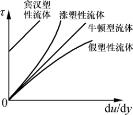
图5－1　剪应力与速度梯度的关系

5.1.3.1　宾汉塑性流体（Bingham－plastic　fluid）

此类流体的剪应力与速度梯度呈线性关系，但直线不过原点（见图5－1），即?

这个关系表示剪应力超过一定值后流体才开始流动，其解释是此种流体在静止时具有三维结构，其刚度足以抵抗一定的剪应力。当剪应力超过该数值后，三维结构被破坏，于是流体就显示出与牛顿型流体一样的行为。属于此类的流体有纸浆、牙膏、岩粒的悬浮液、污泥浆等。

5.1.3.2　假塑性流体（pseudo－plastic　fluid）和涨塑性流体（dilatant　fluid）

这两类流体的剪应力与速度梯度符合指数规律，即

式中，n为流变指数（flow　behavior　index），无因次；K为稠度指数（consistency　index），单位为Pa·sn。n、K均需由实验确定。对于假塑性流体，n＜1；对于涨塑性流体，n＞1；对于牛顿型流体，n＝1。

与牛顿粘性定律相比，式（5－3）又可写成

其中称为表观粘度。

本章以下所介绍的描述单相及气固两相流动的基本方程均按牛顿型流体建立。对于非牛顿型流体，如稠密气固两相流动，随着固相浓度的增加，其固相流动特性将逐步偏离牛顿型流体，需要对基本方程做相应的修正。这方面的工作读者可另查阅相关文献。

5.2　流体动力学控制方程

5.2.1　连续性方程

根据质量守恒定律，流场中任意形状的一个控制体中流体质量对时间的变化率与流经该控制体表面的净质量流量在数值上完全相等，即

或

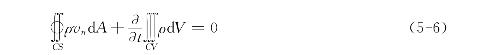
式中，A是控制体的表面积，V是控制体的体积。控制体可以是流场中任意形状的封闭体。保持流体呈连续流动状态而得到的连续性方程式，是一切流体运动所必须遵循的一项普遍原则。以直角坐标系为例，现推导流场中任一点的连续性方程。

设把流场中任一边长为dx、dy和dz的微元平行六面体作为控制体，如图5－2所示。微元平行六面体的形心坐标为x、y、z，在某一瞬时t经过形心的流体质点的速度沿三个坐标轴的分量为vx、vy、vz，密度为ρ。现将积分形式的连续性方程式（5－6）应用于该控制体。

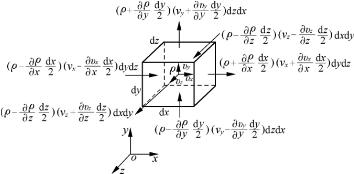
图5－2　推导微分形式的连续性方程

沿x轴方向从左面微元面积dydz上每秒流入的流体质量为

从右边微元面积dydz上每秒流出的流体质量为

于是沿x轴方向每秒流出的流体质量和流入的流体质量之差为

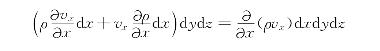
同样可得，沿y轴和z轴方向每秒流出的流体质量和流入的流体质量之差分别为

因此，每秒流出微元六面体和流入微元六面体的流体质量之差为

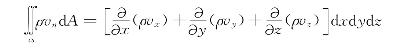
微元控制体内密度变化引起的每秒流体质量的变化为

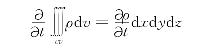
代入式（5－6）并除以dxdydz，得

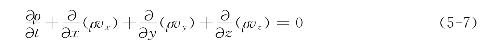
当流出的流体质量大于流入的流体质量时为负，微元体内的密度随流体质量的减少而减小；反之，当流出的流体质量小于流入的流体质量时为正，微元体内的密度随流体质量的增多而增大。这就是可压缩流体非定常三维流动微分形式的连续方程，也可写成矢量形式

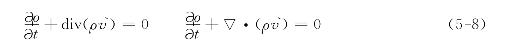
对于可压缩流体的定常流动，，得

对于不可压缩流体的定常或非定常流动，ρ等于常数，式（5－9）简化为

这表示，不可压缩流体流动时，三个轴向速度分量沿各自坐标轴的变化率互相约束，不能随意变化。很明显，式（5－10）又指出，在流动过程中不可压缩流体的形状虽有变化，但体积却保持不变。

对于二维定常流动，式（5－9）和式（5－10）变为

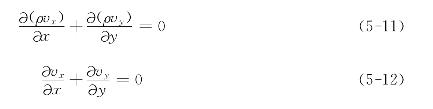
5.2.2　动量守恒方程

动量守恒定律是任何流动系统都必须满足的基本定律。该定律可表述为：微元体中流体的动量对时间的变化率等于外界作用在该微元体上的各种力之和。

当粘性流体运动时，粘性的影响产生了切向应力。因此，在研究粘性流体运动时，除了质量力和法向应力外，还要考虑切向应力。

在运动着的粘性流体中取出一边长为dx、dy和dz的平行六面体的流体微团（图5－3），作用在平行六面体上的表面力不仅有法向应力，还有切向应力，这些力在每个表面上的合力不再垂直于所作用的平面，而与作用面成某一倾角。图中p代表法向应力，τ代表切向应力，它们都有两个下标，第一个表示应力所在平面的法线方向，第二个表示应力本身的方向。为方便起见，假定所有法向应力都沿着所在平面的外法线方向，切向应力在经过A（x，y，z）点的三个平面上的方向与坐标轴的方向相反，其他三个平面上的则相同。

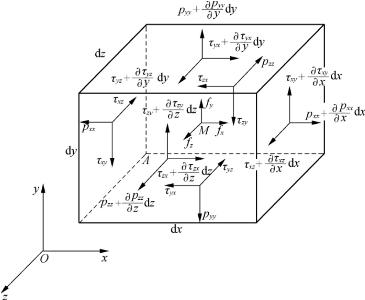
图5－3　推导不可压缩粘性流体运动微分方程用图

根据牛顿第二定律，可写出沿x轴的运动微分方程

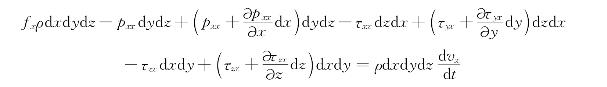
化简后得

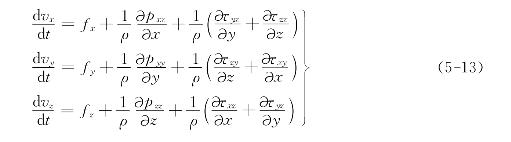
式（5－13）是以应力形式表示的粘性流体的运动微分方程。式中除了单位质量力的3个分量fx、fy、fz以及密度ρ在一般不可压缩粘性流体运动中为已知数外，其余9个应力和3个速度分量都为未知数，而方程除了这3个外，再加上连续方程，只有4个，远不足以解出这12个未知数。现在的问题是，要寻找粘性流体中关于p和τ的计算式。我们可以从流体微团在运动中的变形来获得这些应力与应变速度之间的关系式。

首先研究切向应力之间的关系。根据达朗伯原理，作用于微元平行六面体上的各力对通过中心M并与z轴相平行的轴（图5－4）的力矩之和应等于零。又由于质量力和惯性力对该轴的力矩是四阶无穷小量，可以略去不计，故有

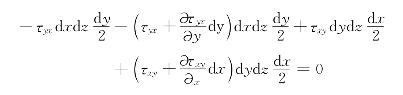
再略去四阶无穷小量，又因dxdydz≠0，故得

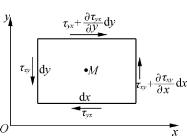
图5－4　分析切向应力之间的关系用图

同理可知

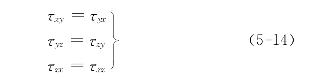
这样，在式（5－13）中9个应力只有6个是独立的。

在5.1节中已经指出过，当粘性流层间发生相对运动时，流体粘性引起的切向应力可按牛顿内摩擦定律公式（5－1）求得，即

而速度梯度又等于流体微团的角变形速度，即

流体微团的角变形速度为

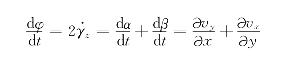
假若流体的粘度在各个方向上都是相同的（即各向同性），则根据牛顿内摩擦定律，可得

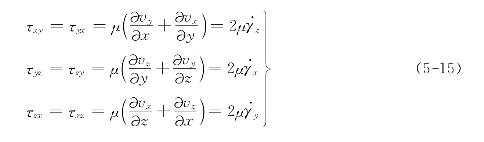
式中为垂直于各相应轴的平面中角变形速度之半。式（5－15）就是广义牛顿内摩擦定律，其意义为：切向应力等于动力粘度和角变形速度的乘积。

现在研究法向应力之间的关系。对于理想流体，在同一点各方向的法向应力（即压强）是等值的，即pxx＝pyy＝pzz＝－p。但是粘性流体中，由于粘性的影响，流体微团除发生角变形 以外，同时也发生线变形，即在流体微团的法线方向上有相对的线应变速度，使法向应力的大小有所改变（与理想流体相比），产生附加的法向应力。在此不作严格的推导，而将切向应力的广义牛顿内摩擦公式推广应用，即认为附加法向应力等于动力粘度与线应变速度的乘积的两倍。因此得

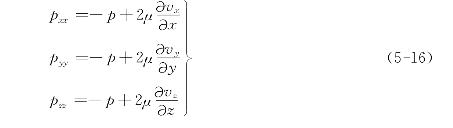
这就是法向应力的计算式。由此可见，在粘性流体中同一点任意三个互相垂直的法向应力是不相等的，它们的总和

根据不可压缩流体的连续性方程式（5－10），上式等号右边第二项为零，故得

这说明三个互相垂直的法向应力的算术平均值恰好等于理想流体的压强。

现在将切向应力和法向应力的关系式（5－15）和式（5－16）代入式（5－13），仅以第一式为例，得

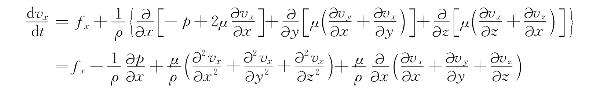
根据不可压缩流体的连续性方程式（5－10），上式等号右边第四项为零，故得

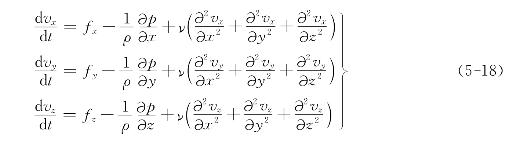
这就是不可压缩粘性流体的运动微分方程，又称纳维－斯托克斯（Navier－Stokes）方程（简称为N－S方程）。如果是没有粘性的理想流体，则ν为零，于是纳维－斯托克斯方程变成理想流体的欧拉运动微分方程。如果没有加速度，则都为零，于是上述方程变成欧拉平衡微分方程。所以说，上述纳维－斯托克斯方程是不可压缩流体的最普遍的运动微分方程。

以上3式加上不可压缩流体的连续方程

共有4个方程，原则上可以求解不可压缩粘性流体运动问题中的4个未知数vx、vy、vz和p。但是，实际上由于流体流动现象很复杂，要利用这4个方程去求解一般不可压缩粘性流体的运动问题，在数学上还是很困难的。所以，求解纳维－斯托克斯方程仍然是流体力学的一项重要任务。许多层流问题，如圆管中的层流、平行平面间的层流以及同心圆环间的层流等，都可以应用纳维－斯托克斯方程求出精确解。此外，对于润滑问题、边界层问题等，也可以应用该方程求出一些近似解。近年来应用纳维－斯托克斯方程去求解紊流问题也取得了一定的进展。

在求解许多实际流动问题时，例如粘性流体绕过圆柱体和球体的流动，用圆柱坐标系（r、θ、z）和球坐标系（r、θ、β）来代替直角坐标系（x、y、z）会更为方便。变数经过变换后，可将直角坐标系的纳维－斯托克斯方程写成圆柱坐标系和球坐标系的纳维－斯托克斯方程。略去变换步骤，将结果写出如下：

在圆柱坐标系中

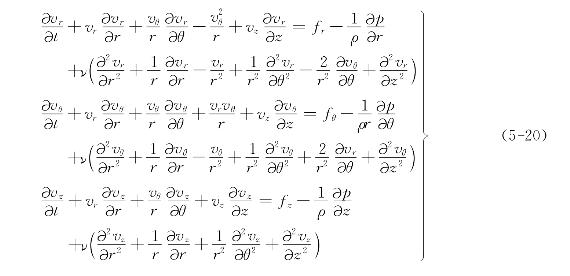
式中fr、fθ和fz为单位质量的质量力沿三个坐标轴（r，θ，z）的分量。不可压缩流体的连续性方程为

法向应力和切向应力的公式分别为

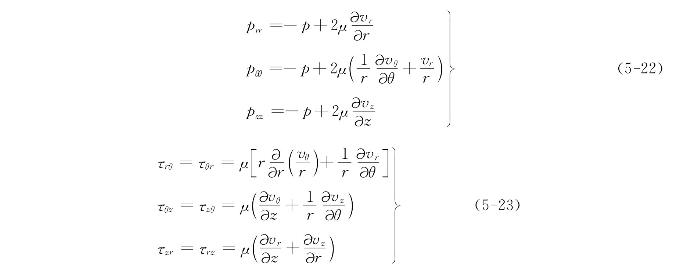
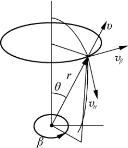
图5－5　球坐标系

在球坐标系中（见图5－5）

式中fr、fθ和fβ为单位质量的质量力沿三个坐标轴（r、θ、β）的分量。不可压缩流体的连续性方程为

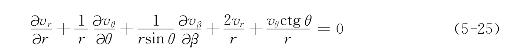
法向应力和切向应力的公式分别为

理论上，通过求解由连续性方程、运动方程以及流体的状态方程f（ρ，p，T）＝0等5个方程组成的偏微分方程组，再结合具体过程的初始条件和边界条件，可获得速度场、压力场和密度场。但事实上，由于方程组中含有非线性项［如式（5－11）中ρvx对x的导数］，使求解过程十分困难。到目前为止，只有极少数几个简单问题得到了解析解。例如：

（1）对于某些特定的流动问题，N－S方程中若干项将等于零，从而使方程大大简化，由偏微分方程组转化为一个常微分方程。典型的例子是圆管内的层流流动问题、环隙内流体层流流动问题等，此时可得到其精确解。

（2）当方程中的某些项相对于其他项可以略去不计时，也可使N－S方程简化而求出其近似解。例如，对于Re＜1的极慢流动（又称爬流），惯性力相对于粘性力来说可以略去不计，此时方程的求解就简单很多。

（3）对于雷诺数很大的实际流体绕物体的流动，可以将流体分为两个区域，一个是靠近壁面的边界层区域（指壁面附近速度变化较大的区域），另一个是边界层以外的外流区域（指速度变化很小的区域）。外流区域的流体可以看作理想流体而用欧拉方程来计算。至于边界层内的流动，则可根据边界层理论对N－S方程进行若干简化而求其近似解。

对于复杂流体流动问题，可采用数值流体力学的方法求解。数值流体力学不仅可解决层流问题，而且已成功应用于解决许多湍流问题。读者可参阅有关专著。

5.3　湍流流动

湍流流动是自然界常见的现象，在多数工程问题中流体的流动往往处于湍流状态，湍动特性在工程中占有重要的地位，湍流研究一直被研究者高度重视。然而，由于湍流本身的复杂性，直到现在对湍动特性的研究远未成熟，仍有一些基本问题尚未解决。本书主要介绍不可压流体湍流流动的常用数值模拟方法。

5.3.1　湍流流动的基本特征

流体试验表明，当流体流动的雷诺数小于某一临界值时，流动是平滑的，相邻的流体层彼此有序地流动，即为层流（laminar flow）。当雷诺数大于临界值时，会出现一系列复杂的变化，导致流动特征发生本质的变化，流动呈无序的混乱状态。这时，即使边界条件保持不变，流动也是不稳定的，速度等流动特性都随机变化，这种状态即为湍流流动（turbulent flow）。

从物理结构上看，可以把湍流看成由各种不同尺度的涡（eddy）叠合而成的流动。这些涡的大小及旋转轴的方向分布都是随机的。大尺度的涡主要由流动的边界条件决定，其尺寸可以和流场的大小相比拟，它主要受惯性影响而存在，是引起低频脉动的原因；小尺度的涡主要由流体粘性而决定，其尺寸可能只有流场尺寸的千分之一的量级，是引起高频脉动的原因。大尺度的涡破裂后形成小尺度的涡，较小尺度的涡破裂形成更小尺度的涡。在充分发展的湍流区域内，流体涡的尺寸可在相当宽的范围内连续变化。大尺度的涡不断地从主流获得能量，通过涡间的相互作用，能量逐渐向小尺度的涡传递。然后由于流体粘性的作用，小尺度的涡不断消失，机械能就转化（或称耗散）为流体的热能。最后由于边界条件的作用、扰动及速度梯度的作用，新的涡又不断产生，这就构成了湍流运动。流体内不同尺度的涡的随机运动造成了湍流的一个重要特点——物理量的脉动。

5.3.2　湍流基本方程

无论湍流运动多么复杂，非稳态的连续性方程和N－S方程对于湍流的瞬时运动仍然是适用的。为了考虑脉动的影响，目前广泛采用的方法是时间平均法，即把湍流流动看作由两个流动叠加而成，一是时间平均流动，二是瞬时脉动流动。这样将脉动分离出来会便于处理和进一步的探讨。引入雷诺（Reynolds）平均法，任一变量φ的时间平均值定义为

这里，上标“－”代表对时间的平均值。若用上标“′”则代表脉动值，物理量φ的瞬时值可表示为

将式（5－29）代入瞬时状态下的连续性方程式（5－7）和动量方程式（5－18）并对时间取平均值。为方便起见，除脉动值的时均值外，去掉表示时间值的上划线符号“－”，且引入张量中的指标符号，可得湍流时均流动的控制方程如下：

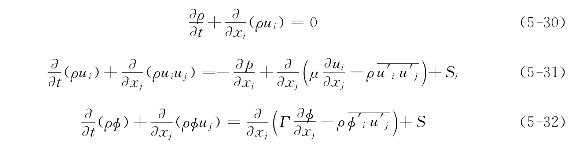
式（5－30）至（5－32）是用张量的指标形式表示的时均连续性方程、动量守恒方程和标量φ的时均输运方程。由于采用的是雷诺平均法，因此式（5－31）被称为雷诺平均纳维－斯托克斯（Reynolds－Averaged　Navier－Stokes，RANS）方程，常直接称为雷诺方程。可以看到，时均流动的方程里多出与有关的项，我们定义该项为雷诺应力，即

这里，τij实际对应6个不同的雷诺应力项，即3个正应力和3个切应力。由式（5－30）至（5－32）所构成的方程组共有5个方程（雷诺方程实际上是3个方程）。现在新增了6个雷诺应力，再加上原来的5个时均未知量（ux，uy，uz，p和φ），总共有10个未知量，因此方程组不封闭，必须引入新的湍流模型（方程）才能使方程组封闭而进行求解。

5.3.3　湍流数值模拟方法

湍流流动是一种高度非线性的复杂流动，但若能通过某些数值方法对湍流进行模拟，可以取得与实际比较吻合的结果。总体而言，目前的湍流数值模拟方法可以分为直接数值模拟（Direct Numerical Simulation，DNS）方法和非直接数值模拟方法。前者直接求解瞬时湍流控制方程，因为方程本身是封闭的，无需引入任何模型假设即可以获取每一瞬间流场中的所有变量，但由于求解需要满足湍流中各种时间和空间尺度，对内存空间及计算速度的要求非常高，现有计算机的能力限制了其应用的普适性。非直接数值模拟方法则不直接计算湍流的脉动特性，而是设法对湍流做某种程度的近似和简化处理，如5.3.2节中介绍的时均性质的雷诺方程就是典型的非直接数值模拟方法。根据所采用的近似与简化方法的不同，非直接数值模拟方法分为雷诺平均法（RANS）、大涡模拟（Large Eddy Simulation，LES）法和统计平均法。前两种方法目前在工程上应用得较为广泛。RANS法将瞬态脉动量通过某种模型在时均化的方程中体现出来，引入雷诺应力的封闭模型求解时均化雷诺方程。雷诺应力的主要贡献来自大尺度脉动，而系统中动量、质量、能量以及其他物理量的输运主要受大尺度涡影响，大尺度涡的性质及结果和流场的边界条件密切相关，因此雷诺应力的封闭模式不可能是普适的。LES法是介于DNS与RANS法之间的数值模拟方法，其核心在于放弃对全尺度涡的瞬时运动进行模拟，只将比网格尺度大的湍流运动通过瞬时N－S方程直接求解，而小尺度涡对大尺度涡运动的影响则通过一定的模型在针对大尺度涡建立的瞬时N－S方程中体现出来，其理论依据是小尺度涡有局部平衡的性质，很可能存在某种普适的统计规律，如：局部各向同性或局部相似性等。本书只对目前在工程上应用最为广泛的雷诺平均法作介绍。

考察雷诺方程（5－31），方程中关于湍流脉动值的雷诺应力项属于新的未知量。要使方程组封闭，必须对雷诺应力作出某种假定，即建立应力的表达式（或引入新的湍流模型方程），通过这些表达式或湍流模型，把湍流的脉动值与时均值等联系起来。由于没有特定的物理定律可以用来建立湍流模型，所以目前的湍流模型只能以大量的实验观察结果为基础。根据对雷诺应力作出的假定或处理方式的不同，目前常用的湍流模型有两大类，即：雷诺应力模型和涡粘模型。雷诺应力模型直接构建表示雷诺应力的方程，然后联系方程式（5－30）至（5－32）进行求解。在涡粘模型方法中，不直接处理雷诺应力项，而是引入湍动粘度（turbulent viscosity），或称涡粘系数（eddy viscosity），然后把湍流应力表示成湍动粘度的函数，整个计算的关键在于确定这种湍动粘度。

湍动粘度的提出源于Boussinesq提出的涡粘假定，该假定建立了雷诺应力相对于平均速度梯度的关系，即

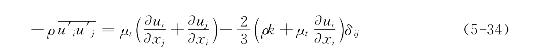
式中，μt为湍动粘度，是空间坐标的函数，取决于流动状态，而不是物性参数；ui为时均速度；δij是克罗内克符号（Kronecker　delta），当i＝j时，δij＝1，当i≠j时，δij＝0；k为湍动能（turbulent kinetic　energy），即

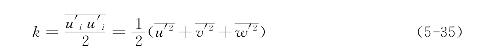
由上可见，引入Boussinesq假定后，计算湍流流动的关键在于如何确定湍动粘度μt。这里所谓的涡粘模型，就是把μt与湍流时均参数联系起来的关系式。依据确定的微分方程数的多少，涡粘模型分为：零方程模型、一方程模型和两方程模型。目前两方程模型在工程中应用得最为广泛，最基本的两方程模型是标准的k－ε模型。

5.3.4　标准k－ε两方程模型

标准的k－ε模型是典型的两方程模型。在关于湍动能k的方程的基础上，再引入一个关于耗散率ε的方程，便形成了k－ε两方程模型，称为标准k－ε模型（standard　k－εmodel）。模型通过建立求解k和ε的方程式，从而对湍动粘度μt进行求解。该模型是由Launder和Spalding于1972年提出的。表示湍动耗散率（turbulent dissipation rate）的ε被定义为

湍动粘度μt可表示成k－ε的函数，即

式中，Cμ为经验常数。

在标准的k－ε模型中，k和ε是两个基本未知量，与之相对应的输运方程为

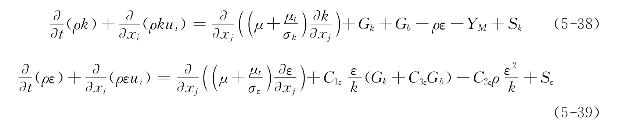
式中，Gk是由于平均速度梯度引起的湍动能k的产生项；Gb是由于浮力引起的湍动能k的产生项；YM代表可压湍流中脉动扩张的贡献；C1ε，C2ε和C3ε为经验常数；σk和σε分别是与湍动能k和耗散率ε对应的普朗特（Prandtl）数；Sk和Sε是用户定义的源项。

5.4　气固两相流数值模拟

5.4.1　气固两相流的模拟方法

工程实际中，经常遇到不同相态或不同组分的物质混合流动、换热以及复杂的化学反应等问题，由于系统多元尺度的复杂性以及受到试验设备、测试系统等方面的限制，试验研究存在很大的困难。而数值模拟方法以其较强的再现能力、低耗费、零危险性等诸多优势，在多相流动与换热体系研究领域发展得很快。目前，广泛应用于颗粒－流体多相流的数值计算方法主要有：欧拉－欧拉方法和欧拉－拉格朗日方法。欧拉－欧拉方法已被广泛地应用于稠密颗粒相的气固或液固流动体系，也称为颗粒相拟流体模型，它把颗粒相处理为具有连续介质特性的、与连续相相互渗透的拟流体，流体连续相和颗粒相都在欧拉坐标系下进行求解，仿造单相流动对颗粒湍流脉动进行模拟，应用颗粒动力学理论以及分子运动论使方程组封闭。颗粒相拟流体模型最大的优点是可以全面地考虑颗粒相的输运特性，能进行大规模的工程问题计算。但该方法中的颗粒连续性假设本身削弱了气固或液固两相流中非均匀结构的真实性，计算中无法体现颗粒的大小、密度等物理性质的区别，模拟结果也无法揭示颗粒复杂的变化经历，如物理、化学特性随时间的变化经历。为此，近年来许多研究者开始尝试采用欧拉－拉格朗日法进行颗粒流的求解。

欧拉－拉格朗日方法将流体相处理为连续相，在欧拉坐标系下建立纳维－斯托克斯方程组求解其流动、传热及反应特性，而在拉格朗日坐标系下应用牛顿第二定律跟踪求解流场中的每一个离散粒子的运动轨迹来反映整个离散颗粒场，连续相－离散相的相互作用服从牛顿第三定律，以源项添加于各自的求解方程中实现相间的作用耦合。由于欧拉－拉格朗日方法直接对离散颗粒的运动轨迹进行求解，模型简化，假设少，并可直接揭示每个颗粒的运动与反应规律，因此与颗粒相拟流体模型相比，该模型要更为合理、精确。但随着颗粒浓度的增加，需跟踪的颗粒数量增多，且颗粒间相互作用也随之变得复杂，计算量会因此受到限制。不过随着目前高性能计算机计算能力的飞速发展，欧拉－拉格朗日法对于颗粒多相流体系的研究应用越来越广泛。

5.4.2　气固两相流的基本方程以及相间的耦合

5.4.2.1　连续相流动控制方程

气固两相流区别于单相流最基本的特征是连续相空隙率（αf）的引入。连续相空隙率表示的是控制体中气体所占的体积份额，即

式中，Vk，p是控制体中第k相颗粒的总体积，V是控制体的体积。

由于参数αf的引入，需要对单相流的基本守恒方程作相应的修改，从而描述气固两相流中连续气体相的方程。气固两相流中气相连续性方程为

动量守恒方程为

式中，Fsf是离散颗粒相对流体的作用力，将在5.4.2.2节中关于离散相控制方程的部分进行介绍。在许多工程问题中，气体的流动呈紊乱的湍流态，如鼓泡床、喷动流化床等。在这些情形下，相应的气固两相流模式下的标准k－ε模型方程为

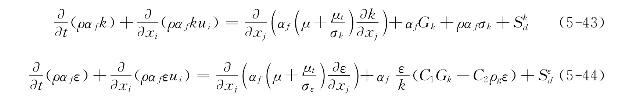
式中是由于颗粒的运动引起的湍动能k的产生项，定义为

这里，β是流体曳力系数。式（5－45）右边的第一项是由于固体颗粒阻碍而引起的k产生项，第二项是气固两相间湍动能交换项，也称为湍动能重分配项。Δu是气相速度波动，Δv是颗粒相速度波动。湍动能重分配项可以计算为

式中，τd是颗粒相相应时间尺度，τl是气体相拉格朗日时间尺度，定义为

这里，σs是湍动施密特（Schmidt）数。

而式（5－44）中，则是由于颗粒相而引起的耗散率产生项，可计算为

式中，C3是经验常数。不同情形下，这些经验常数的值可参照相关书籍和文献。

5.4.2.2　离散相控制方程

欧拉－拉格朗日方法中对固体相的每个颗粒单独进行求解，从而获得详细的颗粒运动动力学信息，包括颗粒－颗粒、颗粒－流体以及颗粒－器壁间相互作用。根据牛顿第二定律，颗粒相的运动求解方程为

式中，mp，Ip分别为颗粒的质量和惯性项；Ffp是连续气体相作用于颗粒的流体力，Ffp＝－Fpf；Mfp是作用于颗粒上总的旋转矩。作用于颗粒上的主要流体力随不同的工程应用背景而发生变化。一般而言，可能存在几种重要力，主要包括：流体曳力（drag　force）、马格努斯旋转提升力、萨夫曼剪切提升力、倍瑟特力、压力梯度力、虚拟质量力。本书中第4章对这些力做了详细的介绍。

5.4.2.3　相间的耦合

气固相间的耦合主要包括动量和能量间的耦合，本文只对冷态下的气固两相流模拟进行讨论，故仅介绍动量间的耦合。动量间的耦合主要通过相间的作用与反作用力实现，遵循牛顿第三定律。气固相间的耦合是气固两相流数值模拟中最关键的部分，它直接决定着模拟结果的准确性。随着欧拉－拉格朗日方法的广泛应用，对气固相间耦合的研究越来越多，有大量文献和研究报导可供读者参阅.