二元离散型随机变量

定义3.1.1　若二元随机变量（X，Y）的取值有限或可列，则称（X，Y）为二元离散型随机变量或称二元离散量。

（一）二元离散量的联合分布

设二元离散量（X，Y）的可能取值为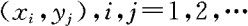，与一元离散量相似，称

为（X，Y）的联合概率分布律或简称联合分布律。上式亦可用列表的方式表示。

联合分布律满足。

由概率的性质知（1）成立，又是样本点，所以两两不相容，且其全体构成一样本空间，故（2）亦成立。

例3.1.1　一袋中有5个白球，1个红球和2个黑球。每次摸1球，不放回抽样3次。设3次中有X次摸到白球，Y次摸到红球，求（X，Y）的联合概率分布律。

解　由题意知，X的可能取值为0，1，2，3，Y的可能取值为0，1。记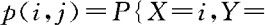，则（下式中即为组合数）

（二）二元离散量的边际分布

设二元离散量（X，Y）的联合分布律为 ，故有

同样可得

注：符号“”表示“记为”。

显然有，，即（3.1.2）及（3.1.3）满足分布律的性质，它们分别是随机变量X与Y的概率分布律，分别称为关于X及关于Y的边际分布律或边缘分布律。用列表的方法来表示联合及边际分布更能理解其字面的意义。

上表内第i行（或第j列）累计后记作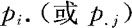，上表列在联合分布律表的边上的这一列（或一行）恰是X（或Y）的分布律，故称其为边际分布律。

例3.1.2　设一群体80％人不吸烟，有15％的人少量吸烟，5％的人吸烟较多，且已知近期他们患呼吸道疾病（以下简称患病）的概率分别为5％，25％，70％。记

求：（1）（X，Y）的联合分布与边际分布；（2）求患病人中吸烟的概率。

解　（1）记。由题意知，X的边际分布律为

（2）要求的概率为

即患病的人中有近65％的人吸烟。

（三）二元离散量的条件分布

从上面的例3.1.2（2）可以看到，研究二元离散量的条件概率是有趣和必要的。下面我们就来研究一下二元离散量的条件分布问题。

设二元离散量（X，Y）的联合分布律为，

则当时，

同理可得，当时，

称（3.1.4）（或（3.1.5））式为给定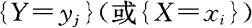的条件下X（或Y）的条件分布律。

（3.1.4）式中显然有。同样，（3.1.5）式中有。亦即（3.1.4）及（3.1.5）式满足分布律的性质。

例3.1.3　设二元离散量（X，Y）的联合概率分布律为

且已知求：（1）a，b的值；（2）｛X＝2｝的条件下Y的条件分布律；（3）｛X＋Y＝2｝的条件下X的条件分布律。

解　（1）。由联合分布律的性质知，a＋b＋0.6＝1，得b＝0.4。

（2）P｛X＝2｝＝0.1＋0.1＋b＝0.6。那么｛X＝2｝的条件下Y的条件分布律为

也可以写为

（3）P｛X＋Y＝2｝＝P｛X＝2，Y＝0｝＋P｛X＝1，Y＝1｝＝0.3，那么

例3.1.4　设一单位送客车上车人数X服从参数为λ的泊松分布，每个人行动独立，每个上车人在中途下车（没有坐到终点站）的概率为p，0＜p＜1，设中途只下不上，并记中途下车的人数为Y。求（X，Y）的联合分布律，X与Y的边际分布律以及条件分布律。

解　已知。且由题意知，当m＝0，1，2，…时，

即。

例3.1.5　一种叫“排列3”的彩票：每次从0～9这10个数中随机取一个数，共取3次，得3个数的一个排列作为一期彩票的大奖号码。王先生每一期去买10个不同排列的号码。设X为他首次中大奖时已买的彩票期数，Y表示第2次中大奖已买彩票的期数。（1）求（X，Y）的联合分布律；（2）已知他买了100期时第2次中大奖，求X的条件分布律。

解　（1）由题意知，每一个号码中大奖的概率为1/103。买10个不同号码，中大奖的概率为1/100。记p＝1/100。

设Ai＝｛王先生买了第i期彩票中大奖｝，i＝1，2，…则

即当已知王先生在买了100期彩票时第2次中大奖，则第1次中大奖在前99期中是等可能的。