变量消元算法

14.4.2 变量消元算法

通过消除类似图14.8中所示的那种重复计算能够大大提高枚举算法的效率。其思想非常简单：只进行一次计算，并保存计算结果以备将来使用。这是动态规划的一种形式。这种方法有几种不同的版本；这里我们给出其中最简单的变量消元算法（variable elimination algorithm）。变量消元算法的工作方式是按照从右到左的次序计算诸如公式（14.3）的表达式（也就是按照图14.8中自底向上的次序）。中间结果被保存下来，而对每个变量的求和只需要对依赖于这些变量的表达式部分进行就可以了。

让我们以防盗网络为例描述这个过程。我们计算表达式

注意到我们已经用相关变量名标出了表达式的每个部分，这些部分称为因子（factor）。具体步骤如下：

• M的因子P(m|a)不要求对M进行求和（因为M的取值已经确定）。我们用一个二元向量来保存每个给定的a值下的概率：

（其中fM表示通过M生成f。）

• 类似地，我们将J的因子存储为一个二元向量fJ(A)。

• A的因子是P(a|B, e)，它将是一个2 × 2 × 2 矩阵fA(A, B, E)。

• 现在我们必须通过求和运算将A从这3个因子的乘积中消去。这样我们将得到了一个只有B和E的2 × 2矩阵。我们在矩阵名字A上面加一横表示它已经通过求和被消去了：

这里所使用的乘法过程称为点积（pointwise product），后面会简要地介绍它。

• 我们用同样的方式处理E：在fE(E)和(B,E)的乘积中对E进行求和消元：

• 现在我们可以简单地将B的因子（即f(B)=P(B)）与累积矩阵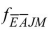相乘来计算答案：B

习题14.7（a）要求你检验这个过程能得到正确的答案。

检查这个步骤序列，我们发现需要两种基本的计算操作：计算两个因子的点积，以及在因子乘积中对一个变量求和消元。

上面的点积既不是矩阵乘法，也不是因子中逐个元素相乘。点积是由两个因子f1和f2得到一个新的因子f，其变量集是因子f1和f2变量集的并集。假设这两个因子有公共变量Y1,…,Yk，那么我们有

f(X1,…,Xj,Y1,…,Yk,Z1,…,Zl)=f1(X1,…Xj,Y1,…,Yk)f2(Y1,…,Yk,Z1,…,Zl)

如果所有的变量都是二值的，那么f1和f2各有2j+k和2k+l个元素，它们的点积有2j+k+l个元素。例如，给定两个因子f1(A, B)和f2(B, C)的概率分布如下表所示，则点积f1× f2表示为f3(A, B, C)：

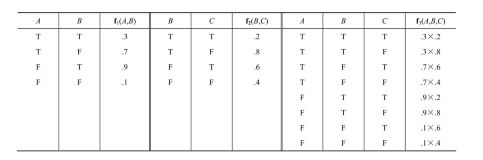
从因子乘积中对一个变量进行求和消元也是非常直接的计算。唯一需要注意的技巧是，任何不依赖于将被求和消元的变量都可以移到求和符号的外面。例如，

现在计算求和号内层的点积，并将变量从结果矩阵中求和消去：

注意直到我们需要将变量从累积乘积中消去之前不会进行矩阵乘法。因此，我们只对包含被求和消元的变量的矩阵进行相乘运算。给定了点积以及求和消元的例行程序后，变量消元算法本身可以非常容易地写出来，如图14.10所示。

让我们再考虑另一个查询：P(JohnCalls|Burglary = true)。照常，第一步是写出嵌套的求和式：

如果我们从右向左对这个表达式进行求值运算，我们就会发现一件非常有趣的事情：根据定义有∑m P(m|a)等于 1，因此，一开始就没必要包括它；变量 M 和这个查询无关。另一种说法是，即使我们把节点MaryCalls从网络中删除，查询P(JohnCalls|Burglary = true)的结果也不会发生变化。总的来说，我们可以删除任何既非查询变量，也非证据变量的叶节点。在这样的删除之后，可能会生成一些新的叶节点，它们与查询变量仍然无关。继续这个过程，我们最终发现，所有既非查询变量亦非证据变量的祖先的节点都和查询无关。因此在变量消元算法中可以在对查询求值之前删除所有这些变量。

图14.10 回答贝叶斯网络上的查询的变量消元算法