基于测耦检波器的野外耦合响应规模测量与衰减

从实际应用的角度来看，“测耦检波器”主要有两个方面的用途。

1.实时监测、量化记录每个检波器的耦合状况

图2-21为耦合状况实时监测画面（左图）以及绘制出来的响应的耦合响应曲线（中图）。在野外施工时，存在高山密林、大漠戈壁、山高水深等各种情况（图2-21右图），监控难度大。同时，挖坑埋置后，人们无法直观地看到埋置状况，更不用说量化评价。而借助测耦检波器，我们可以看到每个检波器（单点）的耦合状况，对耦合差的检波点进行改正，对耦合好的检波点进行记录，以便为今后进行耦合响应校正提供参数。因为测耦检波器可以独立测量耦合响应，不需人工干预，这就大大提高了检波器埋置质量的监控效率。无论对于监督力量无法覆盖的密林、沼泽、绝壁等复杂地表，还是经过挖坑埋置、水中埋置后只能少量抽检的情况，都可以实现检波器埋置状况的实时检测，对于提高施工效率与质量，均会有很大推动作用。

图2-21　测耦检波器可以实现对每个检波点（单点）耦合情况的监控与记录

同时，在测得每个单点检波器耦合响应的情况下，不需要将每个检波器挖深坑埋置。因为挖深坑埋置的主要目的是改善耦合介质的弹性参数（密度、泊松比、速度等），进而提高耦合效果，即将耦合曲线的高频段尽量“下压”（图2-22）；而在采用测耦检波器的情况下，只要将检波器埋置于均匀土壤介质中，紧密、垂直与土壤接触（减小检波器-大地耦合系统的非线性）并用土覆盖表面（减少风的干扰）即可。此后根据测得的耦合参数，即可以基本消除耦合响应，而挖坑埋置的作用仅仅是降低耦合响应。类似地，不同检波器由于其外形、材质、质量的不同，也具有不同的耦合响应，图2-19展示了动圈式20dx检波器（埋置全部尾锥）与ME MS数字检波器DSU3（埋置全部外壳）的比较。由图2-19可见，DSU3数字检波器因为自身质量、材质等因素，耦合效果较差（高频响应更强）。该检波器的这一特性在一定程度上抹杀了它作为加速度检波器、在高频段具有较高机电信噪比的优势。

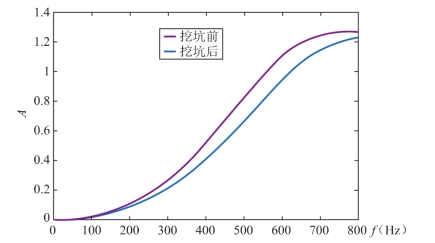
图2-22　挖坑埋置前后耦合响应的变化

2.根据野外记录参数消除耦合响应——耦合反褶积

鉴于耦合响应对地震数据的影响，有必要通过一定的方法，还原地震数据受耦合响应影响之前的本来面貌，提高地震数据刻画地质现象的精细度。

实现消除检波器-大地响应的途径之一是采用耦合反褶积。此前，因为没有实际测量到准确的耦合脉冲响应，这种设想是不可能实现的。在测耦检波器的基础上，可以将这一设想变为现实。

反滤波器（反褶积）是使其脉冲响应与信号褶积时，能消除某些前面加到信号上的滤波作用。例如，地震波在地层内传播，可以将地层看成是具有某种性质的滤波器。因此，可以通过反褶积将这些滤波作用去掉，近似地恢复激发信号的形状，以提高分辨能力。耦合响应也可以被视为一种对地震波的滤波效应，所以在已知其脉冲响应的前提下，可以对数据进行“反滤波”，以消除耦合响应的影响，提高数据保真度。［36］

（1）最小平方反滤波（LSD）求反算子。

由于耦合的频率响应函数可能存在零点，如果直接取其倒数，会出现无穷大值点，造成相应的时间域滤波因子剧烈震荡，进而导致滤波结果无法辨认。因此，考虑用最小平方反滤波的办法求取其近似的时间域反滤波因子，再对地震记录进行滤波。

①快速傅里叶变换（FFT）。

已知耦合频率响应函数H（f），求其时间域滤波因子h（t）需要用反快速傅里叶变换IFFT方法。

傅里叶变换是建立以时间为自变量的信号和以频率为自变量的频谱函数之间的某种对应关系。因为计算量太大，用离散傅里叶变换（DFT）进行谱分析是不切实际的。20世纪60年代中期，人们首次发现了DFT的快速算法，经过不断发展与完善形成了快速傅里叶算法（FFT），它的运算速度可比DFT提高1～2个数量级。

计算n个采样点H（t）＝｛H0，H1，…，Hn-1｝的离散傅里叶变换，可以归结为计算多项式h（x）＝H0＋Hlx＋…＋Hn-1Xn-1在各n次单位根1，ω2，…，ωn-1的值，即

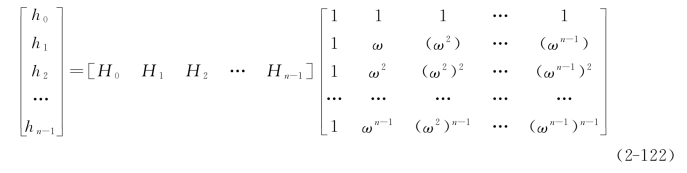
其中，ω＝e2πj/n（j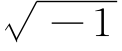＝）为n次单位元根。

若n是2的k次幂，即n＝2k（k＞0），则h（t）可以分解为关于x的偶次幂与奇次幂两部分，即

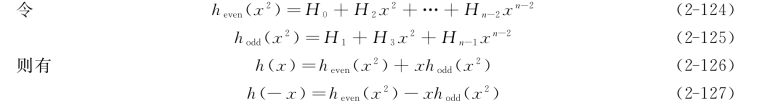
可见，为求h在各n次单位根上的值，只要求heven和hodd在1，ω，ω2，…［ω（n/2）-1］2上的值即可。而heven和hodd同样可以分解成关于x的偶次幂与奇次幂两部分，依此类推，一直分解下去，最后只要求二次单位根1和-1上的值。实际计算中，可将上述过程倒过来进行，这就是快速傅里叶变换。

编程时调用响应函数的实部FR［h（f）］用和虚部FI［h（f）］用作为输入。二者均为长度为N的双精度实型一维数组，相当于上述计算中的偶次幂与奇次幂两部分，返回时分别输出逆傅里叶变换即h（t）的模和辐角（均为长度为N的一维数组）。为简便，采用其模作为h（t）的离散值。

②最小平方反滤波。

最小平方滤波（褶积）是一种最佳滤波，即按照最小平方准则来设计滤放器（图2-23）。这种方法具有简单、灵活、高效的特点，因此在信号数字处理中，最小平方滤波已成为基本滤波方法之一。最小平方反滤波是最小平方滤波（或称最小二乘法）的一种特例，即针对某个滤波器按照最小平方准则设计其反滤波因子，用这个反滤波因子与滤波后的地震记录相褶积，以消除该滤波器的影响。这相当于滤波的反过程，因此称为反滤波。

图2-23　最小平放反滤波

a.反滤波的基本概念。

所谓反滤波，仍然是一个滤波过程，但它恰好与其他某个滤波过程的作用相反。

设x（t）是时间函数h（t）的滤波器的输入，y（t）为输出，则有

现在要设计一个滤波器，使得当y（t）作为输入时，输出是x（t），即

则a（t）是h（t）的反滤波。

综上，可以得到

根据δ函数理论，有

上式即滤波因子h（t）与反滤波因子a（t）之间的关系。在频率域中，二者对应的傅里叶变换A（f）、H（f）之间的关系是A（f）·H（f）＝1，

用Z变换形式表示

该式是一个有理分式的Z变换，H（Z）为一个多项式。显然A（Z）＝1/H（Z）一般是一个无穷级数，a（t）是一个无穷序列。

b.最小平方反滤波的基本原理。

最小平方滤波的思想在于设计一个滤波算子，用它把已知的输入信号转换为与给定的期望输出信号在最小平方误差的意义下为最佳接近的输出信号。

设输入信号为x（t），使它与待求的滤波因子h（t）褶积得到实际输出y（t）＝x（t）＊h（t）。设期望输出为y（t），用最小平方误差准则判断实际输出与期望输出是否最佳接近，当两者的误差平方和最小时，求出滤波因子h（t）。此时，用h（t）对输入信号进行滤波，称最小平方滤波。

若再设计一个滤波器，x（t）是该滤波器的输出，而期望输出y（t）是该滤波器的输入，按此思路求得的滤波因子a（t）即为最小平方反滤波因子，用它进行的滤波是最小平方反滤波。

最小平方反滤波是将记录中的地震子波压缩成尖脉冲，是提高垂向分辨率的方法。

设地震子波为b（t），反射系数序列为R（t），则地震记录x（t）为

现在要设计一个反滤波器a（t），a（t）＝［a（0），a（1），…a（m）］使地震子波b（t）变成窄脉冲，

地震记录x（t）经反滤波器a（t）作用后的实际输出为

期望输出的是一系列窄脉冲，

根据最小平方反滤波的思想，信号经反滤波作用后的输出应是c（t）与z（t）在最小平方误差时的最佳输出。

c.最小平方反滤波数学模型。

输入信号（滤波因子）h（t）＝［h（0），h（1），…，h（n）］

反滤波因子g（t）＝［g（-m0），g（-m0＋1），…，g（-m0＋m）］

期望输出（δ脉冲）（t）＝［1，0，…，0］

误差能量

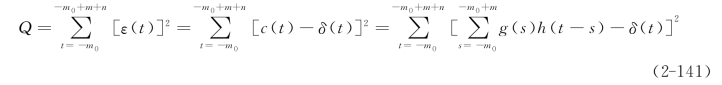
要使误差能量最小，数学上就是求Q的极值问题，即求满足

的滤波因子g（t）。

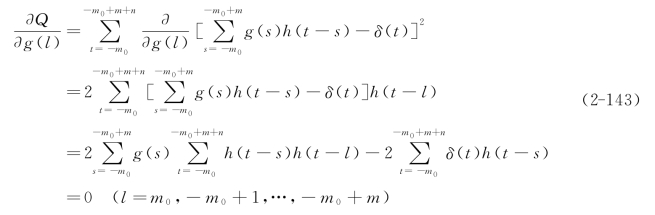
因为为滤波因子的自相关函数，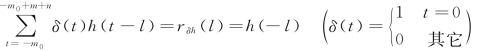

而为滤波因子与期望输出的互相关函数，故（2-143）式可写为

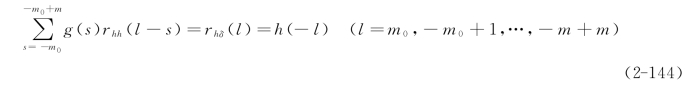
该式是一个方程组，写成矩阵形式如下

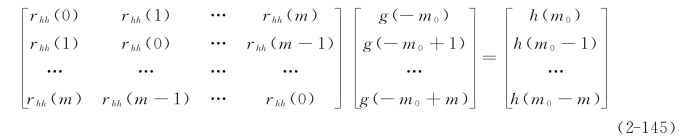
该方程组的系数矩阵即托布利兹矩阵，是一种特殊的正定矩阵，它不但以主对角线为对称，也以次对角线对称，且主对角线及与主对角线平行的直线上的元素均相同。（2-145）式是最小平方反滤波的基本方程，可用专门的莱文森递推法求解。

由方程组可知，只要知道耦合的传递函数h（t），求出其自相关函数rhh（l）（l＝0，1，2，…，m），代入该方程组求得反滤波因子g（t），用它与地震记录褶积，即可消除耦合效应。

即反滤波结果接近真实的地面振动。

d.提高垂直分辨率与提高信噪比的关系。

一般来说，反滤波在提高垂直分辨率的同时会降低信噪比。脉冲反滤波不能区分信号和噪声，只能考虑总的振幅谱。理想反滤波的输出是白噪反射系数序列，从频率上说，就是将地震记录的谱变为幅值近似相等的白噪声谱。这样，如果记录的干扰没有消除干净，则残留的干扰会同时得到放大。即经反滤波后噪声的高、低频成分表现出较大的振幅，脉冲反滤波的输出常常出现噪声或尖峰，于是降低了信噪比。因此，在进行反滤波之前，应当最大限度地压制干扰，在反滤波之后还需进行宽带滤波，以提高信噪比。

e.有限长物理可实现信号的反信号。

对于任一信号h（n），如果信号g（n）满足h（n）＊g（n）＝δ（n）（脉冲信号），则称g（n）是h（n）的反信号，或称h（n）的反滤波因子。有关m＋1项物理可实现信号的反信号的特点如下。

m＋1项信号h（n）＝h（h0，h1，…，hm）。设h（n）的反滤波因子g（n）的Z变换为G（z），则有

这里讨论混合延迟的情况。

当h（n）为混合延迟，且所有根｜aj｜都满足｜aj｜≠1（即不在单位圆上）时，可把aj分为两组，一组为，j＝1，2，…，m1，满足｜｜＞1，一组为，j＝1，2，…，m2，满足｜｜＜1，其中（m1＋m2＝m），这时

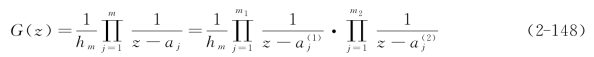
并且

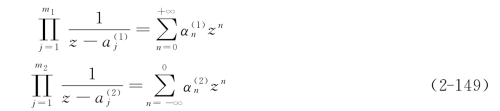
因此，G（z）可表示为

这表明反信号g（n）在时间的正负两个方向上皆有值。

另一种情况，当h（n）为混合延迟，且至少有一根a，使｜a1｜＝1，这时至少有一f0，使

因此所以，不存在这样的G（f）使得H（f）G（f）＝1对每一点f都成立。这样的反滤波频谱不存在，因此可认为反滤波因子即反信号g（n）也不存在。

f.托布利兹（Toeplitz）方程的递推解法。

托布利兹方程（2-145）是一种特殊形式的线性方程组，其形式为

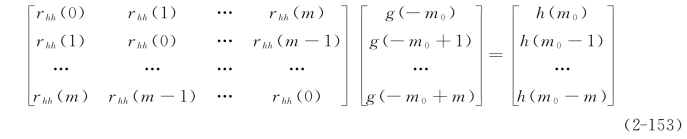
在该式中，rhh（j）、h（j）都是已知的，g（j）是未知的。

为简化起见，把rhh（0），rhh（1），…，rhh（m）依次记为r1，r2，…，rm＋l；把g（-m0），g（-m0＋1），…，g（-m0＋m）依次记为x1，x2，…，xm＋1；把h（m0），h（m0-l），…，h（m0-m）依次记为h1，h2，…，hm＋1；则上述方程组可写为

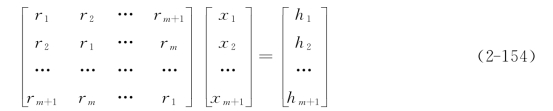
形如上式的方程，称为托布利兹方程，方程的系数矩阵

称为托布利兹矩阵。

在最小平方滤波中都要遇到解托布利兹方程的问题，由于托布利兹方程是一种特殊形式的线性方程组，所以托布利兹矩阵有一种特殊解法，即递推解法。它的基本思想：m阶方程组的解可以用m-1阶方程组的解表示，m-1阶方程组的解可以用m-2阶方程组的解表示。这样，只要知道一阶方程组的解，就可以一步一步递推出任意阶方程组的解。

③最小平方反滤波过程中的几个关键问题。

在用最小平方法解托布利兹方程求反耦合滤波因子过程中，会遇到诸如预白噪、参数m 与m0的选择、能量保持处理等几个关键问题，这几个问题能否解决得好关系到反滤波结果的优劣，因此下面分别详细介绍。

a.预白噪问题。

直接求解（2-145）式效果往往不好，具体分析原因如下：当-m0→-∞，-m0＋m→＋∞时，（2-145）式变为

即

对应于频率域，上面关系为

其中，Rhh＝｜H（f）｜2。当｜H（f）｜有零点或接近于零点的时候，G（f）就不存在或取值非常大，反映在时间域反滤波因子g（t）收敛缓慢，震荡激烈，反滤波效果不好。

解决上述问题的办法是预白噪化。

把2-145式中的系数矩阵rhh（n）做如下变换：

λrhh（0）δ（n）的频谱等于λrhh（0），为一常数，由于白光的光谱是均匀分布的，实际中许多噪声信号的谱也近似于常数，因此把λrhh（0）δ（n）称为白噪相关函数，把加白噪的过程叫做预白噪化。λ通常是一个很小的正数，叫作白噪系数，可根据记录中噪声水平人为调节，一般取在0～0.2之间。

然而，白噪化后反滤波的结果会在尖脉冲（极大压缩后的组合滤波因子）后面跟上一个小的摆动。小摆动的出现又会降低反滤波结果的分辨率，λ越大，影响越大。因此要取一个适当的λ值，既使反滤波因子g（t）稳定，又使Q＝∑［g（t）＊h（t）-δ（t）］2的值较小，跟在后面的小摆动就会衰减的快些。取λ时，要根据信号h（t）的振幅谱的特点来确定。原则上是｜H（f）｜越接近于零，λ就越取的稍大些。另外，也可通过取不同的λ值进行试验，以确定合适的值。由于g（t）稳定，就可以取有限长度因子［g（-m0），g（-m0＋1），…，g（-m0＋m）］很好地近似g（t）。因此，经过白噪化后再解方程组（2-145），就可以得到较好的反滤波因子和较好的滤波效果。

b.参数m与m0的选择问题。

解（2-145）式时会遇到m与m0的选择问题，这两个参数选择是否合适直接影响到反滤波的效果。选择参数的方法会因滤波因子是最小相位信号还是混合相位信号而不同。检验信号是最小相位还是混合相位的一个简便办法是看其波形的能量主要聚集的位置。如果能量主要聚集在信号前端，则该信号是最小相位延迟信号，简称最小相位信号；如果能量主要聚集在信号中间，则该信号是混合相位延迟信号，简称混合相位信号。

针对混合相位信号，确定参数m与m0的方法如下。此时，严格的反滤波因子g（t）在整个时间轴（-∞，＋∞）上都有值，因此在选取最小平方反滤波因子g（t）的时候，一般取m0＞0，-m0＋m＞0。

实际应用中可采取试验的方法确定m与m0。第一步，找出混合相位信号h（t）最大振幅值所在的时间t0。第二步，取-＝-to-l，-＋＝-to＋l，其中l是一个比较大的正数。对这样的与，解方程得到反滤波因子g（t）＝（g-），g（-＋1），…，g（-＋）。第三步，根据g（t）的波形，把两端振幅值较小的部分截掉，使g（t）的能量主要集中在（-m0，-m0＋m）之上。其中，-＜-m0，-m0＋m＜-＋。然后根据现在的m和m0，再解方程（2-145），即可得到g（t）。这就是要求的实际应用的反滤波因子。

以上所述实际上是当h（t）为不同相位信号时，最小平方反滤波因子g（t）中m0的选取原则。最小平方反滤波因子g（t）的长度为m＋1，m的取值范围比较广，可在30～200之间。对反滤波的要求较高时，可取m在100～200之间；要求不高时，可取m在30～60之间。

c.能量保持处理。

反滤波的目的是将拉伸的信号压缩为一个尖脉冲，而这个尖脉冲既能反映原来信号的变化方向，又能保持原来信号的能量水平。因此，需要对反滤波因子进行能量保持处理，即将白噪化处理后的反滤波因子g（t）乘上一个系数。

解方程（2-89）可得h（t）的反滤波因子g（t），h（t）经过g（t）滤波后变为

上式右边不能反映h（t）的运动方向，为了刻画h（t）向上或向下运动的特点，我们选择一点t0，使h（t0）的符号能反映h（t）向上或向下的特点，例如可取h（t0），使｜h（t0）｜为｜h（t）｜的最大值。h（t0）的符号为

把反滤波因子g（t）变为g＾（t）

其中

用g＾（t）对h（t）进行滤波，就是所谓的保持能量不变、方向不变的最小平方反滤波。［36］

（2）具体做法与实际效果。

在进行“耦合反褶积”，即由检波器输出数据求取地面震动数据的时候，需要注意公式转换的问题。因为我们利用公式

进行振动参数模态识别的时候，其输入信号的傅里叶变换式为

并且激励力信号是施加于检波器上、相当于振动系统中质量块m上的。在实际的地震波接收时，地震波是由地面传导到检波器上，即相当于由振动系统的支座传播到质量块m上，适用公式可导出

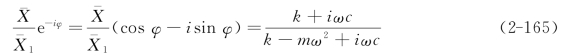
所以，输入检波器-大地耦合系统的大地振动位移信号与检波器振动位移信号之间的关系也可以用公式2-165表达。同时因为

所以，大地振动速度与检波器输出速度信号（不考虑检波器自身的滤波效应）之间的频域关系，也可以用公式（2-165）表示。也就是说，在通过检波器输出速度信号求取大地振动速度信号的时候，适用于公式（2-165），而不是通过参数扫描、求取振动模态参数时所用的公式（2-163）。

在以上分析的基础上，利用我们发明的专利装置，测得每个检波器的耦合响应（图2-24）后，即可以利用反褶积或者反滤波的方法，将该检波器接收到的数据进行耦合反褶积，消除耦合响应的影响，提高信号的保真度（图2-25）。

由图2-24可见，耦合响应会对大地振动（地震检波系统的输入信号）产生一种高频放大作用。实验表明，在多数情况下，耦合谐振频率多高于200Hz，频率越低，畸变越大。

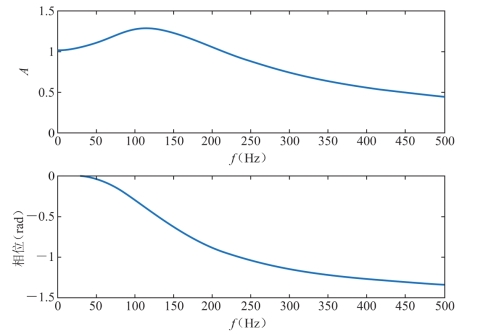
图2-24　检波器-大地耦合频率响应

图2-25　原始数据与经过检波器反褶积以及再进行耦合反褶积之后的波形与频谱

由图2-25可以看出，在低频段，检波器响应（特指存在低频滤波效应的动圈式检波器）在起作用，可以通过检波器反褶积进行低频补偿（详见第三章第三节）。但是，因为地面震动信号中既有低频反射信号，也有低频噪音，比如次生噪音、面波、环境干扰等等，所以，利用检波器反褶积进行“低频补偿”后，需要根据恢复信号的特征，进行针对性的去噪，提高低频端的信噪比（因为爆炸信号是低频丰富的）。而对于高频的耦合响应而言，通过耦合反褶积消除的，是一种“多出来”的信号，是一种纯噪声，并且主要在高频段，特别是100～200Hz起作用。因为低于100Hz，多数耦合响应畸变不大；高于200Hz，震源激发存在一定困难，特别是激发出超过环境高频的有效信号。另由图2-25可见，超过300Hz至高截频率之前，因为地震检波系统输入的反射信号比较弱（高频吸收），环境噪声中高频也比较弱，使得电噪声相对变强。此时，通过“耦合反褶积”放大的，主要是电噪声，产生了很大的失真，是不可信的。

对于“检波器反褶积”补偿的低频信号以及由耦合反褶积衰减的高频噪声来说，其作用都是使得地震数据在更大程度上代表了地面震动，即提高了信号的保真度。因为相较于检波器数据而言，大地振动的保真度是100%。

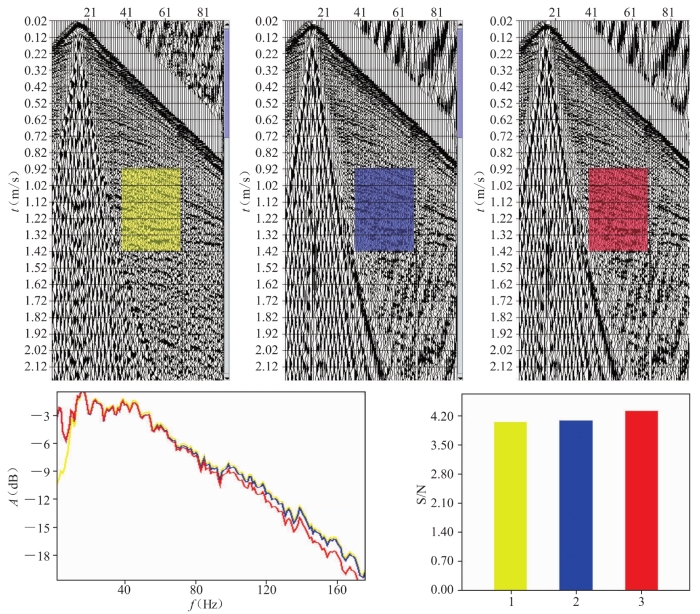
图2-26　在原始数据（黄）基础上进行检波器反褶积（蓝）、再进行耦合反褶积得到的地震记录（红）

需要说明的是，以往多数地震数据都是基于动圈式检波器的速度数据，没有进行以上两类反褶积。在进行二类校正后，数据呈现了不同的高低频特征，所以在数据处理以及地质解释方面的更多应用需要进行进一步的深入研究，特别是低频信号对于波形反演、速度分析、深层成像，低频阴影分析等方面，耦合反褶积后高频信号对于提高高频弱信号的信噪比、保真度、同相性以及分辨率，识别微小地质体的能力等方面。