常用统计量

一、常用统计量

在描述一个变量的取值情况时，常用到“分布”这个词，这个概念应该并不陌生。它主要是反映变量取值的变化情况以及取每个值的样本个数等信息。例如，在一项媒介调查中，得到了表3—1的统计结果。

表3—1　　　被访者收看电视的主要目的（多选，不限选项）

注：此调查结果来自一个配额抽样样本，被访者都是年龄在18～42岁的北京城区白领观众。

表3—1就反映了被访者所作选项的分布情况。例如，从该表中可以看出，被访者看电视的最主要目的是“了解时事”，因为它所占的比例最多（68.3%）；其次是“娱乐消遣”，等等。

在描述变量的分布时，离不开统计量。所谓统计量，是描述样本情况的一些数字，它们是根据样本的取值计算出来的。表3—1中已经出现了两种统计量：频数和比例。

下面我们就介绍一些常用的统计量。

（一）频数和比例

在整理一组资料时，通常最先做的事情之一就是统计某变量的每一个值出现了多少次。这就是频数。频数常用f表示，它是指样本中对某变量具有相同的变量值的个案数。通常把该变量的每一个取值以及取各个值的频数列成一张表格，叫频数表。表3—1就是一张频数表。

在很多时候，比例（百分比或比率）通常比频数更有表现力，因为比例还反映了和样本量有关的信息。比如我们听到“有273人看电视的主要目的是了解时事”的说法，就不如听到“有68.3%的人看电视的主要目的是了解时事”这一说法更好。因此在频数表中，常常同时列出频数和比例两个统计量，甚至有很多频数表只列出比例而不列出频数。比例的计算方法是：

比例P＝f/n×100%

式中，f表示某一频数，n表示样本量或某一类别的子样本数。

频数虽然简单，但它却能直接地反映某一现象的数量多少。不同的频数不仅对某一现象的特征及其规律提供了一个最基本、最初步的定量认识，而且也为深入分析和研究这一现象复杂的数量关系提供了比较和计算的依据。

（二）均值、中位数和众数

这三个统计量都是用来描述分布的中心，即揭示变量取值的集中趋势。

1.均值（Mean）

均值是最普遍使用的中心趋势度量。计算变量X的一组观测值X₁，X₂，…，X_n的平均数，只要把每个样本的取值全部加起来，再除以样本的个数n即可。用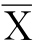表示平均数，则有：

式中的符号∑表示将所有的X_i（i＝1，2，…，n）累加的意思。注意，只有当变量X是定距变量或定比变量时，计算均值才有意义；如果变量是定序或定类变量，则需要用中位数或众数表现其中心趋势。

2.中位数（Median）

中位数是描述定序变量分布中心趋势的一种典型的度量，不过有时也用它来表示定距变量或定比变量的中心。中位数是“最中间的数”，也就是说，要找到一个数，使得有一半的观测值比它小，一半比它大。这个数就是中位数，用M表示。寻找中位数的步骤如下：

（1）将所有n个样本观测值按由小到大的顺序排列。

（2）如果观测值的个数为奇数，中位数M就是排序后最中间的观测值。要找到中位数的位置，只要从头数起，数到第（n＋1）/2个位置即可。

（3）如果观测值的个数为偶数，中位数M就是排序后最中间的两个观测值的平均。要找到这两个数的位置，也是从头数起，数到第n/2个和第（n/2）＋1个位置即可。

例如，假设下列一组数据是一个定序变量的取值：

18、25、16、12、37、23、28、15

其中位数的计算过程：①首先将这8个数从小到大排序为：12、15、16、18、23、25、28、37。②因为观测值的个数是偶数8，中间位置的第4个和第5个数分别是18和23，因此中位数是M＝（18＋23）/2＝20.5，8个观测值中各有4个分别小于和大于这个数。

中位数不适合于定类变量，因为中位数的定义依赖于数据的大小顺序。

3.众数（Mode）

众数常用来表示定类变量的一组取值中出现次数最多的值，这个值也可能是用文字表示的类别或代码，有时其他度量尺度的变量也用众数去表示。众数只是记录发生最频繁的值，这个值可能离分布的平均数或中位数很远；众数也可能不止一个。众数很容易求得，一般一组取值中频数或比例最大的取值就是众数。例如，在表3—1中，可以很快看出，收看电视主要目的的众数就是“1.了解时事”。

（三）极差、四分位数差、方差和标准差

这几个统计量是描述变量分布的离散趋势的，即反映数据的散布情况的。它们常常和均值、中位数、众数配合使用，共同对变量的分布进行描述。

1.极差（Range）

描述分布离散程度的最简单方法就是找出样本观测值的最大值和最小值，这两个数表示了数据的分布范围，称它们的差为极差。即：

极差R＝最大值-最小值

虽然极差一般情况下可以反映数据的分布范围，但是没有给出关于分布中间部分如何变化的任何信息；而且最大值和最小值也有可能是远离其他观测值的特殊值，不能反映大部分数据的分布范围。因此极差是不可靠的，一般不常用。

2.四分位数差（Inter-Quartile Range）

将全部样本观测值按从小到大的顺序排列，用三个数将观测值分成四部分，每一部分都包含25%的数据，这三个数就分别叫做第一四分位数（也叫第25百分位数）、第二四分位数（第50百分位数）和第三四分位数（第75百分位数），分别记作Q₁、Q₂和Q₃。显然，第二四分位数Q₂就是中位数。有25%的观测值小于Q₁；有25%的观测值大于Q₃；Q₁和Q₃给出了中间一半数据的范围。

利用找中位数的方法，就可以计算四分位数Q₁和Q₃。步骤如下：

（1）将观测值按从小到大的顺序排列，找出中位数M，即第二四分位数Q₂。

（2）找出中位数左边所有观测值的中位数，得到第一四分位数Q₁。

（3）找出中位数右边所有观测值的中位数，得到第三四分位数Q₃。

四分位数差就是Q₁和Q₃之间的距离：

IQR＝Q₃-Q₁

四分位数差克服极差易受到两端特殊值影响的缺点，是描述定序变量分布常用的统计量。

3.方差（Variance）和标准差（Standard Deviation）

对于定距变量和定比变量，描述分布最常用的统计量是均值和标准差，前者描述分布的中心，后者描述分布的离散程度。具体来说，标准差S表示观测值与平均数相离有多远；方差S²是标准差的平方。它们具体的计算方法如下：

方差S²

标准差S＝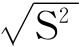

计算方差时所用的除数（n-1）常常被叫做自由度（df—degrees of freedom）。

方差或标准差的大小体现了观测值分布的离散程度：标准差越大，观测值的分布就越偏离分布的中心；反之，分布就越集中。

（四）斜度和峰度

描述定比或定距变量取值的分布，除了用描述中心和离散程度的统计量外，还常常需要考虑它们的形状。常用的方法是与标准正态分布相比较，标准正态分布是一种铃状的、对称的分布，如图3—1所示。

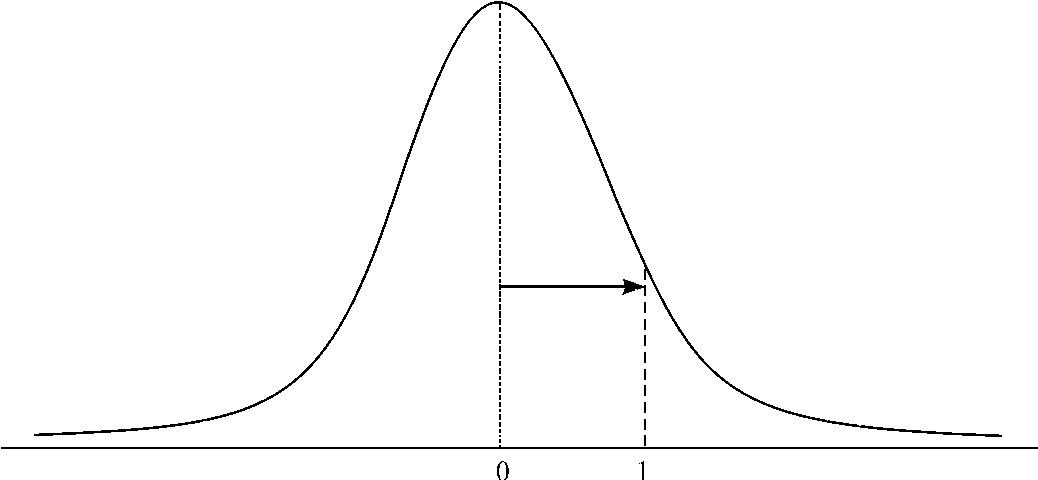
图3—1　标准正态分布曲线

1.斜度（skewed）

斜度也叫做偏度。一个分布如果是不对称的，即一端的样本观测值个数多于另一端时，则称该分布为偏斜的。斜度描述分布的偏斜程度和方向：如果分布是对称的，斜度为零；如果观测值集中在左侧，分布的右侧有一个长尾巴，则称正偏，斜度为正值；如果观测值偏向右边，左侧有一个长尾巴，则称负偏，斜度为负值；斜度的绝对值越大，偏斜程度也越大。图3—2给出了正偏和负偏的示意图。

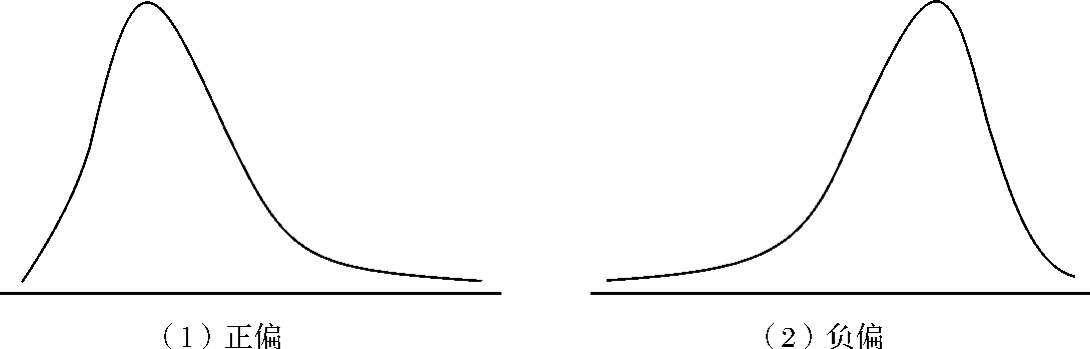
图3—2　分布的斜度

当分布接近正态分布时，根据标准差的大小，可以计算出观测值落入某个范围的比例有多大等信息，但如果分布和正态分布偏离较远或根本不是正态分布，计算就会不准确。因此，斜度实际上也是评价标准差准确性的一个度量。

2.峰度（kurtosis）

分布形状的另一特征用峰度来表示。峰度描述观测值聚集在中心的程度：如果观测值的中心聚集度与标准正态分布相同，或分布的形状与标准正态曲线的形状相同，则峰度为零；如果聚集度大于标准正态分布，即分布比标准正态曲线更陡峭，峰度为正；如果聚集度小于正态分布，即分布比标准正态曲线更扁平，峰度为负。图3—3给出了正峰度和负峰度的示意图。

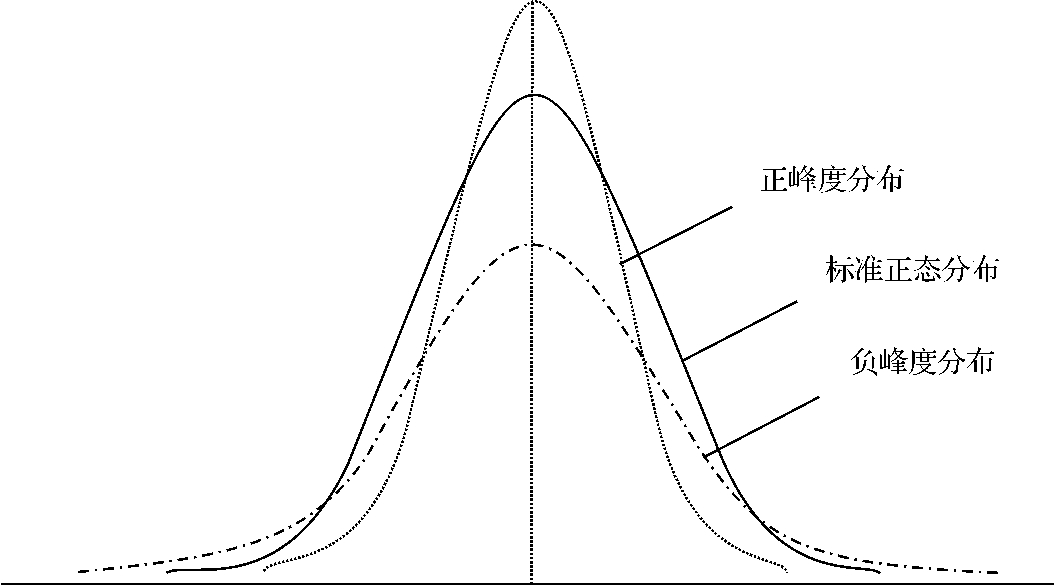
图3—3　分布的峰度

（五）相关系数

变量间的关系是媒介调查研究中十分关注的问题，例如实验法就是专门研究变量间关系的。在描述统计中，也常常考察变量间的相关关系，描述相关关系的统计量叫做相关系数（correlation coefficient）。

对于两个变量，如果随着变量X的增大，变量Y的值也同时出现增大或减小的趋势；反过来，随着变量Y的增大，变量X的值也同时出现增大或减小的趋势，则称变量X和Y之间存在相关关系。

不过，统计中所指的变量间的相关性或变大变小趋势，不同于数学中所表现的那种准确的数量关系，统计中的相关关系一般指的是在“平均来说”意义上的关系，就某些个体来说，可能并不具有这种规律性。

描述两个变量之间相关关系最常用的统计量是皮尔逊相关系数r，也叫积距相关系数，它适用于两个变量是定距变量或定比变量的情况，描述了两个变量之间的线性相关关系。

对于两个变量X和Y，如果这两个变量之一的值较大时，另一个变量的值也往往比较大；或另一个变量的值往往反而比较小，则这两个变量有线性相关关系（简称相关）。在前一种情况，称X和Y为正相关；后一种情况为负相关。

设变量X和Y共有n对观测值（X₁，Y₁）、（X₂，Y₂）、…、（X_n，Y_n），那么X和Y观测值之间相关系数r的计算方法是：

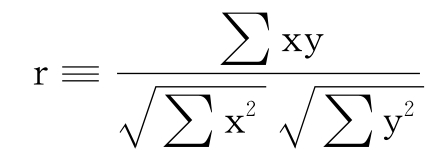
式中，符号≡表示定义；小写的字母x和y分别表示X和Y与其平均数的偏差，即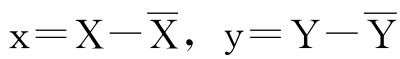；符号∑表示对n个数求和，为简化起见，省略了上下标。

图3—4给出了皮尔逊相关系数r的直观意义。

应当注意的是，皮尔逊相关系数r表现的是变量间的直线关联性，而变量间可能存在的曲线关联性是无法体现的。例如，在图3—4的（6）中，尽管X和Y存在明显的曲线相关，但是线性相关系数却等于零。在实际应用中，最好的方法是先对两个变量做类似这样的图，从图中看出变量间的关联趋势，再决定是否采用皮尔逊相关系数r描述其关联性。