第三节 指数体系与因素分析
一、指数体系的概念
社会经济现象存在普遍联系,这种联系可通过相应的指标体系表现出来。而很多指标体系可表达为经济方程式,而这里具有相乘关系的方程式大多可以转变为统计指标体系。如:
销售额(指数)=销售量(指数)*销售价格(指数)
总成本(指数)=产量(指数)*单位成本(指数)
社会保险收入(指数)=参保人数(指数)*交纳保险费额(指数)
粮食总产量(指数)=播种面积(指数)*单位面积粮食产量(指数)
利税额(指数)=销售额(指数)*销售价格(指数)*利税率(指数)
原材料消耗额(指数)=产量(指数)*单耗量(指数)*原材料价格(指数)
这里所讲的指数体系是指几个有关指数所结成的数量关系式,这种指数体系表现为:一个总量指数等于它的各个因素指数的乘积。这里所谓的“总量指数”通常是价值总量指数。显然,指数体系都是以客观现象之间的内在联系为基础。指数体系主要具有两个方面的作用。
1.用于指数之间的推算
根据指数体系,利用已知指数推算未知指数。例如,某地区本期与去年同期相比,居民消费的价格水平上涨3%,居民消费总额增加了8%,则居民消费数量指数为108%÷103%=104.85%,即剔除价格上涨因素后,居民消费实际增加了4.85%。
2.用于因素分析
以指数体系为基础,分析现象的总变动中各个因素的影响作用。在上节中,曾分析过综合指数计算结果的经济意义:它们不仅能够反映指数化指标的综合变动程度,也反映了指数化指标变动对相应总量的影响程度,其分子与分母之差则表示这种影响的绝对数量。所以,利用指数体系,可以对总量变动中各因素的影响效应一一进行分析。这种因素分析方法,不仅适合于两因素分析,也适合于多因素分析;不仅适合于对总量变动的分析,也适合于对总平均数(或相对数)变动的分析。下面将分别介绍其具体应用。
二、对总量的两因素指数分析
许多现象可以分解为两个因素的乘积,其一是数量指标,另一个则是质量指标。因此,分析该现象总量的变动,需计算三个指数:总量指数、数量指标指数和质量指标指数。为保证指数体系的成立,数量指标指数须采用拉氏公式,质量指标指数须采用帕氏公式。即:公式(13.9)。由此可以分析现象总量的变动程度中各因素的相对影响程度,还可以分析现象总量变动的绝对数量中各因素的影响数量(13.10)。
利用指数进行因素分析时,不仅要进行相对数分析,往往还需要进行绝对数分析,因此常常把也看做是指数体系的一个组成部分。
因素分析的一般步骤是:首先计算现象总量指数和总量变动的绝对差额;其次分别计算各个因素指数及其分子分母之差,用以反映各个因素对所研究总量变动的影响程度和影响数量;最后将以上分析进行综合和验证,作出文字分析说明。
[例13.2]根据表13.2的资料,对该城市社会保险缴费资料进行因素分析。
表13.2 某城市社会保险缴费资料
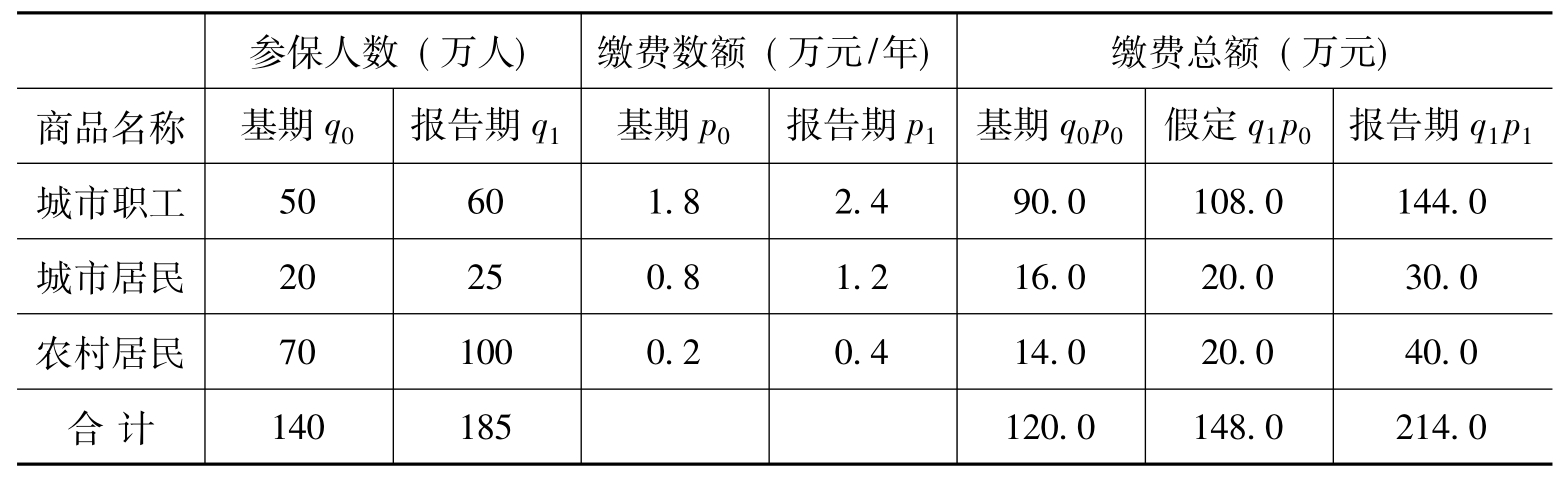
[解](1)分析:缴费总额=参保人数*缴费额;缴费总额指数=参保人数指数*缴费额指数。
(2)相对数指标体系:
参保人数指数:Iq=∑q1p0/∑q0p0=148/120=1.4459
缴费额指数:Ip=∑p1q1/∑p0q1=214/148=1.2131
于是可以构成综合指标体系如下:
∑p1q1/∑p0q0=Ip*Iq=(∑p1q1/∑p0q1)*(∑q1p0/∑q0p0)
214/120=(214/148)*(148/120);178.33%=144.59%*121.31%
(3)绝对数指数体系:
∑p1q1-∑p0q0=Ip-Iq=(∑p1q1-∑p0q1)+(∑q1p0-∑q0p0)
214-120=(214-148)+(148-120);94=66+28
(4)结论:报告期的社保基金比基期高78.33%,94万元,其中参保人员增加导致社保缴费增加44.59%,66万元;而由于社保缴费水平提高导致社保缴费增加21.31%,28万元。
用于因素分析的指数体系通常是指总指数体系。特殊地,若要分析单一个体的总量变动,所依据的是个体指数体系。由于只有单一个体,进行相对数分析时,不需要同度量因素;但进行绝对数分析时,同样必须考虑与之对应的数量指标或质量指标。因此,可将个体指数体系视为总指数体系的特例,依据个体指数体系进行因素分析的方法和步骤都与上述基于总指数体系的分析一致,只是计算公式中各项都不必含总和符号“∑”而已。
三、综合指数的平均数形式
总指数具有平均的性质,总指数反映的是全部个体变化程度的平均水平。有时,给出的仅是个体指数和基期或报告期的综合指数,这时需要有所变通。换另一种方法编制总指数:先计算出个体指数,再将个体指数加以平均即可求得总指数,这种方法计算的总指数也称之为平均指数。由于各个个体指数的重要性不同,所以平均指数通常都不能运用简单平均,而必须给个体指数赋予适当的权重进行加权平均。需要注意的是,这里计算的平均数指数和下一节计算的平均指数概念、计算方法等完全不同。
1.编制原理
编制平均指数有两大问题:
(1)采用哪种平均法,是算术平均法还是调和平均法?从实用的角度看,算术平均的方法计算较为简便,也比较直观,所以在计算总指数时,算术平均法的应用较为普遍。调和平均法,虽然计算较为复杂,也不太直观,但根据所掌握的数据和服从研究目的之需要,两者也有一定的实用价值。
(2)权数如何确定。权数的确定,既要考虑指数分析的实际经济意义,又要考虑权数资料获取的可行性和简便性。通常采用的权数主要有基期总值(q0p0)、报告期总值(q1p1)和固定权数(w)等三种。
由于对个体指数所采用的平均方法和所赋予的权数不同,平均指数的计算又有多种不同的方法,下面将分别予以简要介绍。
2.综合指数的平均数形式
综合指数的平均数形式,是用平均数形式来表示综合指数,不同于第四节所分析的“平均指标变动因素分析”。算术平均指数是将个体指数(q1/q0)进行算术平均来求得的总指数,其权数一般有基期总值(q0p0)和固定权数(w)两种。
(1)算术平均指数
基期总值(q0p0)加权的数量指标平均指数的计算公式为:
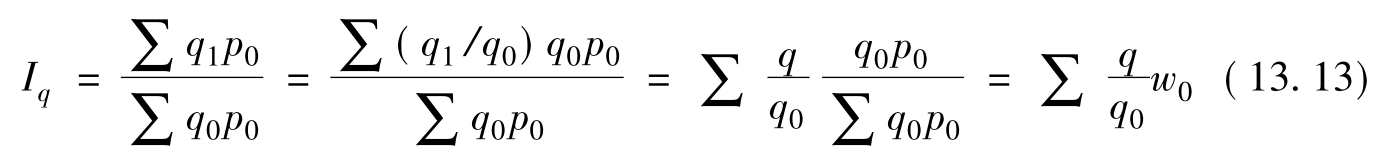
式中:w0为基期总值的比重,即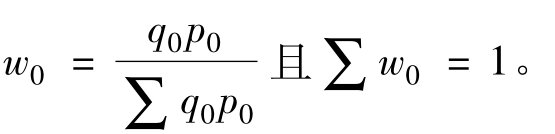
[例13.3]某企业生产三种产品的产量(q)和出厂价格(qp)如下,利用加权算术平均指数的公式来计算三种商品的产量总指数。
表13.3 某企业生产三种产品的产量总指数计算
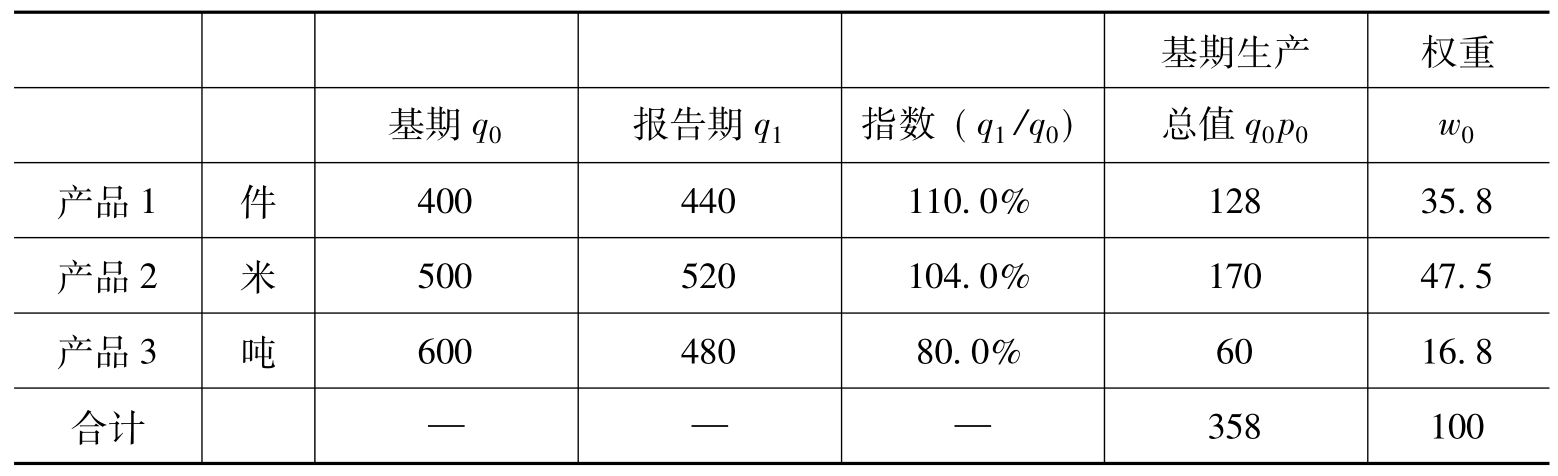
[解]先根据上表资料计算出三种商品的产量个体指数(q1/q0分别为110%、104%和80%)及基期销售额加权,即可得销售量总指数如下:
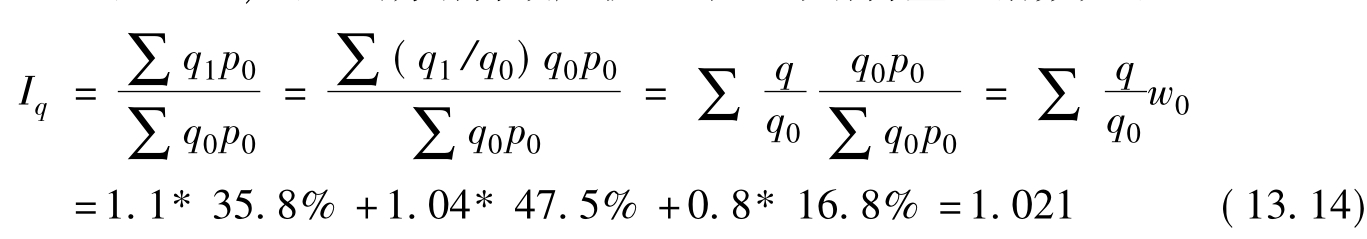
即该企业报告期产量与基期相比,综合上升了2.1%。上述结果与前面由拉氏指数公式得到的计算结果相同。实质上,当个体指数与其对应权数两者的计算范围都完全一致时,基期总值加权的算术平均指数是拉氏综合指数的变形,两者只是计算形式不同,而计算结果和经济意义都完全相同。
(2)调和平均指数
调和平均指数是将个体指数(p1/p0)进行调和平均来求得的总指数,通常采用报告期总值(m)为权数。其计算公式为:
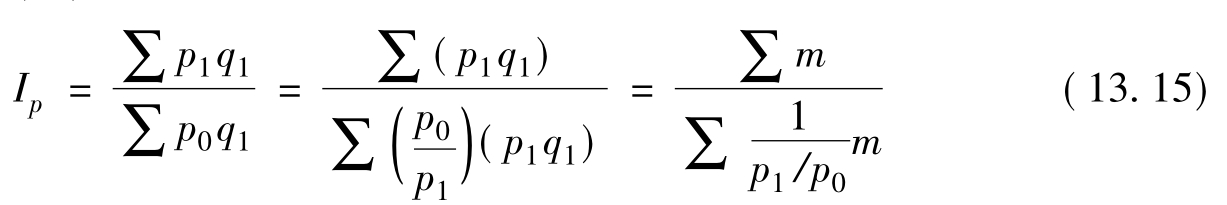
式中:m=p1q1。
[例13.4]某企业生产三种产品的价格(p)和生产总值(qp)见表13.4,利用加权调和平均指数的公式来计算三种商品的价格指数。
表13.4 某企业生产三种商品的价格指数计算
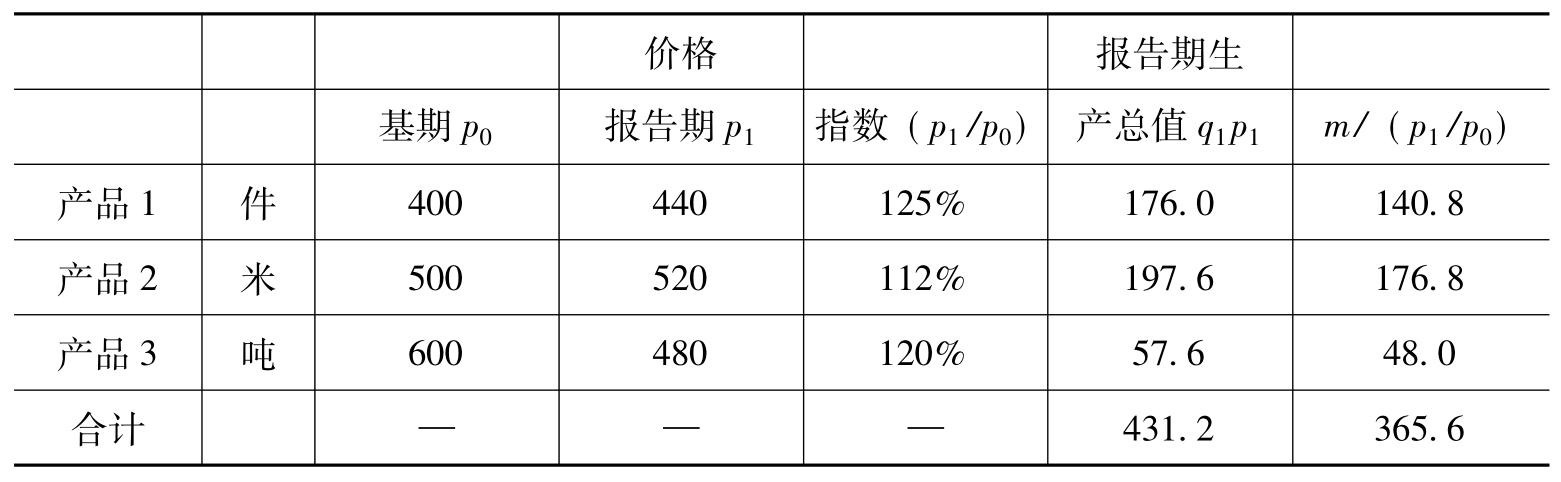
[解]先根据上表资料计算出三种商品的价格个体指数(p1/p0分别为125%,112%和120%)。再以基期销售额加权,于是可得价格总指数如下:
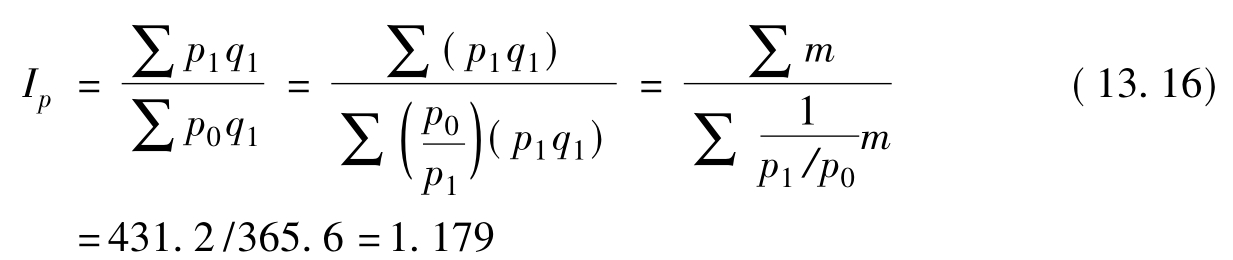
即该企业报告期价格与基期价格相比,综合上升了17.9%。该结果与由帕氏指数公式计算的结果相同。实质上可证明,当个体指数与其对应权数两者的计算范围都完全一致时,报告期总值加权的调和平均指数是帕氏综合指数的变形,两者只是计算形式不同,而计算结果和经济意义都完全相同。
(3)固定权数的算术平均指数
统计实践中编制算术平均指数时,常常将权数(通常是指比重权数)相对固定,即在较长时间保持不变。其计算公式为:
![]()
式中:w为固定比重权数,∑w=1(100%)。
固定权数的平均指数具有很多优越性,它不仅计算简便,而且也排除权数变动对总指数的影响,还可以很方便地进行环比指数与定基指数之间的推算。我国居民消费价格指数就是采用这种方法编制的。
四、对总量的多因素指数分析
当所研究的现象分解为三个或三个以上因素的乘积时,分析各个因素变动对该现象总变动的影响就属于多因素分析。指数体系用于两因素分析的基本原理可以推广到多因素分析,其要点如下:
(1)各因素的分解和排列:要体现指标之间的相互关系,即要保证相邻指标两两相乘都有经济意义。这种顺序的合理性,既有利于正确区分数量指标和质量指标,保证指数体系的成立,也便于将有关因素合并或进一步细分。通常的顺序是先基础指标,后派生指标;或先数量指标(外延指标),后质量指标(内涵指标)。在多因素分析中,数量指标与质量指标的划分不是绝对的,而是两两相对的,要根据指标的内容和各因素之间的联系来判断。换言之,中间指标与前一个指标相乘为数量指标,与后一个指标相乘为质量指标,各指标都要有相互独立的经济或社会意义。这看似做数学游戏,实际通过分解,可以看出各指标的影响大小和影响方向。例如:
材料消耗总额=产量*(总耗材/产量)*(总价格/总耗材)
材料消耗总额=产量*单位产品消耗量*材料价格
社保缴费总额=参保人数*(总工资/参保人数)*(总缴费额/总工资)
社保缴费数额=参保人数*名义工资*缴费费率
农作物总收益=播种面积*(总产量/播种面积)*(总价格/总产量)
农作物总收益=播种面积*单位面积产量*农作物价格
(2)转变成指标体系:测定其中某个因素的影响时,须将其余所有因素都固定下来。
(3)将数量(前已经研究过的)指标固定在报告期,同时将质量(未研究过)指标固定在基期。
在遵循上述排序原则的前提下,测定某个影响因素变化的影响时,排列在它之前的指标都看作数量指标,固定在报告期;排列在它之后的指标都看做是质量指标,固定在基期。这样,在形式上,对各因素的影响程度的测定,就相当于依次对各影响因素进行连锁替代和对比。因此,多因素的指数分析方法也常常被称为“连锁替代法”,意即在基期总量的基础上,依次将其中各因素的基期数替代为报告期数,并将替代后的总量与替代前的总量相比,即得该因素的总指数——反映该因素的平均变动程度及其对所研究现象总量的影响程度,其分子分母差额表示该因素变动对所研究现象的绝对影响额。
假设所研究现象总量F可分解为q、m和p三个因素,其关系为F=q*m* p。连锁替代法的具体过程如下:基期总量∑q0m0p0,第一次替代(将q0替换为q1)得到∑q1m0p0,第二次替代(在第一次替代的基础上将m0替换为m1)得到∑q1m1p0,依次类推,最后一次替代后得到报告期总量∑q1m1p1。将每一次替代后与替代前的两个总量进行对比,所得指数即可料定此次替代因素对所研究现象总量的影响程度,这两个总量的差额也就反映此次替代因素的绝对影响量。例如,将第二次替代前后的两个总量对比即∑q1m1p0/∑q1m0p0,这个比率就是测定因素m综合变动的程度及其对所研究总量F影响程度的指数,(∑q1m1p0-∑q1m0p0)就表示因素m变动使所研究现象F增减的数量。依次类推,可分析其余各因素的影响。
[例13.5]已知某公司三种商品的销售资料如表13.5所示,试对该公司三种商品的销售利润总额的变动进行因素分析。
表13.5 某公司三种商品的因素分析
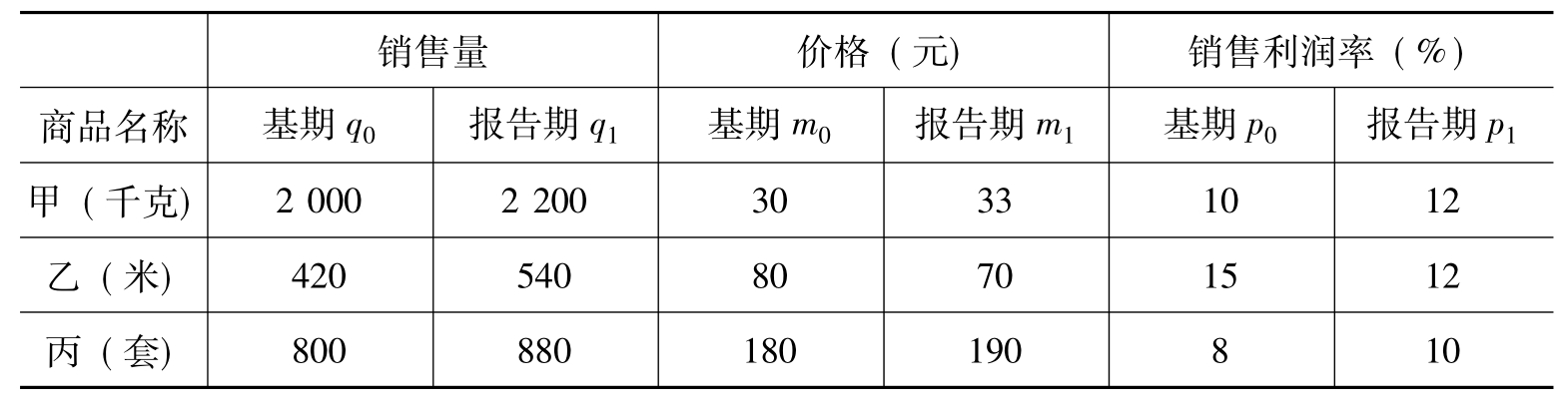
[解]总利润额=销售量*总销售额/销售量*总利润额/总销售额
总利润额(qmp)=销售量(q)*单位商品销售价格(m)*销售利润率(p)
根据上述关系,对利润总额的因素分析应以下列指数体系为依据:
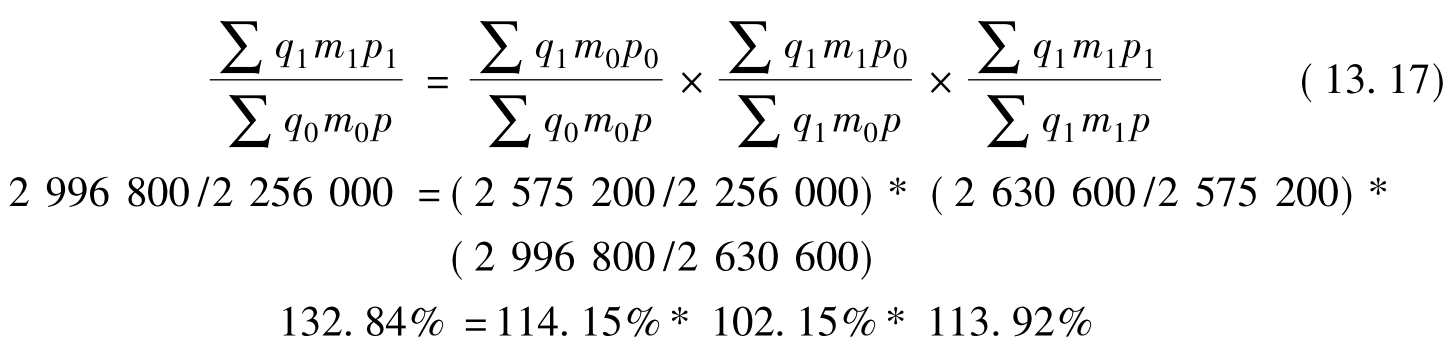
以上几个计算结果之间的关系为:
∑q1m1p1-∑q0m0p=(∑q1m0p0-∑q0m0p)+(∑q1m1p0-∑q1m0p)+(∑q1m1p1-∑q1m1p)
2996800-2256000=(2575200-2256000)+(2630600-2575200)+(2996800-2630600)
740800=319200+55400+366200(元)
计算结果表明,三种商品的利润总额增长32.84%,即增加740800元。其中,由于三种商品的销售量增长而使利润总额增长14.15%,即增加319200元;由于商品价格因素变化而使利润总额增加2.15%,增加55400元;由于销售利润率上升而使利润总额增加13.92%,增加366200元。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














