变量与函数目标确定依据

1．线性规划问题

1.1线性规划的基本概念

（1）线性规划的含义

线性规划是在有限资源的条件下，合理分配和利用资源，以期取得最佳的经济效益的优化方法。线性规划由一组有待决策的变量（Decision variables），一个线性的目标函数（Objective function），一组线性的约束条件（Constraints）构成三要素。如果在规划问题的数学模型中，变量是连续的（数值取实数），其目标函数是有关线性函数（一次方），约束条件是有关变量的线性等式或不等式，这样，规划问题的数学模型是线性的。反之，就是非线性的规划问题（其中一个条件符合即可）。

（2）线性规划模型的特征

①解决问题的目标函数是多个决策变量的线性函数，通常是求最大值或最小值；

②解决问题的约束条件是一组多个决策变量的线性不等式或等式。

（3）线性规划解决的问题

线性规划通常解决下列两类问题：

①当任务或目标确定后，如何统筹兼顾，合理安排，用最少的资源（如资金、设备、原标材料、人工、时间等）去完成确定的任务或目标；

②在一定的资源条件限制下，如何组织安排生产获得最好的经济效益（如产品量最多、利润最大。

1.2线性规划问题

（1）生产计划问题

例3.1某企业生产三种产品，这些产品分别需要甲、乙两种原料，生产每种产品一吨所需原料（吨）和每天原料总限量（吨）及每吨不同产品可获利润（千元/吨）情况如表3.1所示。

表3.1

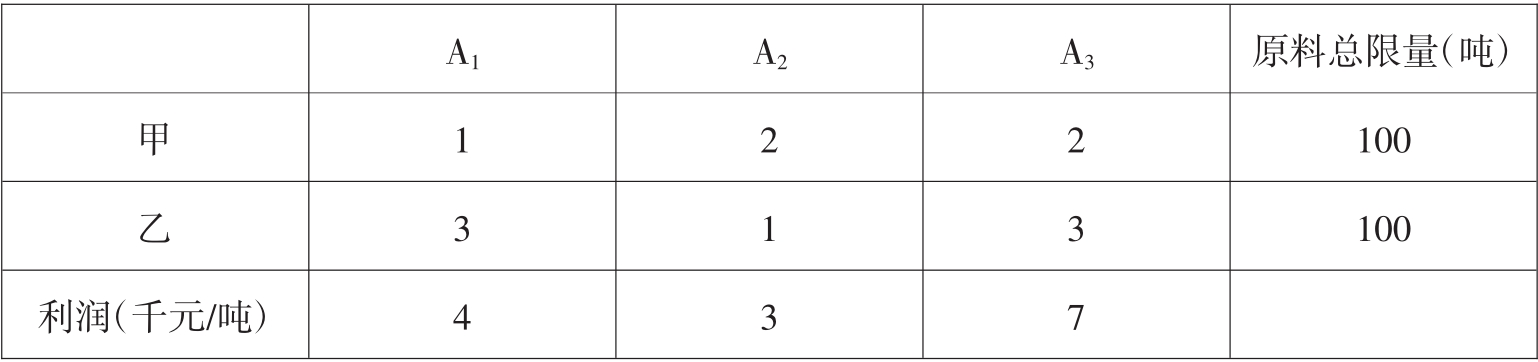
试问，该企业怎样安排生产，才会使每天的利润最大?

所谓“怎样安排生产”，意指A₁、A₂、A₃三种产品各生产多少吨。每指定一次三种产品的产量，就决定了一个生产方案，而一个生产方案决定一个获利值，称为目标函数。现在追求的目标是获利最大。

设x₁，x₂，x₃分别表示A₁、A₂、A₃三种产品的产量，它们是决策中的关键变量，这种变量称为决策变量，它们都是非负的。

目标函数Z=4x₁+3x₂+7x₃

它是决策变量的函数。x₁，x₂，x₃受到甲、乙两种原料的限制，即：

x₁+2x₂+2x₃≤100

3x₁+x₂+3x₃≤100

综上所述，有

MaxZ=4x₁+3x₂+7x₃

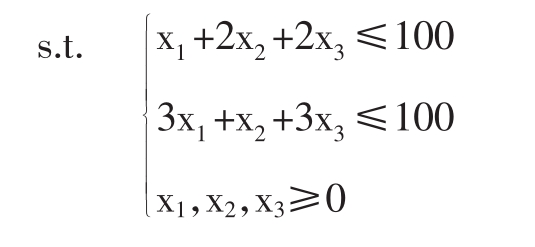
其中“s.t.”为英文“subjectto”（受约束于）的缩写。

（2）下料问题

例3.2现有一批长度一定的原材料钢管，由于生产的需要，要求截出不同规格的钢管若干。试问应如何下料，既能满足生产的需要，又使得使用的原材料钢管数量最少（即废材最少）?

具体问题：料长7.4m，要求截成2.9m，2.lm，1.5m的钢管分别为1000根，2000根，1000根。如何截取，才使得总用料最省?

首先分析，把一根7.4m长的钢管截成2.9m，2.lm，1.5m三种规格的钢管，共可设计下列5种比较经济的下料方案，结果见表3.2.。

表3.2

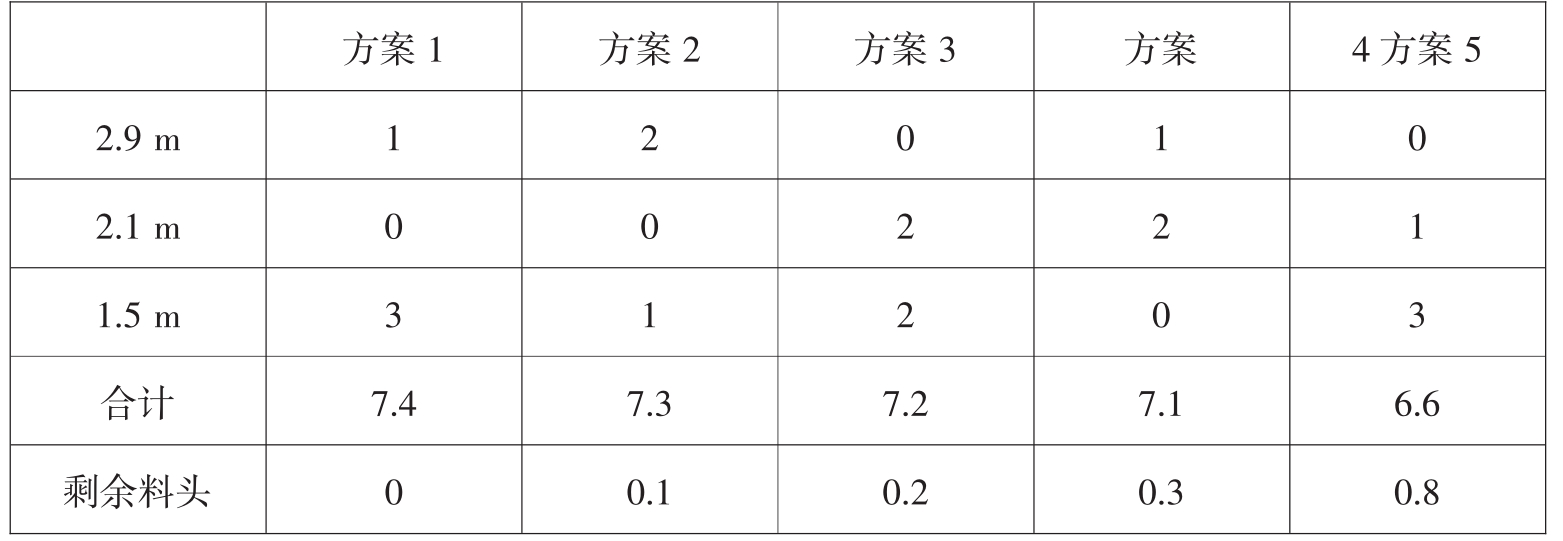
设x₁，x₂，x₃，x₄，x₅分别为上面5种方案下料的原材料根数。这样我们建立如下的数学模型。

注意：在建立此类型数学模型时，约束条件用大于等于号比用等于号要好。因为有时在套用一些下料方案时可能会多出一根某种规格的圆钢，但它可能是最优方案。如果用等于号，这一方案就不是可行解了。

（3）配料问题

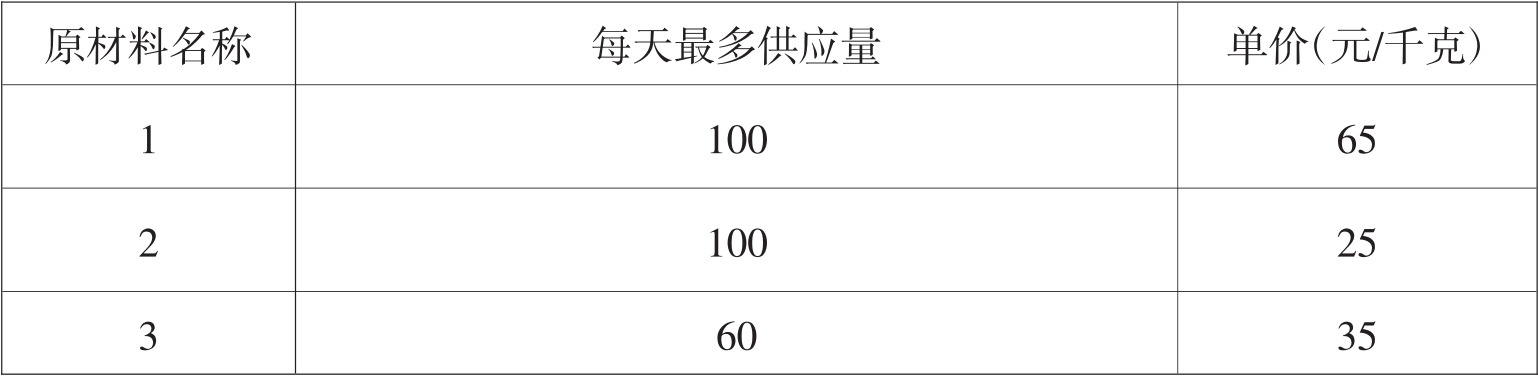
例3.3某工厂要用三种原料1、2、3混合调配出三种不同规格的产品甲、乙、丙，数据表3.3和表3.4。问：该厂应如何安排生产，使利润收入为最大？

表3.3

表3.4

设x_ij表示第i种（甲、乙、丙）产品中原料j的含量。这样我们建立数学模型时，要考虑：

对于甲：x₁₁，x₁₂，x₁₃；对于乙：x₂₁，x₂₂，x₂₃；对于丙：x₃₁，x₃₂，x₃₃；

对于原料1：x₁₁，x₂₁，x₃₁；对于原料2：x₁₂，x₂₂，x₃₂；对于原料3：x₁₃，x₂₃，x₃₃；

目标函数：利润最大，利润=收入－原料支出

约束条件：规格要求4个；

供应量限制3个。

利润=总收入－总成本

=甲乙丙三种产品的销售单价×产品数量－甲乙丙使用的原料单价×原料数量，故有：

目标函数

MaxZ=50（x₁₁+x₁₂+x₁₃）+35（x₂₁+x₂₂+x₂₃）+25（x₃₁+x₃₂+x₃₃）－65（x₁₁+x₂₁+x₃₁）－25（x₁₂+x₂₂+x₃₂）－35（x₁₃+x₂₃+x₃₃）=－15x₁₁+25x₁₂+15x₁₃－30x₂₁+10x₂₂－40x₃₁－10x₃₃

约束条件：

从表3.3中有：

x₁₁≥0.5（x₁₁+x₁₂+x₁₃）x₁₂≤0.25（x₁₁+x₁₂+x₁₃）x₂₁≥0.25（x₂₁+x₂₂+x₂₃）x₂₂≤0.5（x₂₁+x₂₂+x₂₃）

从第3.4个表中，生产甲乙丙的原材料不能超过原材料的供应限额，故有：

（x₁₁+x₂₁+x₃₁）≤100（x₁₂+x₂₂+x₃₂）≤100（x₁₃+x₂₃+x₃₃）≤60

通过整理，得到以下模型：

（4）人员安排问题

例3.4某昼夜服务的公交线路每天各时间段内所需司机和乘务人员数如表3.5

表3.5

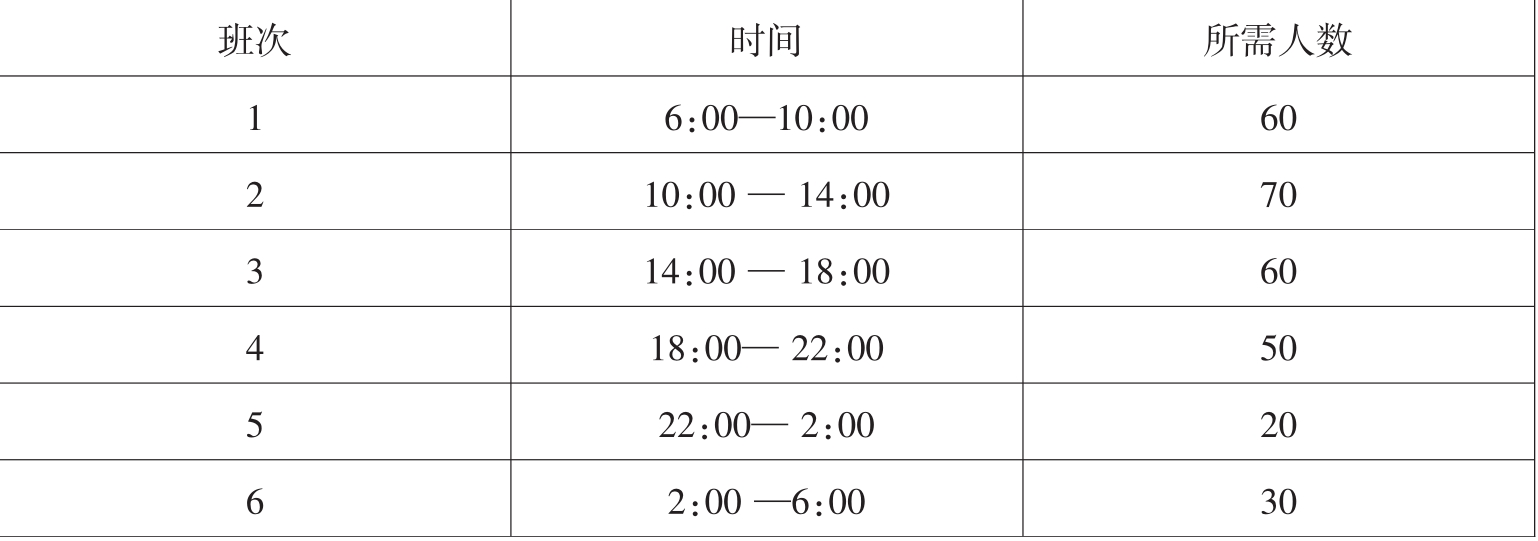
设司机和乘务人员分别在各时间段一开始时上班，并连续工作八小时，问该公交线路怎样安排司机和乘务人员，既能满足工作需要，又配备最少司机和乘务人员?

设xi表示第i班次时开始上班的司机和乘务人员数，这样我们建立如下的数学模型。

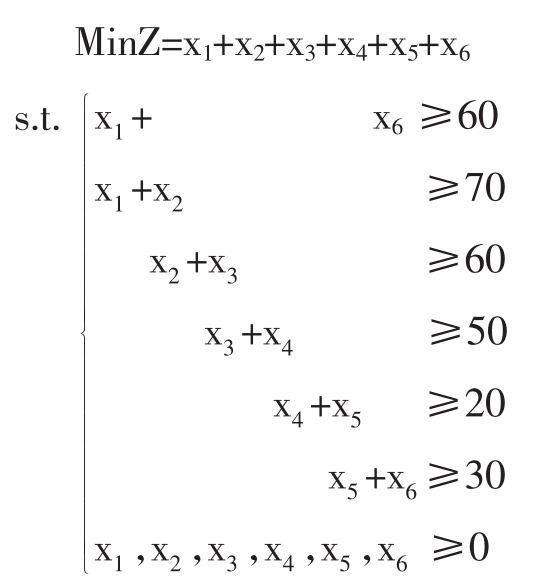
（5）运输问题

例3.5设仓库A1、A2每月可以分别调出某种商品28吨、29吨，零售店B₁、B₂、B₃每月需要这种商品分别为12吨、15吨、30吨，所需商品均由仓库A₁、A₂供应。各仓库运往各零售店的运费如表3.6。如何安排运输计划，可使总运费最少？

表3.6

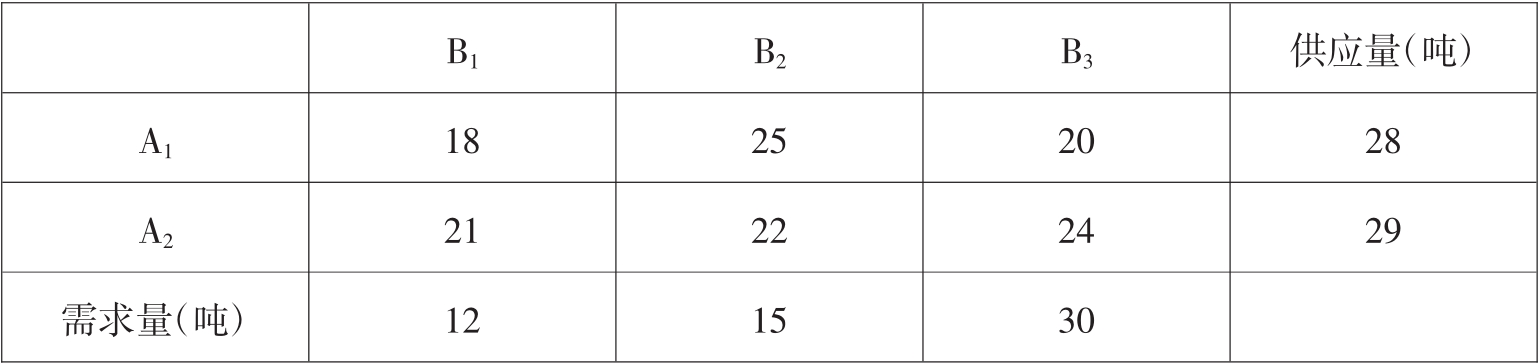
设x_ij表示仓库Ai向零售店Bj调运商品的数量（i=1，2；j=1，2，3），则模型为：

上述各例的实际背景尽管不同，但是它们的数学模型具有共同的特征：

①目标函数是多个决策变量的线性函数，通常是按问题的不同，求最大值或最小值；

②约束条件是决策变量的线性不等式或等式。