大自然的数学情趣

第三节　大自然的数学情趣^[3]

《全日制义务教育数学课程标准（实验稿）》在课程的总体目标中强调通过数学学习，学生要体会数学与自然及人类社会的密切联系，了解数学的价值，增进对数学的理解。而自然界中的许许多多物种都以数学的方式表现出其特性。你有没有观察过一片叶子，对它为什么能精确地分成两半表示奇怪？你有没有注意到各种花的花瓣形成的完美星形？有没有注意到某些贝壳和松果的螺旋形生长模式？有没有注意到人的头发或红杉树的树枝、树皮的生长模式？自然界中充满着数学概念的众多实例。大自然的数学情趣高雅无比，精妙无穷。

一、树叶与花瓣上的数学

花瓣图案和树叶在枝干上生长的方式，使数学家认识到，斐波那契数列1，1，2，3，5，8，13，…，在自然界中随处可见。如果我们去数一根枝条上的树叶，从某一片叶子开始，到其正上方的一片叶子为止，两者之间的叶子数通常是一个斐波那契数。

斐波纳契数列并不是数学家们的臆造，已经发现在自然界中有许多现象符合斐波纳契数列的规律。特别在植物世界中，几乎所有的花卉的花瓣基数是斐波纳契数。如桂花（图1-3-1）是2基数的，兰花（图1-3-2）、鹤望兰（图1-3-3左上）和嘉兰（图1-3-3左下）都是3基数，梅花、凤凰木（图1-3-3右上）和扶桑（图1-3-3右下）等是5基数。再如，松树的针叶数只有：两针松（图1-3-4）、三针松以及五针松，没有四针松。

图1-3-1　中国邮票（1995）

图1-3-2　中国邮票（2001）

图1-3-3　美国小本票（1998）

图1-3-4　苏联邮资封（1986）

斐波那契数列的相邻两项之比1/1，2/1，3/2，5/3，…，趋于一个极限，通常称为“黄金比例”，等于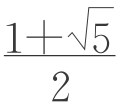＝1.618…。这个比例在整个数学中都随处可见：它是正五边形的一条对角线和一条边之比，并且边长为这一比例的矩形通常被认为是最令人满意的形状——黄金矩形。图1-3-5是一个黄金矩形，在这个黄金矩形中分出一个正方形，位于左边，右边剩下的仍是一个小的黄金矩形。在这个黄金矩形中再分出一个正方形，位于上边，下边剩下的是一个更小的黄金矩形，把这个过程继续下去，现在我们用一条光滑的连续曲线把所有正方形的顶点连起来，得到的就是对数螺线或等角螺线（图1-3-6）。海螺、蜗牛的外形就非常近似于对数螺线。图1-3-7的瑞士邮票就表现了这一过程，还有在蜗牛壳和菊石（图1-3-8）上也出现了与此紧密相关的对数螺线图案。进一步指出的是，非洲大羚羊的角、金银花的螺旋线、贝壳的漩涡、银河系的螺线、DNA的双螺旋，在这些例子里我们可见到的递归曲线，说明螺旋线能适应生长。

图1-3-5

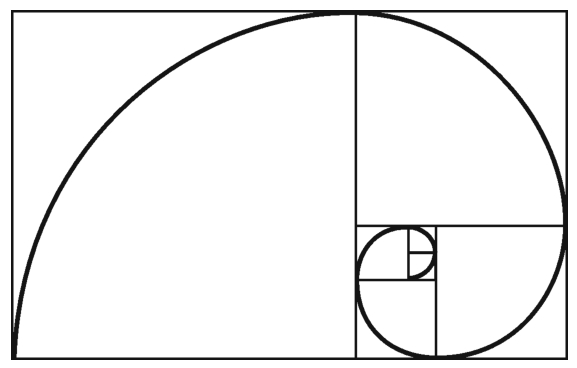
图1-3-6

图1-3-7

图1-3-8

三、蜘蛛网上的数学

一种简洁而优美的自然物——蜘蛛网（图1-3-9），在晨曦的照射下那挂满露珠的网散射着光辉，沁人心脾，令人陶醉！蜘蛛网有片状的、三角形状的、漏斗状的或圆顶状的，不同形状的蜘蛛网由各种不同的蜘蛛织成。当人们仔细观察，试图准确地描述这美妙的结构时，发现只有用复杂的数学公式才有可能。

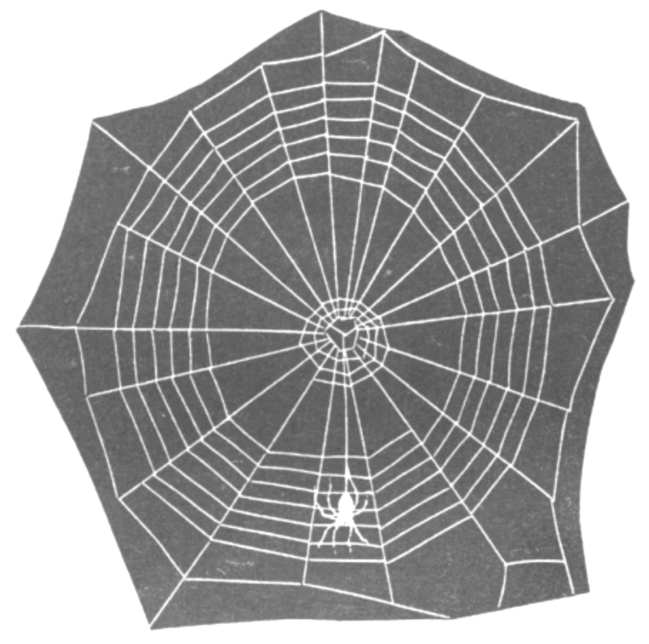
图1-3-9

在蜘蛛网中，人们首先注意到的数学对象大概是两条类似于螺线的蛛网曲线。我们把从蛛网中心放射出去的那几条线称为“半径”。类似螺线的曲线则由连接两相邻半径的弦形成。位于两条相邻半径间的弦互相平行，沿半径的所有同位角全都相等。假如蜘蛛网的半径有无穷多条，那么整段蜘蛛网将具有单一的形式，这时替代锯齿般螺形线的是一条平滑的曲线。这种曲线就是对数螺线，即等角螺线。从等角螺线的性质可以知道这种类似于螺线的蛛网，既经济又规则地充满了空间，它不仅强韧而且用料最少。

当早晨的露凝布在蜘蛛网时，互相靠拢的水结成小小的水滴（特别对于较黏的丝）。蛛网的弦由于水滴的负荷而弯曲，使得每条弦都变成为悬链线！

悬链线是由一条自由悬挂着的柔软的绳子或链条所形成的曲线（图1-3-10），它的一般方程为：

这里a是Y轴上的截距。

出现在悬链线方程的e为：

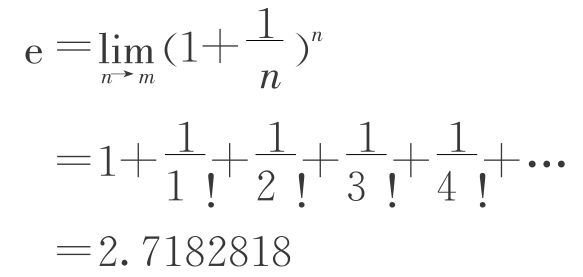
它是一个无理数和超越数，也算是一件被蜘蛛网“捕捉”的“猎物”。蜘蛛网上还有许多其他的数学概念，如半径、弦、平行线段、三角形、相等的同位角、等数螺线、悬链线等，也和e一样都“落入”了蜘蛛所编织的陷阱。

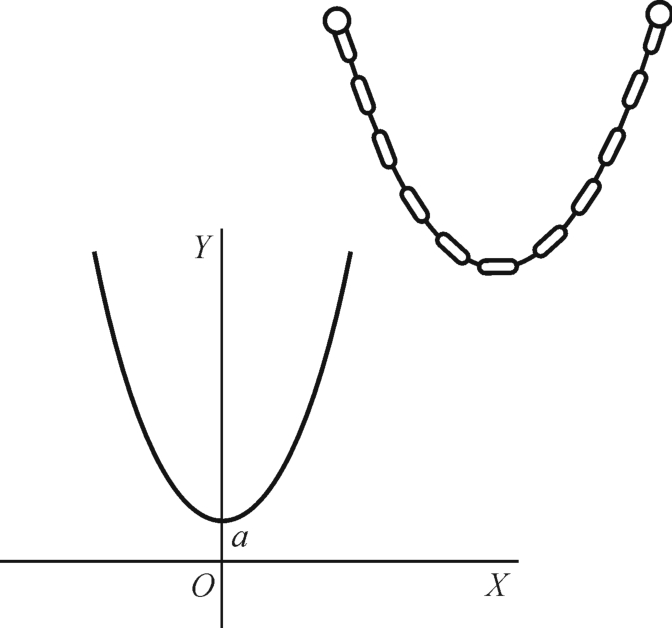
图1-3-10

三、蜂房中的数学

卢森堡的一张蜂巢邮票反映的是小小蜜蜂建造的蜂房（图1-3-11），这是最为普通的一种平面镶嵌图案，即用同样形状的平板砖，无缝隙而又不重叠地铺满整个平面。事实上，公元前4世纪古希腊的数学家帕普斯就观察到：蜜蜂只用正六边形制造它们的巢室，这种形状的构造会使所需的材料最少，而且所形成的空间最大。六边形的形状不仅可以在蜂巢中找到，还可以在雪花、分子、晶体、海洋生物等其他形式的物体中找到。类似蜂房的这种镶嵌图案，人们可能早已看到过，如用等边三角形或正方形形成的镶嵌图案。事实是，古希腊毕达哥拉斯学派早已发现并证明了在正多边形中仅有正三角形、正方形和正六边形这三种可以形成镶嵌平面，而且对于给定面积来说，六边形的周长最小。有人认为毕达哥拉斯学派对正多面体的研究工作是平面问题在空间的推广，而阿基米德又进一步深入到构造半正多面体。正是这种只需花费最少能量和材料的形式，把自然界和数学联系起来——自然界掌握了解极大极小问题、线性代数问题和求出含约束问题最优解的艺术，真不愧是自然界中的美妙数学问题！当然，在平面镶嵌中，我们还可以用任意同样的三角形、四边形来形成镶嵌图案。

图1-3-11　蜂巢（卢森堡）

四、更多的实例

在晶体、岩层和珠宝表面，可以看到多面体形态，由此导致科学家将晶体按其形状和对称性来分类。

研究江河溪流的扭转、弯曲、变向，看似毫无章法，其实可以发现，它们的形状表明，水流的两点之间的最短距离未必决定水流方向，它们的自然弯曲受离心力和能量均衡消耗的支配，并可用随机性和概率描述。

一串肥皂泡沫、犰狳的鳞片、泥地的裂缝、玉米棒的芯、某些树的树皮、长颈鹿身上的花纹、蜂窝格子、美国加利福尼亚州魔鬼堆国家景区岩石的形状，在这些场合里见到的形态，提供了六边形、三叉连接和紧密填装观念的例证。

风吹沙滩的痕迹、云朵的姿态、火山熔岩流淌的形状、山脉蜿蜒的地势、蕨类植物叶形的重复，在这些例子里出现的图案，都能被数学家利用计算机和分形方程再现出来。如今通过计算机，分形数学理论已经发展到新的水平，而且不断发现新应用以及它与自然的新联系。

龟壳上片状组织的构造，以及丝织物的纤维类似于三棱柱，这样的结构使丝显得富有光泽。

参考文献

［1］［英］罗宾・J．威尔逊．邮票上的数学［M］．李心灿，邹建成，郑权译．上海：上海科技教育出版社，2002：98－99．

［2］［美］T．帕帕斯．数学趣闻集锦（下）［M］．张远南，张昶译．上海：上海教育出版社，1998：329－331．

［3］张维忠．文化视野中的数学与数学教育［M］．北京：人民教育出版社，2005：167－168．

［4］［美］T．帕帕斯．数学走遍天涯——发现数学无处不在［M］．蒋声译．上海：上海教育出版社，2007：100－101．