稳定性的基本概念

1）稳定性定性定义

稳定性的简单定义就是系统在外部扰动作用下偏离其原来的平衡状态，当扰动作用消失后，系统仍能自动恢复到原来的初始平衡状态，则称系统是稳定的，否则称系统是不稳定的。

如图4-4所示的两个单摆，竖直位置是它们的平衡位置。如果以平衡位置为初始位置分别对球施加水平外力，图4-4（a）中的单摆在多次摆动后会回到初始位置，而图4-4（b）的单摆则永远不会回到初始的竖直状态。

图4-4 单摆

如果将外部的扰动视为脉冲输入，则可以从系统的脉冲响应来判定其是否稳定。图4-5所示为一些系统的脉冲响应，系统初始平衡状态均为零。当对它们施加如图4-5（b）所示的扰动脉冲信号后，输出量y（t）开始偏离初始平衡位置。当扰动脉冲消失后，如图4-5（c）所示，系统1、2输出量最后仍回到初始零位，系统1、2是稳定系统。图4-5（c）中系统3输出呈现等幅振荡，系统4输出呈发散状，两个系统都不能恢复到初始零位，系统3、4是不稳定系统。

图4-5 系统的脉冲响应

上述稳定性的粗略定义只适用于线性定常系统。如某些非线性系统可能在小扰动作用消失后能恢复到原平衡位置，但在大扰动作用消失后系统不能恢复到原平衡位置，即系统在小范围内稳定。又如某些非线性系统在扰动作用消失后，系统不能恢复到原来的平衡位置，而能在新的平衡位置稳定地工作。图4-6是对大范围稳定与不稳定、小范围稳定、临界稳定的一个形象表达，其中临界稳定是稳定与不稳定的边界，稳定性分析中用稳定性裕量来量化到达临界稳定边界。俄国学者李亚普诺夫提出了系统稳定性严格而普遍适用的定义，但本书仅对线性定常系统展开稳定性分析，线性定常系统的大范围稳定与小范围稳定是一致的。

图4-6 稳定性的形象表达

（a）大范围稳定； （b）临界稳定； （c）大范围不稳定； （d）小范围稳定

2）系统稳定的充分必要条件

设系统的传递函数为

令系统特征方程D（s）＝0，假定系统特征方程的根中有k个实根pi（i＝1，2，…，k）， 2l个共轭复根pj、＝σj±jωj（j＝1，2，…，l），则上式可写成

若输入为脉冲函数r（t）＝δ（t），当作用时间t＞0时，r（t）＝0，相当于扰动消失。

将系统输出量C（s）写成部分分式

对上式拉氏反变换，可得扰动为理想脉冲函数作用下的系统输出

由上式可知，如果pi和σj均为负值，则当t→∞时，c（t）→0，说明当系统特征方程根是负实根或共轭复根具有负实部时，系统在扰动消失后能恢复到原平衡状态c（t）∣t＝0＝0，即系统稳定。

根据上面分析可得出：动态系统稳定的充分必要条件是系统特征方程的根全部具有负实部，即闭环系统的极点全部在s平面左半部。

如图4-7所示的两个单摆系统，直觉可知图47（a）是一个稳定系统，图4-7（b）是一个不稳定系统。对于图4-7（a）有

图4-7 单摆系统

式中M、L为杆件的质量和杆长。

当角度θ为很小的值时，有

对应有传递函数

其极点为

如图4-7（c）所示，此两个极点处于s平面虚轴上，即临界处，如果计入空气阻力带来的阻尼项，则极点将落入s的左半平面（图中的阴影处）即稳定区域。

对图4-7（b）建模可得到

其极点为

为两个实数极点。如图4-7（c）所示，其中一个为正实根，位于s的右半平面，即不稳定区域。

不稳定的闭环反馈系统在实际应用中实用性不大。许多开环不稳定的物理系统可以通过反馈环节使系统稳定，并在稳定的前提下选择控制器参数，调节系统瞬态性能。

除了稳定或不稳定的绝对稳定性判定，还需衡量稳定程度即相对稳定性，以应对系统建模中忽略的非线性因素和一些性能的小时变。相对稳定性体现在稳定性与快速性的综合考量中，极点离虚轴越远系统越稳定，但极点离虚轴越近响应越快。如飞行器尤其是战斗机中的机动性设计中，会故意设计成开环不稳定以提高快速性，再通过反馈系统协助飞行员的操纵。

图4-8 正反馈系统

从稳定性出发控制系统的反馈回路应是负反馈。如图4-8所示是一个有正反馈回路的闭环系统，传递函数，当G（s）H（s）＝1时，C（s）＝∞·R（s）；当r（t）≡0时，系统输出c（t）＝0；但当r（t）稍有扰动时，系统输出c（t）随即不为零，并通过正反馈放大，直到物理系统达到饱和状态。

不稳定的开环系统反馈后可能稳定工作，但闭环系统不等同于稳定系统。如果反馈回路中控制器的类型选用、控制器参数选择不合理，可能会将一个稳定的开环系统变成一个不稳定的系统。

［例4-02］ 单位反馈系统的开环传递函数为G（s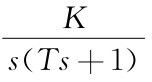）＝（K＞0，T＞0），请判断系统稳定性。

［解］ 闭环传递函数

可得判别系统稳定性的特征方程如下

Ts2＋s＋K＝0

特征方程的根

由此式知：

（1）KT＜1／4时，特征方程有两个不同的负实根；

（2）KT＝1／4时，特征方程有一个负实根，一个零根；

（3）KT＞1／4时，特征方程有一对具有负实部的共轭复根。

即KT不断增长的过程中特性方程的根始终在s平面的左半面（含KT＝1／4对应的虚轴），所以系统是稳定的。

上述二阶系统例子中特征根求取较容易。工程上遇到的往往是高阶系统，此时可借助计算机软件求解高阶系统特征方程的根。在MATLAB中可以调用roots（）函数求取特征多项式的根，然后由系统稳定性的充要条件，即系统特征方程的根全部具有负实部进行系统稳定的判别。

［例4-03］ 系统特征方程s5＋6s4＋2s3＋3s2＋2s＋6＝0，试判断该系统的稳定性。

［解］ MATLAB中程序为

MATLAB运行结果为

可见有两个根具有正实部，故系统不稳定。

上述例子都对已确定参数的系统给出特征根，但设计或校正过程中需要进行参数的可行域分析，得借助特征方程系数稳定性判据。

3）系统稳定的必要条件

设n阶系统的特征方程

D（s）＝a0sn＋a1sn－1＋…＋an－1s＋an＝0

的n个根分别为p1，p2，…，pn，则该方程的根与系数有如下关系：

由上述方程根与系数的关系知，当系数a0＞0时（若a0＜0则特征方程两边同乘－1），欲使系统特征方程的全部根具有负实部，则必须使方程中每一个系数a0，a1，…，an全部为正，否则特征方程必将出现具有正实部或为零的根。由此得到：动态系统稳定的必要条件是系统特征方程各项系数具有相同的符号，且无一系数为零。

因此，使用稳定性判据之前可预先检查一下系统的特征方程系数，若其中有异号系数或零系数（缺项），则此系统必不稳定，不需要进一步的判定。

此条件为必要条件，存在完全满足此条件但不能确保系统稳定的情况。如某系统的特征多项式为D（s）＝（s＋2）（s2－s＋4）＝s3＋s2＋2s＋8，其系数均为正数，但系统有两个带正实部的共轭复根，系统不稳定。

［例4-04］ 如图4-9所示是液位控制系统及其函数方框图，各参数均为正数，试判断该系统的稳定性。

图4-9 液位系统及其函数方框图

［解］ 此系统的闭环特征多项式为

D（s）＝Tms3＋s2＋KpKmK1K0

此多项式中缺少s项，即一次项的系数为零，按系统稳定的必要条件知系统不稳定。这种缺项的不稳定是结构性不稳定，无法通过调整Tm、Kp、Km、K1、K0解决。