宇宙边界究竟有多大

史蒂芬·霍金

我将在第三次讲演中转向宇宙学。宇宙学在过去被认为伪科学并且是一些物理学家的保留地，供这些在早年也许做过一些有用的工作，但在晚年进入玄秘状态的人栖息。有两种原因导致这种看法。第一种是过去几乎没有任何可靠的观测。的确，直到本世纪20年代左右，仅有的重要的宇宙学观察就是夜空是黑的。但是人们并没有领会到它的意义。然而，近年来宇宙观测的范围和质量随着技术的发展而得到巨大的改善。这样，说宇宙学没有观测基础，进而反对它作为科学的说法就不再站得住脚了。

然而，还存在第二种而且更严重的反对。宇宙学除非对初始条件做了一些假设，它对宇宙不能作任何预言。没有这种假设，则人们所能说的是，事情之所以像现在这样，是因为在更早先阶段它是那种样子。而许多人相信，科学只应关心制约宇宙如何随时间演化的定域的定律。他们会觉得，确定宇宙如何启始的宇宙边界条件是形而上学或宗教的问题，而不是科学的问题。

这情形因罗杰和我证明的定理而恶化。这些定理指出，根据广义相对论，在我们的过去应该有奇性。场方程在奇性处无法定义。这样广义相对论导致了自身的失效：它预言它不能预言宇宙。

虽然许多人欢迎这个结论，我对之却极度不安。如果物理定律可以在宇宙的开端失效，为何不能在任何地方失效？在量子理论中有一条原则，只要不是被绝对禁戒的事物都是会发生的。一旦人们在路径积分中允许奇性历史参与，它们就会随时随地发生，而预见性便会消失殆尽。如果在奇性处物理学定律失效，那么在任何地方都会失效。

科学理论的唯一出路是，物理定律必须处处成立，包括宇宙的开端也不例外。人们可把这些认为是民主原则的胜利：为何宇宙的开端可以免除适合他处的定律的制约？如果所有点都是平等的，就绝不能让一些点比其他点更平等些。

为了实施物理定律在任何地方都有效的观念，人们应该让路径积分只对非奇性度规求和。人们在通常的路径情形下得知，测度更集中于不可微的路径。但是在某些合适的拓扑中，这些路径是光滑路径的完备化，并具有定义完好的作用量。类似的，人们会预料到，量子引力的路径积分应该对光滑度规的完备化空间求和。路径积分不能包括的是奇性的度规，因为它的作用量没有定义。

我们看到，在黑洞的情形中，路径积分应对欧氏也就是正定度规求和。这意味着像史瓦西解这样的黑洞的奇性在欧氏度规中不出现，欧氏度规并没有到达视界里面去。相反的，视界像是极坐标的原点。因此欧氏度规的作用量是完好定义的。人们可以把这个认为是宇宙监督的量子版本：奇性处结构的破坏不应影响任何物理测量。

因此，量子引力的路径积分看来应该对非奇性欧氏度规求和。但是对这些度规上应赋予什么样的边界条件？存在两个也只有两个自然的选择。第一个是度规在紧致集之外要趋近于平坦的欧氏度规。第二种可能性是在紧致和没有边界的流形上的度规。

量子引力路径积分的自然选取

1.渐近平坦的欧氏度规。

2.没有边界的紧致度规。

第一类渐近欧氏度规对于散射计算显然很适合（图5.1）。人们在这些度规中从无穷把粒子发进来，再在无穷观察跑出什么来。所有的观察都在无穷进行，在无穷处的背景度规是平坦的，可以以通常方式把场的小起伏解释成粒子。人们不必询问在中间的相互作用区域发生了什么。这就是为何人们让相互作用区域的路径积分对所有可能历史求和，也就是对所有渐近欧氏度规求和。

    

图5.1　在散射计算中，我们在无穷测量入射和出射粒子，因此我们要研究渐近欧氏度规。

然而，人们在宇宙学中有兴趣在有限区域而不是在无穷进行测量。我们处于宇宙之中，而非从外界来窥视宇宙。为了看到这种差异，首先让我们假定，宇宙学的路径积分是对所有渐近欧氏度规求和。那么，对于在有限区域的测量的概率存在两种贡献。第一种来自于连通的渐近欧氏度规。第二种来自于非连通的度规，它由一个包含测量区域的紧致时空和一个与之相分离的渐近欧氏度规组成（图5.2）。人们不能把非连通度规从路径积分中排除，因为它们可由连通度规来近似，在此度规中不同的部分可由具有可以忽略的作用量的细管或虫洞连接起来。

  

图5.2　宇宙测量是在有限区域进行，所以我们必须考虑两种类型的渐近欧氏度规：连通的（上）和非连通的（下）。

由于时空的非连通的紧致区域不和无穷连接，而测量却是在无穷进行的，所以紧致区域不影响散射计算。但是它们会影响宇宙学中的测量，因为它是在有限区域进行的。的确，这种非连通度规的贡献远远压倒来自连通的渐近欧氏度规的贡献。这样，人们即便把宇宙学的路径积分对所有渐近欧氏度规求和，其效应和对所有紧致度规求和几乎完全相同。因此，对宇宙学的路径积分，看来更自然的是取对所有无边界的紧致度规求和，正如哈特尔和我在1983年所提议的那样（哈特尔和霍金1983）。

无边界假设（哈特尔和霍金）

量子引力的路径积分是对所有紧致欧氏度规求和。

人们可以把它重述为“宇宙的边界条件是它没有边界。”

我在这次讲演的以下部分要指出，这个无边界假设似乎能解释我们生活于其中的宇宙。那是一个各向同性的、均匀的、具有微小微扰的膨胀宇宙。我们可以在微波背景的起伏中观察到这些微扰的谱和统计。这些结果迄今和无边界假设相一致。当微波背景的观测被延伸到更小的角度范围时，这种观察便成为无边界假设和欧氏量子引力整个学说的试金石。

为了使用无边界假设来作假设，引进能用以描述宇宙在一个时刻的状态的概念很有助益。考虑时空流形M包含一个嵌入的三维流形∑的概率，这三维流形的度规用hij来表示。它由一个对所有在M上的度规gab的路径积分来计算，在此要求度规gab在∑上的导出度规为hij。

在∑上导出度规hij的概率=∫M上在∑上导出hij的度规d[g]e-I

如果M是单连通的，这正是我要假设的，则面∑就把M分成两部分，M+和M-（图5.3）。在这种情形下，∑具有度规hij的概率是可以因式分解的。它是两个波函数Ψ+和Ψ-的乘积。它们分别是从对所有M+和M-上的度规求和的路径积分得出，而这些度规在∑上导出给定的三维度规hij。

hij的概率=Ψ+（hij）×Ψ-（hij）

此处

Ψ+（hij）=∫M+上在∑上导出hij的度规d[g]e-I

在多大数情形下，这两个波函数相等，所以我将把上标+和-去掉。Ψ被称作宇宙的波函数。如果还有物质场，则波函数还依赖于它们在∑上的值φ0。但是由于在一个闭合的宇宙中不存在一个特别优越的时间坐标，所以波函数并不显明地和时间有关。无边界假设的含义是，宇宙的波函数是由一个对在紧致流形M+上的场求和的路径积分给出，这些流形的仅有边界是表面∑（图5.4）。该路径积分是对在M+上所有度规和物质场求和，而这些度规和场在∑和hij以及物质场φ0相一致。

  

图5.3　表面∑把紧致的、单连通的流形M分割成M+和M-两部分。

   

图5.4　波函数由在M+上的一个路径积分给出。

人们可以把表面∑的位置描述成∑上的三坐标xi的函数τ。但是由路径积分定义的波函数不能依赖于τ或者坐标xi的选取。这表明波函数Ψ必须服从四个泛函微分方程。其中三个方程叫做动量约束。

动量约束方程

它们表达了这样的事实，即对于相互之间可由坐标变换得到的不同三度规hij，其波函数必须相同。第四个方程称为惠勒德威特方程。

惠勒德威特方程

它对应于波函数与τ无关。人们可以把它认为是宇宙的薛定谔方程。但是，因为波函数不显明地依赖于时间，所以没有时间导数项。

人们为了估计宇宙的波函数，正如在黑洞的情形，可以利用路径积分的鞍点近似。人们在流形M+上找到满足方程的欧氏度规g0，并要求g0在边界∑上导出度规hij。然后，人们可把作用量围绕着背景度规g0作级数展开

和前面一样，微扰线性项消失。平方项可认为是背景中的引力子的贡献，而更高阶项是引力之间的相互作用。当背景的曲率半径和普朗克尺度比较大时，这些可以不管，因此，

人们可从一个简单的例子看到波函数像什么样子。考虑一种没有物质场的情形，这儿只存在一个正的宇宙常数Λ。让我们取∑为一个三维球并且hij为半径a的标准三维球度规。然后以∑为边界的流形M+可取为四维球。满足场方程的度规是具有半径的四维球的一部分，此处。其作用量为：

对于半径比还小的三维球∑，存在两个可能的欧氏解：M+可以比半球面少或者多（图5.5）。然而，可以论证道，人们应当取对应于少于半球面的那个解。

  

图5.5　具有边界∑的两个可能的欧氏解M+，以及它们的作用量。

下一张图（图5.6）标出了度规g0的作用量对波函数的贡献。当∑的半径比小时，波函数以ea2的形式指数地增大。然而，当a比还大时，我们可以对更小半径a的结果作解析连续，而得到非常快速振荡的波函数。

   

图5.6　波函数作为∑的半径的函数。

人们可对波函数作如下解释。具有Λ项和最大对称性的爱因斯坦实时解是德西特空间。它可以被作为一个旋转双曲面被嵌入五维闵可夫斯基空间中（见方框5.A）。人们可以把它考虑成一个闭合宇宙，这个宇宙从无限尺度收缩到一个极小半径，然后又呈指数地膨胀。这个度规可以写成带有尺度因子为cosh H t的弗里德曼形式。代换τ=it把cosh变成cos给出了具有半径的四维球的欧氏度规（见方框5.B）。这样，人们得知，当波函数随三度规hij，以指数方式变化时，它就对应于虚时间欧氏度规。另一方面，波函数快速振荡对应于实时间洛氏度规。

方框5.A.洛氏德西特度规

方框5.B.欧氏度规

正如在黑洞对产生的情形，人们可以描述一个指数膨胀宇宙的自发创生。人们把欧氏四维球的下半部和洛氏旋转双曲面连接起来（图5.7）。和黑洞对产生的情形不同的是，人们不能说德西特宇宙是从一个预先存在的空间中的场能创生出来的。相反的，可以相当准确地按字面意义上说，宇宙是由无创生出来的：不仅仅是从真空出来，而根本是从绝对的无中出来，因为在宇宙之外没有任何东西。在欧氏范畴，德西特宇宙只不过是一个闭合的空间，正如地球的表面，只不过多了两维而已。如果宇宙常数比普朗克值小，欧氏四维球的曲率应该很小。这表明路径积分的鞍点近似是可靠的，而且不会因为我们忽视在非常高曲率下所发生的而影响宇宙波函数的计算。

  

图5.7　用半个欧氏解和半个洛氏解连接来描述产生膨胀宇宙的隧道效应。

人们还可以对不是完美的三维球度规的边界解场方程。如果三维球的半径比小，则解为实的欧氏度规。和具有相同体积的完美的三维球相比较，作用量是实的而且波函数呈指数式衰减。如果三维球的半径比这个临界半径大，则存在两个复共轭解，而波函数将会随hij的微小变化而快速振荡。

在宇宙中作的任何测量都可以按照波函数来表述。这样，无边界假设使宇宙学成为科学，因为人们可以预言任何观察的结果。我们刚才考虑的没有物质场只有宇宙常数的情形不对应于我们生活其中的宇宙。尽管如此，它是个有用例子，不仅因为它是一个简单的并能相当显明地解出的模型，而且我们将要看到，它对应于宇宙的早期阶段。

虽然从波函数看并不明显，但一个德西特宇宙和黑洞相当类似地具有热性。把德西特度规写成和史瓦西解相当类似的静态形式就能看到这一点（见方框5.C）。

方框5.C.德西特度规的静态形式

ds2=-（1-H2 r2）dt2+（1-H2 r2）-1 d r2+r2（dθ2+sin2θdφ2）

在处有一表观奇性。然而，正如在史瓦西解的情形，人们用坐标变换可以把它排除，而它对应于一个事件视界。这可以从卡特彭罗斯图上看到，它是一个正方形。左边的点垂直线代表球对称中心，在这儿二维球的半径r为零。另一个球对称中心由右边的点垂直线代表。在顶上和底下的水平线代表过去和将来的无穷，在这个情形下它们是类空的。从左上方到右下方的对角线是在左手对称中心的观察者过去的边界。这样，它可以称作事件视界。然而，一位世界线在未来无穷的其他地方终结的观察者具有不同的事件视界。这样，在德西特空间中事件视界是个人的事物。

如果人们回到德西特度规的静态形式，并且令τ=it便得到欧氏度规。在视界上有一表观奇性。然而，只要定义一个新的径向坐标并且在τ坐标以周期来等同，就得到一个规则的欧氏度规，它刚好是四维球。因为虚时间坐标是周期性的，所以德西特空间和在它之上的所有量子场的行为就好像它们具有温度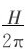似的。正如我们将要看到的，我们在微波背景的起伏中可以观察到这个温度的后果。人们还可以像处理黑洞那样，对欧氏德西特解的作用量进行论证。他会发现它具有内禀熵，这正是事件视界面积的四分之一。这个熵又是因拓扑原因引起的：四维球的欧拉数为二。这表明在欧氏德西特空间中不可能有全局时间坐标。人们可以把这一宇宙熵解释成观察者对在他的事件视界之外的宇宙知识的缺失。

具有周期的欧氏度规

德西特空间不是我们生活于其中的宇宙的好模型，因为它是空的而且在呈指数地膨胀。我们观察到宇宙包含物质，而且我们从微波背景和轻元素丰度推出，它在过去必须更热更密得多。和我们观察一致的最简单的方案便是所谓的“热大爆炸”模型（图5.8）。在这个场景中，宇宙在充满具有无限温度的辐射的一个奇性启始。随着它的膨胀，辐射冷却而且能量密度降低。最后，辐射的能量密度比非相对性物质的密度还低，而膨胀变成物质占主导的了。然而，我们仍然可以在微波辐射的背景中看到辐射的残余，它具有大约比绝对零度高3K的温度。

   

图5.8　在热大爆炸模型中宇宙半径和温度作为时间的函数。

热大爆炸模型的麻烦正是所有宇宙学的麻烦，它没有初始条件的理论：它没有预言能力。因为广义相对论在奇性处失效，从大爆炸可以冒出任何东西来。这样，为何宇宙在大范围内是如此地均匀和各向同性，却还有诸如星系和恒星这样的局部无规性呢，为何宇宙是如此接近于重新坍缩和无限膨胀之间的分界线呢？为了使它像现状这么接近，早期的膨胀率必须不可思议地精确选定。如果在大爆炸后1秒其膨胀率小了10-10，则宇宙在几百万年之后就应坍缩。如果它大了10-10，宇宙就会在几百万年之后基本上是空的。在任何情形下都不会有足够时间让生命得以发展。这样，人们要么必须求助于人存原理，要么必须寻找物理学的解释，说明宇宙为何是这种样子的。

热大爆炸模型不能解释为何：

1.宇宙几乎是均匀和各向同性的，但是却具有小微扰。

2.宇宙在以几乎刚好避免重新坍缩的临界率膨胀。

有些人宣布，所谓的暴涨能够使初始条件理论成为多余。其思想是宇宙在大爆炸时可以从几乎任意状态启始。在宇宙中具有合适条件的部分会出现叫做暴涨的指数膨胀时期。这个不仅使该区域尺度增加一个巨大的达到1030或更多的倍数，并且还使该区域既均匀又各向同性，还使它以刚好避免再坍缩的临界速率膨胀。他们还声称只有在暴涨区域智慧生命才得以发展。因此，对我们的区域如此之均匀以及各向同性，还刚好以临界速率膨胀，不应感到惊讶。

然而，光用暴涨不能解释宇宙的现状。人们要看到这一点很容易，只要取现在宇宙的任何态并让它向时间的过去演化。假定它包含足够物质，则奇性定理表明，在过去存在有奇性。人们可以在大爆炸选取这个模型的初始条件作为宇宙初始条件。人们以这种方法可以指出，大爆炸处的任意初始条件能导致现在的任何状态。人们甚至不能争辩道大多数初始条件会导致像我们今天观察到的状态：无论是导致像还是不像我们宇宙的初始条件的自然测度都是无限的。所以人们不能断言何者测度更大些。

另一方面，我们看到在具有宇宙常数但没有物质场的引力情形，无边界条件会导致一个在量子理论极限内可被预言的宇宙。这个特殊的模型并不描述我们生活于其中的宇宙，我们的宇宙充满了物质而且具有零值或者非常小的宇宙常数。然而，人们可以抛弃宇宙常数并包括进物质场以得到一个更现实的模型。尤其是似乎需要一个具有势V（φ）的标量场φ。我将假定V在φ=0时有一为零的极小值。简单的例子便是具有势V=的有质标量场（图5.9）。

标量场的能动量张量

人们从能动量张量可以看到，如果φ的梯度很小，则V（φ）就像一个有效宇宙常数那样起作用。

现在波函数不仅依赖于导出度规hij，而且依赖于φ在∑上的值φ0。对于小的三维圆球面以及大的φ0值，人们可以解场方程。具有这种边界的解近似地为四维球的一部分，以及几乎为常数的φ场。这就像德西特情形，而势V（φ0）起着宇宙常数的作用。类似的，如果三维球的半径a比欧氏四维球的半径还大，将存在一对复共轭解。这些就像半个欧氏四维球连接到洛氏德西特解上去，而标量场φ几乎保持常数。这样，无边界假设不仅在德西特情形而且在这个模型中，预言了一个指数膨胀宇宙的自发创生。

   

图5.9　有质标量场的势。

现在人们可以考察这个模型的演化。和德西特情形不同，它不继续无限地呈指数膨胀下去。标量场将从势V的山上滚下来到达它极小值即φ=0处。然而，如果φ的初始值比普朗克值更大，则滚下的速率就比膨胀的时间尺度更慢。当标量场降低到一的数量级，它就开始在φ=0附近振荡。对于大多数势V，这种振荡比膨胀时间快。人们通常假定，这些标量场振荡的能量会转变成其他粒子对，并把宇宙加热上去。然而，这一些要依时间箭头的假设而定。我会很快地回到这一点上来。宇宙在经历了巨大倍数的指数膨胀之后就具有几乎恰好的临界膨胀率。这样，无边界假设就能解释，为何现在宇宙仍然这么接近于临界膨胀率。为了研究它对宇宙均匀性和各向同性的预言，人们必须考虑对完美的三维球度规微扰的三度规hij。人们可以把它按照球谐函数展开。它们共有三类：标量谐波，矢量谐波以及张量谐波。而矢量谐波只不过对应于连续的三维球上的坐标x i的改变，并不起任何动力学作用。张量谐波对应于在膨胀宇宙中的引力波，而标量谐波一部分对应于坐标自由度，另一部分对应于密度微扰。

张量谐波——引力波

矢量谐波——规范

标量谐波——密度微扰

人们可以把波函数表成半径为a的完美三维球的度规的波函数乘上各谐波系数的波函数的乘积：

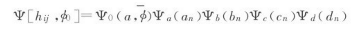
然后人们把波函数的惠勒德威特方程按半径a和平均标量场φ展开到无穷多阶，但是按照微扰只展开到第一阶。人们就得到一系列相对于背景度规的时间坐标的微扰改变率的波函数要满足的薛定谔方程。

薛定谔方程

等等。

人们可以利用无边界条件去获得这些微扰波函数的初始条件。人们对一个小的但是稍微变形的三维球解场方程。这就得到在指数膨胀时期的微扰波函数。然后可以利用薛定谔方程去演化之。

对应于引力波的张量谐波考虑起来最为简单。它们不具有任何规范自由度而且和物质微扰不直接相互作用。人们可以利用无边界条件在被微扰的度规中去解张量谐波的系数dn的初始波函数。

基态

人们发现，它正是一个谐振子在引力波频率下的基态波函数。该频率随宇宙膨胀而下降。当频率比膨胀率a/a更大时，薛定谔方程允许波函数绝热地松弛而该模式将停留在它的基态。然而，频率最终会变得小于膨胀率，膨胀率在指数膨胀期间大体为常数。当频率变得比膨胀率更小时，薛定谔方程不再能足够快地改变波函数，使得它在频率改变时仍然维持在基态，相反的，它将把原先的波函数形状凝固。

在指数膨胀时期之后，膨胀率比模式的频率下降得更快。这等效于说，观察者事件视界，也就是膨胀率的倒数比模式的波长增大得更快。这样，波长将会在暴涨期间变得比视界还长，而且后来义会回到视界之内（图5.10）。到这一时刻，波函数仍然和波函数凝固时一样。然而，其频率是低得多了。因此波函数对应于高度激发态，而不是波函数凝固时的基态。引力波模式的这些量子激发产生微波背景的角度起伏，其幅度是波函数凝固时（在普朗克单位）的膨胀率。这样，宇宙背景探索者在微波背景上观测到10-5的起伏，为在波函数凝固之时的能量密度设下了大约10-10普朗克单位的上限。这个值低到足以保证我用过的近似十分准确。

   

图5.10　在暴涨中波长和视界半径是时间的函数。

然而，引力波张量谐波只为凝固时间的密度立下上限。其缘由是，标量谐波引起微波背景的更大起伏。在三度规hij中有两个标量谐波自由度，在标量场中有一个。然而，其中的两个对应于坐标自由度。这样，只存在一个物理的标量自由度，而它对应于密度微扰。

如果人们对直至波函数凝固之前和之后各选取一个坐标，则可以对标量谐波采取和对张量谐波非常类似的分析方法。在从一个坐标向另一坐标系统变换之中，其幅度被放大的因子是膨胀率除以φ的平均变化率。这个因子依赖于势的斜率，但是对于合理的势至少为十。这表明密度微扰产生的微波背景起伏起码比引力波产生的大十倍。这样在波函数凝固时刻的能量密度的上限只有普朗克密度的10-12。这就很安全地处于我使用过的近似的有效范围之内。这样看来，甚至对于宇宙的开初我们也不需要弦理论。

随角度大小的起伏的谱，在当前观测的精度内和几乎与张角无关的预言相符。而密度微扰的大小刚好是需要来解释星系和恒星的形成。这样看来，无边界假设能解释宇宙的所有结构，包括像我们这样的微小的非均匀性。

宇宙背景探索者预言=＞能量密度上限

加上引力波微扰　10-10普朗克密度

加上密度微扰=＞能量密度上限

10-12普朗克密度

早期宇宙内在引力温度≈10-6普朗克温度=1026度

人们可以认为微波背景的微扰是由标量场φ的热起伏引起的。暴涨时期具有膨胀率除以2π的温度，因为它在虚时间方向近似地呈周期性。这样，在某种意义上，我们不需要寻找微小的太初黑洞：我们已经观测到大约1026度的，或者10-6倍的普朗克温度的内禀引力温度。

关于和宇宙事件视界相关的内禀熵能说些什么呢？我们能观察到这个吗？我想我们能，而且我认为它对应于这个事实，即像星系和恒星这样的物体是经典物体，尽管它们是由量子起伏形成的。如果人们在一个类空表面∑看宇宙，这个表面在某一时刻横贯整个宇宙，则宇宙处于由波函数Ψ描写的单独的量子态中。然而，我们永远看不到比∑的一半更多，而且我们对于在我们过去光锥之外的宇宙是什么模样完全无知。这意味着在计算观察的概率之时，我们必须把∑上我们不能观测到的部分的所有可能性求和（图5.11）。求和的效应是把我们观测的宇宙的部分从一个单独量子态改变成所谓的混合态，即不同可能性的统计系统。如果一个系统具有经典的而非量子的方式行为，这种所谓的离析是必须的。人们通常把离析归因于与诸如热库的不被测量的外界系统相互作用。在宇宙的情形中不存在外界系统，但是我提议，我们观察到经典行为的原因是因为我们只能看到宇宙的部分。人们也许会认为，在以后的时刻他能看到全部宇宙而且事件视界会消失。但是事情并非如此。无边界假设表明宇宙是在空间上闭合的。一个闭合宇宙将会在观察者看到整个宇宙之前重新坍缩。我曾经尝试证明，这样一个宇宙的熵在它最大膨胀时刻应为其事件视界面积的1/4（图5.12）。然而，我在此刻似乎得到3/16的因子，而不是1/4。很明显，我要么弄错了，要么丢掉什么了。

   

图5.11　一位观察者只能看到任何表面∑的部分。

    

图5.12　在观察者能看到整个宇宙之前，它就坍缩到最后的奇性。

我要在罗杰和我意见非常分歧的一个论题上结束这次讲演——时间箭头。在宇宙的我们区域中在向前和向后方向存在非常清楚的区别。人们只要把影片往回倒即能看到这个差别。杯子不是从桌沿落下并粉碎，而是碎片自己拼补好并跳回到桌子上。如果真实生活都像这样就好了。

物理场服从的局部定律是时间对称的，或者更精确点说，是CPT不变的。这样，在过去和将来之间观察到的差别应该来自于宇宙的边界条件。让我们接受宇宙是在空间上闭合的，而且它膨胀到最大尺度然后再坍缩。正如罗杰强调的，在这个历史的两端宇宙是非常不同的。在我们叫做宇宙开端的，似乎曾经非常光滑而且规则。然而，我们预料当它重新坍缩时，会变成非常无序和无规，因为存在比有序的配置多得太多的无序的配置，这表明初始条件曾经被不可思议地精密地选定过的。

因此，似乎在时间的两端必须有不同的边界条件。罗杰的设想是，在时间的一端而不是另一端外尔张量必须为零。外尔张量是时空曲率中不由物质通过爱因斯坦方程定域决定的那部分。它在光滑的有序的早期阶段曾经很小，但是在坍缩的宇宙中很大。这样这个假设把时间的两端区分开来并因此可以解释时间的箭头（图5.13）。

   

图5.13　用外尔张量假设来区别宇宙的两端。

我以为罗杰的假设中的外尔张量是在不止一层含义上来说的。首先，它不是CPT不变的。罗杰把这当作优点，而我却觉得除非有不得已的理由去抛弃对称，我们应当坚持之。正如我要论证的，不必要放弃CPT。其次，如果在早期宇宙外尔张量一度准确地为零，那时宇宙就应是完全均匀且各向同性的而且会在所有的时刻保持如此。罗杰的外尔假设既不能解释背景中的起伏，也不能解释产生星系以及像我们身体这样的微扰。

对外尔张量假设的异议

1.不是CPT不变的。

2.外尔张量不能一度准确为零。不能解释小起伏。

尽管这一切，我以为罗杰抓住了时间两端的一个重要差别。但是外尔张量在一端很小的事实不能被当作一个特别的边界条件而应从一个更基本的原则，即无边界假设推出。正如我们已经看到的，这意味着在围绕着半个欧氏四维球和半个洛氏德西特解相接的背景的微扰处于它们的基态。那就是说，它们是和不确定原理相一致的尽量小的状态。这个就隐含着罗杰外尔张量条件：外尔张量不是精确地为零，它是尽可能地接近于零。

我起先认为：这些有关微扰处于它们基态的论证可适用于膨胀收缩循环的两端。宇宙从光滑和有序启始，而随着膨胀变得更无序和无规。然而，我以为当它变小时又必须回到一种光滑和有序的状态。这就意味着在收缩相热力学时间箭头要反向。杯子又会自己拼凑好并跳到桌子上来。随着宇宙重新缩小，人们越活越年轻，而不是越活越老。由于等待宇宙重新坍缩需要太长时间，所以等到那时返回青春是无望的。但是如果当宇宙收缩时，时间箭头反向，那么在黑洞之内也应反向。可是，我不想提倡将跳进一个黑洞作为一个人延年益寿的好办法。

我写了一篇文章宣称，当宇宙重新收缩时，时间箭头会反向。但是之后和当·佩奇以及雷蒙·拉弗勒蒙的一番讨论使我信服，我犯了最大的错误，或者是我在物理学上的最大错误：宇宙不在坍缩中回到光滑的状态。这表明时间箭头并不反向。它会继续像在膨胀相中一样指向相同方向。

时间的两个端点何以这么不同呢？为何在一端微扰必须很小，而另一端却不？其原因是，场方程存在配合微小三维球边界的二个可能的复数解。一个正是我早先描述过的：它是近似地用半个欧氏四维球和洛氏德西特解的一个小部分相连接（图5.14）。另一种可能解是以同样的半欧氏四维球连接到一个洛氏解上，该洛氏解膨胀到非常大的半径，然后再收缩到给定边界的小半径（图5.15）。很显然，一个解对应于时间的一端，而另一个解对应于另端。这两个端点之间的差别来自于这个事实，在第一个仅具有很短的洛氏时期的解的情形，三度规hij的微扰衰减得很厉害。然而，在膨胀又收缩的解的情形，微扰可以非常大并不被显著地衰减。这就引起了罗杰指出的时间两端之间的差别。宇宙在一端非常光滑并且外尔张量非常小。然而，它不能准确地为零，因为那样会违反不确定性原理。相反的，存在很小的起伏，这些起伏后来成长为星系以及像我们这样的身体。与此成鲜明对比的是，在时间的另一端点，宇宙会非常无规而且混沌，外尔张量极其巨大。这就解释了观察到的时间箭头以及为何杯子从桌子滑落粉碎而非拼凑好再跳上来。

   

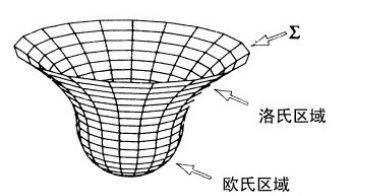
图5.14　半个欧氏四维球连接到一个小的洛氏区域。

由于时间箭头不准备反向——而我已经超过时间——我最好结束讲演。我强调了我在时空研究中获悉的自认为两个最显著的特点：（1）引力弯曲时空，使它有一个开端和一个终结；（2）因为引力本身确定它作用其上的流形的拓扑，这就导致在引力和热力学之间存在一个深刻的关联。

时空正曲率产生奇性，经典广义相对论在奇性处失效。宇宙监督可以为我们防御黑洞的奇性，但是大爆炸奇性赤裸裸地暴露在我们面前。经典广义相对论不能预言宇宙如何开端。然而，量子广义相对论和无边界假设一道，预言了我们观察到的宇宙，而且甚至似乎预言了在微波背景中观察到的起伏的谱。然而，虽然量子理论恢复了经典理论丧失了的预言性，但它并没有完全做到。因为存在黑洞和宇宙事件视界，我们不能看到整个时空，我们观察由量子态的系综而不是一个单独的态描述。这就引进了额外水平的不可预见性，但它也还可能是使宇宙看起来是经典的原因。这也许能把薛定谔猫于半死半活之间拯救出来。

    

图5.15　半个欧氏四维球连接到一个小的洛氏区域，该区域膨胀到最大半径然后重新收缩。

从物理学中把可预见性取消，然后在一种减少的程度上又把它恢复，这是一桩相当成功的故事。我的话完了。