婆罗摩笈多—婆什迦罗法则

5世纪至12世纪，是印度数学发展的鼎盛时期。这一时期最有代表性的印度数学家，除阿耶波多外，还有婆罗摩笈多、马哈维拉、婆什迦罗。在上面我们已经介绍了阿耶波多，在这一章我们简单介绍一下婆罗摩笈多与婆什迦罗。

婆罗摩笈多（约598～670），古印度最著名的数学家、天文学家之一。

大约在598年，婆罗摩笈多出生于印度北部。后来他一生的大部分研究生涯都在当时印度数学、天文学活动中心之一的乌贾因度过。628年，大约30岁的婆罗摩笈多完成了其主要著作《婆罗摩修正体系》。这本书也是以当时印度最传统、最常见的诗体形式编排的。全书共24章，大多数章节是关于天文学研究的，但在其中涉及数学知识。专论数学的有两章（第12章“算术”与第18章“代数”）。

婆罗摩笈多的这一著作问世后，许多学者对其进行过研究。8世纪时，婆罗摩笈多的这本著作又被带到巴格达，在皇室的支持下译成阿拉伯文，对当时阿拉伯的天文学和数学产生了很大影响。比如印度的十进制记数法就是通过此书而被阿拉伯世界所了解并接受的，而且据传花拉子密的《代数学》一书也是根据婆罗摩笈多的著作写成的。

在这本著作中，婆罗摩笈多作出了许多重要数学贡献，其中许多在世界数学史上有较高的地位。如：比较完整地叙述了零的运算法则；在印度最早认识负数概念，用负数表示欠债，提出了负数的四则运算法则，其中负数的乘除法则是历史上第一次提出；给出二次方程的求根公式；在数学符号方面，用不同颜色名称的头一个音节表示未知数……在三角学与几何学，特别是不定方程方面婆罗摩笈多也有令人瞩目的发现。

在不定方程方面，婆罗摩笈多对阿耶波多研究过的一次不定方程ax±by=c做了进一步探讨，并将结果推广到联立不定方程及多个未知量的情形。但他更突出的贡献是他在历史上最早研究了佩尔方程，并得到许多结果。有意思的是，为了表示解这类方程在他心目中的重要，他曾向他同时代的人提出挑战，让他们找出方程92x2+1=y2的最小整数解。他声称，只能那些能在一年之内解决这个问题的人才有资格称为数学家。

现在一般认为，对佩尔方程的研究是婆罗摩笈多在数学上取得的最重要成就。下面，我们就以他提出的挑战问题为例来介绍一下他这方面所做的工作。

求解婆罗摩笈多方程：92x2+1=y2。婆罗摩笈多的解法如下：

第一步，先求解一个与所求方程相关的，但更易求解的不定方程92x2+b0=y2，设这一新方程的解为（x0，y0）。显然，可选取b0=8，即92x2+8=y2，而这一新方程有一个非常显然的特解：x0=1，y0=10。

第二步，求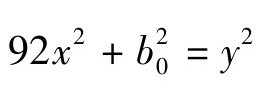即92x2+64=y2的一个特解。为此，需要借助于最早由婆罗摩笈多发现的一个命题。

命题1　如果α、β是方程Nx2+k=y2的解，且α′、β′是方程Nx2+k′=y2的解。那么x=αβ′+α′β，y=Nαα′+ββ′是新方程Nx2+kk′=y2的解。

这一结果被称为婆罗摩笈多引理。在18世纪，这一结果又被欧拉（1764）、拉格朗日（1765）重新发现。下面考虑这一引理的一种特殊情况：若α、β是方程Nx2+k=y2的解，那么x=2αβ，y=Nα2+β2是Nx2+k2=y2的解，这一结论称为婆罗摩笈多推论。把婆罗摩笈多推论应用于上面的具体例子。

因为x0=1，y0=10是92x2+8=y2的一个解，于是可得到92x2+64=y2的一个特解2x0y0=2·1·10=20，。

第三步，因为（20，192）是92x2+64=y2的一个特解，即92（20）2+82=1922。方程两边同除以82，于是得到92（20/8）2+12=（192/8）2，这一式子意味着（20/8=5/2，192/8=24）是方程92x2+1=y2的一个解。

事实上，一般的有如下命题。

命题2　如果α、β是方程Nx2±k2=y2的解，则（α/k，β/k）是Nx2±1=y2的解。

然而，由此得到的解并不一定是整数解，因此可能不满足我们的要求。如上面得到的解中的5/2不是整数。

第四步，由（5/2，24）是方程92x2+1=y2的一个解，可得（5，48）是方程92x2+4=y2的一个解。为了进而找到92x2+1=y2的一个整数解，需要借助婆罗摩笈多的另一个命题。

命题3　如果α、β是方程Nx2+4=y2的解，则x=1/2αβ，y=1/2（β2-2）是Nx2+1=y2的解。

应用这一命题，我们最终得到婆罗摩笈多方程的求解结果：

x=1/2·5·48=120，y=1/2（482-2）=1151是92x2+1=y2的一个特解。

在介绍了婆罗摩笈多关于特殊方程92x2+1=y2的求解之后，下面我们再对他的解题思路作一总结与补充。

第一步，选择适当的整数k，并得到Nx2+k=y2的一个特解（α，β）。第二步，利用命题1的结论，得到Nx2+k2=y2的一个特解（2αβ，Nα2+β2）。第三步，利用命题2的结论，得到Nx2

+1=y2的一个解。

最好的情况，至此得到的解中的值都已是整数，则原方程Nx2+1=y2的整数解已直接求得，而且这种求解过程具有一般性。对任何佩尔方程都适用。但问题是，如果解中的值不都是整数，怎么处理？

对此，婆罗摩笈多得到了部分结果。他指出，如果Nx2±2=y2，或Nx2±4=y2这两种形式的方程有整数解，那么一定可以找到Nx2±1=y2的整数解。

若k=2，Nx2+k=y2的一个特解为（α，β），那么应用上面的结论，Nx2+1=y2的一个解为。注意，因为此时，恰都为整数。这表明，只要找到Nx2+2=y2的一个特解（α，β），那么我们马上就可以得到Nx2+1=y2的一个特解（αβ，β2-1）。

若k=-2，情况与上面完全类似。

若k=4，Nx2+4=y2的一个整数解为（α，β），那么应用上面的结论，Nx2+1=y2的一个解为。

此时。

首先，注意到（α，β）若是Nx2+4=y2的一组整数解，则α，β同为偶数或同为奇数。因此，我们只需针对β的奇偶性做出讨论。

若β为偶数，那么x, y恰都为整数，于是x=1/2αβ，y=1/2（β2-2）已是Nx2+1=y2的解。上面所举的婆罗摩笈多方程正属于这种情况。

若β为奇数，则x, y都不是整数，对此可做如下处理：因为（α，β）是Nx2+4=y2的一个特解，那么是Nx2+1=y2的一个特解。又已是Nx2+1=y2的一个特解，于是应用婆罗摩笈多引理，可得：

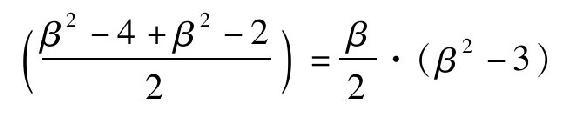也是Nx2+1=y2的解。因为β为奇数，易知此时的x, y恰都为整数。这一结果是上述婆罗摩笈多命题3的补充。

k=-4时的讨论与上面基本类似，但过程要更为复杂一些。

设Nx2-4=y2的一个整数解为（α，β），那么应用上面的结论，Nx2+1=y2的一个解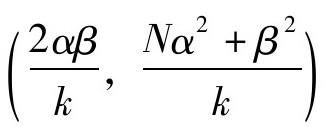。此时。显然，这一解中的x也可换作αβ/2。

首先，注意到（α，β）若是Nx2-4=y2的一组整数解，则α，β同为偶数或同为奇数。因此，我们只须针对β的奇偶性做出讨论。

若β为偶数，那么x, y恰都为整数，于是x=-1/2αβ，y=1/2（β2+2）已是Nx2+1=y2的解。若β为奇数，则x, y都不是整数，我们做如下处理：因为（α，β）是Nx2-4=y2的一个特解，那么（α/2，β/2）是Nx2-1=y2的一个特解。又x=1/2αβ，y=1/2（β2+2）也是Nx2+1=y2的根，应用婆罗摩笈多引理，可得：

也是Nx2-1=y2的解。为了得到

Nx2+1=y2的解，对此结果再应用一次婆罗摩笈多引理，并以整理则可得到：

是Nx2+1=y2的解。由β为奇数，易知此时的x, y恰都为整数。

于是，我们得到了婆罗摩笈多关于佩尔方程研究的命题4：如果α、β是方程Nx2-4=y2的解，则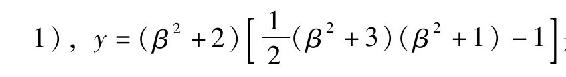是Nx2+1=y2的解。

应用婆罗摩笈多给出的以上结论，确实可以容易的解决一些佩尔方程。我们举几个例子。

例：求17x2+1=y2的一个整数解。

解：易知（1，4）是17x2-1=y2的一个整数解。对此结果应用婆罗摩笈多引理，于是可得x=2·1·4=8，y=17·（1）2+（4）2=33即（8，33）为17x2+1=y2的一个整数解。

例：求104x2+1=y2的一个整数解。

解：易知，（1，10）是104x2-4=y2的一个整数解。10为偶数，于是可以应用“x=-1/2αβ，y=1/2（β2+2）是Nx2+1=y2的解”的结果，得到它的一个整数解（-5，51）或取（5，51）。

例：求21x2+1=y2的一个整数解。

解：易知，（1，5）是21x2+4=y2的一个整数解。5为奇数，于是可应用上面命题3的补充结论得到，是21x2+1=y2

通过上面介绍，我们对婆罗摩笈多解决佩尔方程的方法及得到的结果已经有了比较清楚的了解：为了求解Nx2+1=y2，先找到一个与原方程相联系的方程Nx2+k=y2，后者的一个特解可以直接求得。然后，婆罗摩笈多介绍了如何在Nx2+k=y2的一个特解基础上，推算出原方程Nx2+1=y2的一个特解。特别是，当k=-1，±2，±4时，婆罗摩笈多给出了完整而有效的解的结论。此外，在得到一个特解后，运用婆罗摩笈多引理，反复迭代还可以得到Nx2+1=y2的无穷多组整数解。

婆罗摩笈多通过自己的四个命题（顺便指出，婆罗摩笈多原著关于这四个命题的表述是很隐晦的，我们上面所介绍的是经后人特别是20世纪30年代印度数学史家达生解释后的表述）求解佩尔方程的特殊解法，后来在印度被称为“瓦格布拉蒂”。考虑到婆罗摩笈多生活的年代，考虑到他是历史上第一个认真研究佩尔方程的人，因此他所得到的这一成就（一般认为这是他最重要的数学贡献）足以在数学史上占有一席之地。

通过上面的例子与说明，我们也看到运用他的方法确实可以非常巧妙并较容易地解决一些佩尔方程。不过，这种方法仍有较大的局限性，问题在于应用它并不能解决任意的Nx2+1=y2。比如说求解61x2+1=y2，易知61x2+3=y2有解（1，8），然而此处k=3，婆罗摩笈多的方法失效了。简单说，婆罗摩笈多并没有得到计算任意佩尔方程解的完整方法。约500年后，另一位古印度伟大数学家婆什迦罗提出另外两条命题，对婆罗摩笈多的结果作出重要补充并最终圆满地解决了这一问题。

婆什迦罗（1114～约1185），古印度最伟大的数学家和天文学家。

1114年，婆什迦罗出生在印度南部比德尔，也称婆什迦罗第二，以区别于在他之前另一位同名的数学家。成年后他长期在古印度文化中心乌贾因工作，曾担任乌贾因天文台的主持人，被认为是婆罗摩笈多的继承者。婆什迦罗的数学工作体现在他的两本代表古印度数学最高水平的著作《莉拉沃蒂》（也译《丽罗娃提》）和《算法本源》中。

关于《莉拉沃蒂》一书的书名，有一个美丽的故事。莉拉沃蒂是婆什迦罗女儿的名字，该词在印度语中原为“美丽”之意。有占星家预言她终身不能结婚。于是也是占星家的婆什迦罗另为女儿预占吉日。他把一个底部有孔的杯子放入水中，让水从小孔中慢慢渗入。杯子沉没之时，也就是女儿的吉日来临之际。女儿带着好奇观看这只待沉的杯子，不成想她颈项上的一颗珍珠不慎掉入杯中，正好堵塞了漏水的小孔，杯子停止了下沉，这就注定了她永远不能出嫁。婆什迦罗为了安慰女儿，便把自己所写的算书以她的名字命名，以使其流芳百世。该书后来被莫卧儿帝国的斐济译成波斯文。这个传说即来源于斐济的记载。

《莉拉沃蒂》共有13章，从一个信徒向神祈祷开始展开全书。第1章给出算学中的名词术语；第2章是关于整数、分数的运算，包括开平方、开立方等；第3章介绍算术中的一些计算法则和技巧；第4章是关于利率等方面的应用题；第5章涉及数列（主要是等差数列和等比数列）的计算问题；第6章介绍平面图形的度量计算；第7章至第10章是关于立体几何的度量计算；第11章为测量问题；第12章是代数问题，包括不定方程；第13章是一些组合问题。

《算法本源》共有8章，内容主要是关于算术与代数的。第1章讲述正负数法则；第2、第3章讲整系数一次和二次不定方程的解法；第4章讲线性方程组；第5章研究二次方程，并给出勾股定理的两个证明；第6章包含一些线性不定方程组的实例；第7、第8章补充了二次不定方程的内容。

可以说，婆什迦罗的著作全面而系统地介绍了算术、代数、几何、三角知识，全面发展了自阿耶波多以来印度数学的各项成果，其中许多在数学史上很有价值。如在《算法本源》第1章第3节中对零的运算法则给出了完整的论述；讨论了负数，并用“负债”或“损失”解释负数；认识并广泛使用无理数；在代数方程方面，婆什迦罗对一次特别是二次方程做了详尽的讨论，给出了完善的求解法则，并对二次方程根的性质有清楚认识；印度人对代数学的一大贡献是采用缩写文字和符号来表示未知数和运算，婆什迦罗的这两本书堪称这方面的代表作；给出毕达哥拉斯定理的两个漂亮证明，其中一个与中国数学家赵爽的方法相同，另一个在17世纪被英国数学家沃利斯重新发现；在传统的印度三角学方面，他已熟练地掌握了三角函数的和差与半角等公式；在排列组合方面他做了先驱性研究。

除此外，婆什迦罗还在印度传统的不定方程方面做出了一些前人未及的推进工作。比如，他改进、推广了库塔卡法则，处理了含有三个未知数的一次不定方程。然而，他最有独创性的工作则是他对婆罗摩笈多关于佩尔方程解法的改进，改进后的方法称为“循环过程”。

下面，我们就来介绍一下婆什迦罗关于佩尔方程的改进结果。

通过上面的介绍，我们已经知道，按照婆罗摩笈多的方法，当k=-1，±2，±4时，总可以由Nx2+k=y2的一个整数解得到Nx2+1=y2的一个整数解。婆罗摩笈多对此的阐述是完整而有效的。但问题是，如果k不属于这几类情况时，如何由Nx2+k=y2的一个整数解得到Nx2+1=y2的一个整数解呢？婆什迦罗的重要改进正是针对于此。

在找到方程Nx2+k=y2的一个解（α、β）后，婆什迦罗的做法是，另外再找一个整数m，使得（1，m）是Nx2+（m2-N）=y2的一组特解。

于是利用婆罗摩笈多引理，可知x=αm+β，y=Nα+βm是Nx2+k（m2-N）=y2的一个特解。这意味着：N（αm+β）2+k（m2-N）=（Nα+βm）2，

两边同除以k2，有

根据“库塔卡法”可以找到m，使αm+β可被k整除，并使m2-N的绝对值取最小值。而且可以证明：若αm+β可被m整除，那么m2-N与Nα+βm也都可被m整除。这正是婆什迦罗得到的命题1。

接受这一命题的结果，于是可设，，这样就得到一个新的结果：，其中α1，k1，β1都是整数。

重复上面的过程，可得到另一个新方程：，其中α2，k2，β2都是整数。

这样的操作可以一直重复进行下去。婆什迦罗给出的第二个命题指出，在经过有限次这种操作后，一定可以得到如下形式的结果：Na2+k=b2，其中a, b为整数，而k=±1，或±2，或±4。走到这一步，再利用婆罗摩笈多的方法，就总可以得到Nx2+1=y2的一个解了。

为了说明自己的结果，婆什迦罗在他的著作中给出5个这种类型的方程以及它们的解答，这5个方程分别是8x2+1=y2、11x2+1=y2、32x2+1=y2、67x2+1=y2、61x2+1=y2。

下面我们就用婆什迦罗的方法求解一下比较复杂的61x2+1=y2。

解：首先易知61x2+3=y2有解（1，8）。下面要选择m，使αm+β=m+8可被3整除，并使|m2-N|=|m2-61|足够小。不难发现，可取m=7。此时，。这样，在经过一次婆什迦罗给出的操作后，我们就得到了：61x2-4=y2的一个特解（5，39）。

下面再利用婆罗摩笈多的命题4即可求得原方程61x2+1=y2的一个解：

我们再举一个更复杂的例子，求解97x2+1=y2。

解：首先易知97x2+3=y2有解（1，10）。下面要选择m，使αm+β=m+10可被3整除，并使|m2-N|=|m2-97|最小。不难验算，可取m=11。此时，。

这样，在经过一次婆什迦罗给出的操作后，我们得到了新方程97x2+8=y2的一个特解（7，69）。但k1=8，所以要重复上面的操作。

为此要选择m1，使7m1+69可被8整除，并使最小。经验算，可取m1=13。此时，。

这样，在经过第二次婆什迦罗给出的操作后，我们得到新方程97x2+9=y2的一个特解（20，197）。但k2=9，所以还要重复上面的操作。

继续下去，在经过第三次操作后，可以得到新方程97x2+11=y2的一个特解（53，522）。经过第四次操作后，可以得到新方程97x2-3=y2的一个特解（86，847）。经过第五次操作后，可以得到新方程97x2-1=y2的一个特解（569，5604）。至此k=-1，化为了婆罗摩笈多已解决的结果。最后利用婆罗摩笈多的结论，可最终得到97x2+1=y2的一个特解（6377352，62809633）。

过程非常烦琐，但利用婆什迦罗改进后的方法并结合婆罗摩笈多的工作，问题确实得到了解决。现在，由婆罗摩笈多开创并由婆什迦罗做出重要补充的这种求解佩尔方程的一般性解法被称为婆罗摩笈多—婆什迦罗法则，它得到许多数学史家的高度评价，被看做是古印度数学最突出的成就。

不过，与婆罗摩笈多一样，婆什迦罗对自己的两个命题没有证明。实际上，对古印度人来说，他们与古中国人一样，重视的是具体应用。即找到一般算法，并用其解决具体问题。

上面介绍了婆罗摩笈多与婆什迦罗的方法。下面我们再来介绍一种后来被普遍使用的方法：连分数法。

在介绍二元一次不定方程的解法时我们已经介绍过连分数法。但在那里，我们所遇到的是把有理数表示成连分数。事实上，任何实数都可写成一个简单连分数。具体而言，有理数一定可表示成有限连分数，即其连分数的形式中元素的个数必定是有限个；而无理数则一定可表示成无限连分数，即其连分数的形式中元素的个数必定是无限个。那么，如何把任意一个无理数x表示为无限连分数呢？思路是简单的。方法是：先取出这一无理数的整数部分a1，设剩下的小数部分为r1，于是，而1/r1>1。对1/r1进行同样的操作，即取出其整数部分，设为a2，而其小数部分为r2，于是，而1/r2>1……这个运算过程永无止境，它将形成一个无限连分数。简单而言，要执行的算法基本上只有两条：取出商数中的整数部分；将商的小数部分颠倒。如此反复地进行下去。

因为我们这里的探讨将只涉及√N一类无理数，因此下面我们只研究不尽根式√N的连分数表示。对此，首创连分数近代理论的意大利数学家邦贝利在其专著《代数》（1572）中就已运用代数方法解决了。让我们看一个简单例子：把√2表示为连分数形式。其做法是：

整个求解过程合并起来可表示如下：

考察这个结果会发现一点令人惊讶的事情：√2这个无理数用小数表示时是一个无限不循环小数，但当用连分数表示它时，有序出现了：其部分商是循环的，而且循环节非常简单，只有一位。这种在开头的一些项后，由不断重复的有限项构成的连分数称为周期的，其循环周期称为循环节，节内的项数称为循环节长度。人们引入一种简便方法表示这类连分数，如√2的连分数形式可表示为。数字上面的横线表示循环节，以区别于普通循环小数的“点”式记号。

不仅√2的连分数具有这种特征，1770年，法国数学家拉格朗日证明了：任何一个二次无理数都有一个连分数展开式，这个展开式从某点往后是循环的。作为特例，他还证明了不尽根式√N的连分数一定具有如下形式：。

也就是说，其循环必从第二项开始，到2a1这项为止。除去最后一项2a1以外，循环部分是对称的，对称部分可以有中心项，也可以没有中心项。

为了应用方便，我们再提一种把不尽根式√N展为连分数的算法，为此要先额外引进Pn，Qn：

其中，，

利用以上的公式与规则，就可以更方便地把√N展开为连分数了。在把√N展为循环连分数之后，下一步我们可以考虑计算其渐近分数。对此，在前面我们已经介绍过一种可避免繁复计算的规则，即渐近分数可以用下面的递推公式迅速地算出来。

这样，借助以上给出的两个规则，就可求得√N的连分数形式及它的渐近分数了。比如，把√23化为连分数并求渐近分数可用表格形式把计算结果予以汇总如下：

不得不承认，这些规则本身是笨重而难记的。不过，在走过这一段艰辛的路程后，我们可以收获辛苦之后的果实了。事实上，√N的连分数展开式已为我们解决佩尔方程提供了所需要的一切工具。这只需要再借助于渐近分数的一项重要性质：。当Qn+1=1时，即有。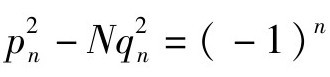

显然，若n是偶数则问题已完全解决，佩尔方程的一个特解是（pn，qn）。这里的n是使Qn+1=1的那个下标值。举个简单例子说明一下。

例：求佩尔方程x2-23y2=1的一个特解。

解：根据上面的表格，可以看到Q5=1。n=4为偶数，于是有，这样就可由渐近分数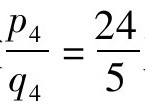直接得到x2-23y2=1的一个特解（24，5）。

由于事实上可以证明，n恰好是√N连分数展开式的循环节长度。因此，我们还可以稍微简化一下：先根据第一条规则求得，由于其循环节长度n=4是个偶数，所以可由渐近分数直接得到x2-23y2=1的一个特解。

如果n是奇数呢？此时（pn，qn）给出的是x2-Ny2=-1一个特解。在这种情况下，为了得到x2-Ny2=1的一个特解，一种办法是向后移动到第二个循环考虑2n项，此时一定有：。因此，一定是佩尔方程的一个特解。不过，应用婆罗摩笈多引理可以得到另一种更简单的方法。我们举例简单说明一下。

例：求佩尔方程x2-29y2=1的一个特解。

解：首先，根据上面第一条规则，可以求得√29的展开式是。由于其循环节长度n=5是个奇数，所以我们需要推移到下一个循环节，用第二条规则可得到其第十个渐近分数是，于是x=9801，y=1820便是x2-29y2=1的一个特解。比较简单的方法利用婆罗摩笈多引理。为此先得到第五个渐近分数。于是x=70，y=13是x2-29y2=-1的一个特解。由于婆罗摩笈多引理针对的是Nx2+k=y2形式的方程，因此我们需要做点小的转换。即把上面的结果化为：y=13，x=70是29y2-1=x2的解。这样即可得到y=2×13×70=1820，x=29×（13）2+（70）2=9801是29y2+1=x2的一个特解。即亦x=9801，y=1820是x2-29y2=1的一个特解。

再举一例：求佩尔方程x2-313y2=1的一个特解。

解：首先根据第一条规则可以得到，去掉循环部分的最后一个数字，即34，并利用第二条规则计算渐近分数，得到：

因为循环节长度是17，因此我们得到的是x2-313y2=-1的特解。再利用婆罗摩笈多引理，可进一步可求得x2-313y2=1的一个解为：

x=32188120829134849，y=1819380158564160。

一般地，设N为正整数且非完全平方数，将√N的连分数记为，并令其渐近分数p/q=[a,b1，

b2，……，br-1]，则（p,q）是方程x2-Ny2=（-1）r的解。若r为奇数，则我们直接得到佩尔方程x2-Ny2=1的解为（p,q）；如果r为偶数，则首先得到的是x2-Ny2=-1的解，随后可以借助婆罗摩笈多引理得到佩尔方程x2-Ny2=1的解为（p2+

q2N，2pq）。简单说，佩尔方程x2-Ny2=1的解为。

这一结论表明，佩尔方程x2-Ny2=1总是有解的，而且可以证明通过连分数法得到的这个解还一定是佩尔方程的最小正整数解。

佩尔方程有一个出人意料的奇异性质：其最小解随N的不同有很大不同。小于100的“高难度”N值（这些N值得出的x的最小值大于1000）包括：29、46、53、58、61、67、73、85、86、89、93、94、97。而其中难度最大的是婆罗摩笈多曾经研究过的61x2+1=y2。这或许正是与之相关的佩尔方程经常被提起的原因吧！

英国谜题专家Henry Ernest Dudeney在其1917年出版的一部著作《趣味数学》中，介绍了取材于哈斯廷斯之战（这一战争是1066年10月14日由哈罗德国王率领的撒克逊人和征服者威廉率领的诺曼底人之间爆发的一次著名冲突）的一个有趣问题。据一部关于此战役的史书记载：“哈罗德的士兵按照他们的惯例整齐地站在一起，排成了61个方队，每个方队中的士兵数目一样多……当哈罗德国王投入战斗时，参战的全部撒克逊人就构成了一个巨大的方队。”Dudeney提出的问题是，哈罗德国王的军队最少有多少名士兵？利用一点代数知识，就可列出下面的二次不定方程：61x2+1=y2。y2就是撒克逊人（包括哈罗德国王本人在内）的士兵总数。根据上面已介绍的结果，我们可得出士兵总数最小解为：3，119，882，982，860，264，401，即大约311万万万亿人。

在得到最小正整数解的基础上，还可以再进一步得到佩尔方程的所有正整数解。关于此，已有可利用的完整结论：

设（x0，y0）是x2-Ny2=1的最小正整数解，则它的每个正整数解可通过取幂得到：，（n=1，2，3……）

例如，佩尔方程x2-2y2=1的最小解为（3，2），那么其所有解可以对3+2√2取幂得到。比如，（3+2√2）2=17+12√2将给出方程的第二组解：x=17，y=12；（3+2√2）3=99+70√2将给出方程的第三组解：x=99，y=70等。

如果你兴致未尽，我们还可以继续前进，找到一个更方便的递推结果。x2-Ny2=1（N是非平方数），在最小正整数解之后，其正整数解依次的数值服从以下确定的法则：

xn=2axn-1-xn-2，yn=2ayn-1-yn-2，n≥2，x0=1，y0=0，a是第一组非零解中的x值。

利用这一有用的法则，可以更方便地在已知最小正整数解的前提下，依次求出佩尔方程的其他所有正整数解。

至此，我们已经对如何求解佩尔方程有了一个比较完整的介绍。在这一介绍中，我们再次与连分数打交道，并发现它提供了一种寻找佩尔方程最小正整数特解的最直接有效方法。在求解一次不定方程与佩尔方程时表现出来的优美与用处，体现了连分数的价值。作为数论领域中为数寥寥无几的直接方法之一，我们在此简单回顾一下连分数理论的发展。

连分数思想的最早期线索是不甚了然的。因为许多古代的数学结果只是对这种分数的一种启发，当时并不存在这一课题的系统发展。求两个数最大公约数的欧几里得算法在本质上就是把一个分数化为连分数的方法。这或许是连分数概念发展的最早的重要一步。而在解一次不定方程时，由于各种方法在本质上与连分数法相同，因此在此过程中如古印度数学家可能对连分数已有所了解。

连分数的近代理论始于意大利数学家邦贝利（1526～1572）。1572年，他出版的《代数》一书中包括一章平方根。在这一章中，他第一个用连分数来逼近平方根。为求√2等的近似值，他使用了其连分数。下一个考虑连分数的是意大利数学家卡塔尔迪（1552～1626），他在1613年发表了论述连分数的著作。第三个作者是德国数学家施文泰尔（1585～1636）。再之后，对连分数发展作出重要贡献的是英国皇家学会第一任会长的布朗克尔。其成果多发表于与其一直保持密切联系的沃利斯的著作中。如布朗克尔曾给出4/π的连分数表达式，这一结果发表在沃利斯的《无穷算术》（1655）一书中。除发表好友关于连分数的研究外，沃利斯本人对连分数也有发现。在《数学著作集Ⅰ》（1695）中他引入了“连分数”这一名称，叙述了一般连分数的渐近分数的许多初等性质，其中计算渐近分数的递推法则也是由他最早给出的。其后，欧拉、拉格朗日等数学家都倾注很大热情于连分数的研究。1737年，欧拉发表重要论文“连分数”为连分数的现代理论奠定了基础。

拉格朗日则在1767～1780年所发表的文章中，给出了用连分数求方程无理根的近似方法，并且用连分数的形式给出了微分方程的近似解。同时还证明了，二次方程的实根是周期连分数。

现在连分数在很多高深的数学分支中已成为不可缺少的数学工具，如在探索丢番图逼近这一领域，它现在是、将来可能仍然是入门阶梯。连分数本身也形成了自己独立的分支理论，它的研究还在继续深入展开。值得指出的是它在计算机上已有广泛应用，特别对于复杂函数的图形绘制和快速计算，它的作用更为突出。

佩尔方程有着悠久而迷人的历史，它首次出现在“阿基米得群牛问题”中。这一复杂的问题最终可以化成求解一个佩尔方程。但古希腊人只是提出了问题，对如何求解并没有留下任何记载。

求解佩尔方程的第一个有意义的进展出现于印度。628年，婆罗摩笈多阐述了求解佩尔方程的一种特殊方法，用他的方法有时可以得到一个初始解。同时婆罗摩笈多也给出了如何利用佩尔方程的一个初始解去得到新的无穷多组解的方法。自婆罗摩笈多之后，这一问题成为印度数学研究的中心问题之一，还特别给予专门的名称：瓦格布拉蒂。约500年后，古印度最伟大的数学家婆什迦罗对其解法作出重大改进。于是，经过婆罗摩笈多与婆什迦罗联手，古印度人在12世纪时得到了关于佩尔方程初始解的完整解答。非常遗憾的是，他们令人吃惊的颇具现代味道的开创性工作在很长时间里都不被欧洲人所了解。实际上，婆什迦罗的专著英译本于1817年才出版。由于传到欧洲太迟，结果印度人在这一问题上的工作没有在欧洲产生重要影响。

由于不知晓印度人的研究，关于佩尔方程及其研究在欧洲不得不等待着被重新发现。时光如梭，日历翻到了17世纪。法国数学家费马最早在欧洲重提佩尔方程问题。

1657年2月，在一封写给法国数学家弗雷尼克尔（约1605～1675）的信中费马提出求不定方程Nx2+1=y2的解的问题。费马信中指出：当N是正的非完全平方数时，这一方程有无穷多正整数解。在同一封信中，他向英国数学家挑战：求出这一方程的无穷多正整数解。后来费马又断言自己能确定更一般的方程x2-Ny2=m何时有整数解，并在可解时能把它解出来。不过，费马对自己的这些结论没有给出清楚的解释，他的方法也没有留传下来。但费马向欧洲数学家的挑战，刺激许多数学家对此作出研究。很快，重要进展就出现了。

1657年，英国皇家学会的第一任会长布朗克尔（1620～1684）勋爵首获成功，他得到了求解佩尔方程初始解的一般方法：连分数法。弗雷尼克尔则很快得到了Nx2+1=y2在N不超过150时各个方程的解。作为挑战的继续，弗雷尼克尔要求声称已有解决方法的布朗克尔求解313x2+1=y2。布朗克尔接受挑战，他用连分数法得到了这个佩尔方程的最小解，并说他搞定这个问题只用了一两个小时。在上面，我们已经简单求解了这一方程，但省略了具体过程。事实上，真正用连分数法解此方程，会体味到此项工作之艰巨，在一两个小时内求得这个解，并非容易的事。

与布朗克尔关系密切的另一位英国著名数学家沃利斯（1616～1703）对此也作出了贡献，他重新发现并证明了婆罗摩笈多引理。这意味着，只要能找到佩尔方程的一个初始解，就可以得到这一方程的无穷多个解。1658年，沃利斯公布了布朗克尔的方法与自己的研究。若干年后，沃利斯在其书《历史的和实用的代数学》（1685）中又对此做出重述。然而，荣誉却戏剧性地落在另一位其实对此并没有作出重要贡献的英国数学家佩尔身上。

佩尔（1611～1685）是英国数学教授，13岁时进入剑桥的三一学院，20岁以前就掌握了八门外语，1663年被选为皇家学会会员。佩尔也研究过这类方程。但正如我们已经介绍过的，他不是第一个研究它的人，也不是第一个解决它的人。他在这方面没有作出任何独立的贡献，事实上他所做的仅仅是在拉恩《方言代数》英译本的增补中，附录了布朗克尔的求解方法与沃利斯的研究结果。后来，伟大数学家欧拉读到了此书，惊叹解法的优美。然而他却一时失察，错误地认为书中的方法属于佩尔，于是欧拉把功劳归到佩尔身上，在1732年发表的一篇论文中把这类方程命名为佩尔方程。尽管佩尔和这个方程不再有其他任何瓜葛，然而因为伟大数学家欧拉的误会，佩尔却借着这个沿用至今的错误，赢得了数学上的不朽。虽然有人提出，为了澄清历史，“佩尔方程”的一个更好的名称应为“B3方程”，以此纪念三位姓氏以B开头的数学家——婆罗摩笈多（Brahmagupta）、婆什迦罗（Bhaskaracharya）、布朗克尔（Brouncker），然而更可能的结果是，佩尔驻足在大人物失误基础上获得的荣誉会一直保留下去。没错，这个方程现在仍被称为“佩尔方程”。

在欧拉之后，拉格朗日开始对这个问题进行了全面研究。

1767年，拉格朗日第一次运用连分数理论，即应用√N的连分数展开式证明了佩尔方程x2-Ny2=1总有解。

1770年，拉格朗日在重要论文“整数不定问题解的新方法”中又解决了更一般的x2-Ny2=B的解的存在性及求解问题。他同时还讨论了更广泛的二元二次整系数方程ax2+2bxy+cy2+2dx+2ey+f=0并解决了其整数解问题。为此，他还开辟了二元二次型的一般理论。

以下引述的两封写给朋友的信可以让我们体会到拉格朗日为此的付出。

“最近几天我一直在用一些算术问题来使我的研究有点变化。我向你保证，我发现的困难比我预期的多得多。例如，这就是我费了很大力气才得出解答的一个问题。已知任一不是平方数的正整数n，求一个整数的平方x2，使nx2+1是一个平方数。这个问题在方幂理论（现在的二次型）中具有很大的重要性，而（方幂）在丢番图分析中是主要的研究对象。”（1768年8月15日）

“我谈到过的问题让我花了比我预想的要多得多的时间；但是最后我很高兴地结束了。我相信我实际上已经完全解决了两个未知数的二次不定方程的问题。”（1769年2月28日）

就这样，佩尔方程及更一般的二元二次整系数方程的理论研究以1770年拉格朗日的论文发表而告终结了。