配流副楔形油膜压力分布的计算

配流副的油膜厚度通常在8～22μm，根据油膜润滑理论，做如下假设，以简化计算：

（1）沿润滑膜厚度h（一般h很小）方向上，忽略压力的变化，即∂p/∂y=0。

（2）运动副表面的曲率半径与油膜厚度h相比要大得多，故可以不计表面运动速度方向的改变。

（3）油液运动时的惯性力与黏性力相比可以忽略不计。

（4）油液在间隙中的流动为层流。

（5）油液是不可压缩的流体。

建立坐标如图9.5所示，表面1与表面2之间为流体润滑膜。表面1和表面2处于运动中。流体膜中任取点P，对应三个坐标方向x、y、z的流速分别为u、v、w。过P点做垂直于x Oy平面的直线，分别交表面l、表面2于P1、P2点，则如图所示P点油膜的厚度为h=h2－h1。

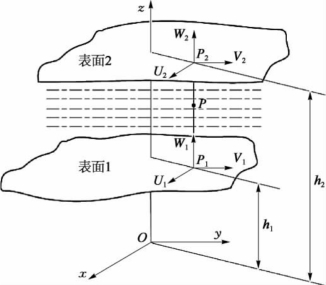
图9.5　坐标系和固体表面

对于流体膜，z方向的尺寸比x方向及y方向的尺度小若干个数量级，则与速度梯度∂u/∂z、∂v/∂z相比较，其他速度梯度均为高阶小量，可以忽略。根据假设，不计流体的体积力、惯性力，可以得出对应x方向的应力及其变化关系。x方向的受力分析可得

由牛顿黏性定律，代入上式得

同理，在y方向可得

将方程式（9.15）和式（9.16）对z积分两次得

根据无滑动速度边界条件：z=h1时，u=U1；z=h2时，u=U2，得积分常数C1、C2为

代回式（9.17），得

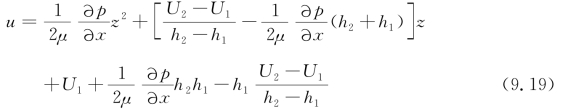
同理，可以得出y方向的流速为

定义x方向的体积流量为

将式（9.19）代入，完成积分，且h=h2－h1，得

同理

记质量流量为mx=ρqx，my=ρqy，则有

由流体力学知，一般流体的连续性方程为

对变量z积分并应用无滑动速度边界条件：z=h1时，w=W1；z=h2时，w=W2，得

其中

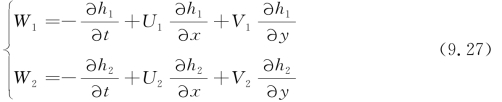
又由于

将该法则用于式（9.27），得

将式（9.7）、式（9.8）分别代入式（9.27），化简积分后的连续方程为

将式（9.24）代入式（9.30），整理得

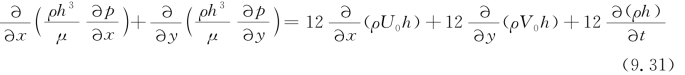
其中

故由N-S方程及流量连续方程可建立配流副油膜压力场控制方程，为

式中，p为密封带内的压力；h为油膜厚度；μ为液压油黏度；U为配流盘表面油膜速度。

柱坐标下的控制方程式为

其中可由式（9.11）求得

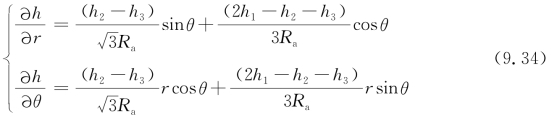
将油膜划分为网格，采用差分法解压力分布，如图9.6所示。用逐个节点上的压力值构成各阶差商，近似取代雷诺方程中的导数，将方程化为一组代数方程，由此解出各节点上的压力值。所得离散压力数值，近似表达了油膜中的压力分布。

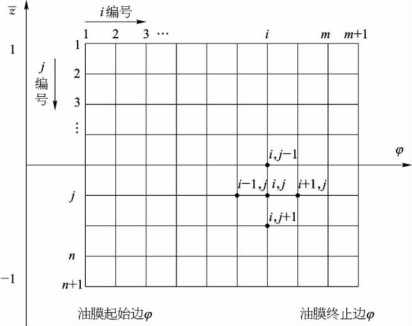
图9.6　差分网格法

对无量纲化雷诺润滑方程式（9.33）进行离散化，将网络节点按所在的列数和行数顺序编号，沿φ方向的列数用i编号，沿z方向的行数用j编号，每个节点的位置用（i，j）二维编号表示，如图9.6所示。设在φ方向共均匀划分为m格，i的编号即从l到m+1，每格宽度（步长）为Δφ=（φ2－φ1）/m；在z方向均分为n格，则j编号从1到n+l，步长为Δz=2/n。为便于编程计算，取压力分布函数p（φ，z）的两个自由变量的节点数为40×40。任意点p（i，j）的一阶和二阶偏导数都可由周围节点变量值表示。

对p（xi+1，yj）进行泰勒展开

对p（xi－1，yj）进行泰勒展开

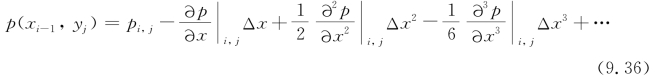
采用中差分公式，则变量p在p（i，j）点的偏导数为

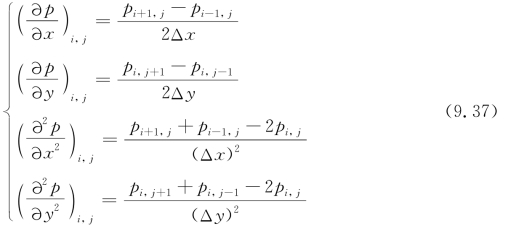
将雷诺方程写成二维二阶偏微分方程的标准形式

将式（9.37）代入式（9.38），各节点变量pi，j与相邻节点变量的关系式可写为

式（9.38）适用于全部内节点（i=2～m，j=2～n），因此共有（m－1）×（n－1）个式（9.39）构成一组对于（m－1）×（n－1）个内节点pi，j值的线性非齐次代数方程，从而可解出各个内节点的pi，j值。其中各系数为

对方程式（9.38）求解得

该方程组的求解，多种数值迭代计算方法均适用，如牛顿迭代法、超松弛迭代法等，在此不做求解过程介绍。