单层前馈神经元网络（感知器）

20.5.3 单层前馈神经元网络（感知器）

如果网络的所有输入直接连接到输出，就称为单层神经元网络，或称感知器网络。因为每个输出单元与其它输出单元无关——每个权值只影响一个输出——所以我们可以简化一下，只考察一个输出单元，如图20.19（a）中所示。

图20.19 （a）一个感知器网络，由3个感知器输出单元组成，它们共享5个输入。观察一个特定的输出单元（比如说第二个单元，轮廓为黑色的），我们可以看到它的输入边的权值对其它输出单元没有影响。（b）两输入的S型激励函数感知器单元的一个输出结果图

让我们从查看一个感知器可以表示的假设空间开始。利用阈值激励函数，我们可以将感知器视为对一个布尔函数的表示。除了基本的布尔函数AND、OR以及NOT（见图20.17）外，感知器可以很简洁地表示一些相当“复杂”的布尔函数。例如，多数函数，只有当n个输入中超过半数为1时，输出才为1，它可以用一个感知器表示，其中每个Wj= 1，阈值W0= n / 2。决策树则需要O(2n)个节点才能表示这个函数。

不幸的是，有许多布尔函数用阈值感知器无法表示。观察公式（20.10），我们看到当且仅当输入（包括偏差单元）的加权和是正值时，阈值感知器才会返回1：

这里，式W · x ＝ 0定义了一个输入空间中的超平面，所以当且仅当输入位于超平面的某一侧时感知器才返回1。由于这个原因，阈值感知器也被称为线性分类器。图20.20（a）和（b）显示了对应的超平面（在二维平面上是一条直线），感知器表示的分别是两输入的AND和OR函数。黑点指示输入空间中的一点，在那里函数值等于1，而白点指示的是值为0的点。感知器之所以可以表示这些函数，是因为存在某条直线可以将所有的白点与所有的黑点分隔开。这样的函数也被称为线性可分的。图20.20（c）显示了一个非线性可分的函数的例子——XOR（异或）函数。很显然，任何阈值感知器都无法学习这个函数。通常情况下，阈值感知器只能表示线性可分的函数。这只是所有函数中的一小部分，习题 20.14 要求你确定这个部分的数量。S 型感知器也有类似的局限，它们只能作为“软”线性分类器（参见图20.19（b））。

图20.20 阈值感知器的线性分类能力。黑点指示了输入空间中函数取值为1的点，白点指示了取值为0的点。对于直线的无阴影一侧的区域，感知器的返回值都是1。在（c）中，不存在这样的能正确对输入进行分类的直线

尽管表达能力有限，阈值感知器还是有一些优点的。尤其是，存在一个简单的学习算法，使得一个阈值感知器能适合任何线性可分的训练集。与其描述这个算法，我们不如推导出一个与此非常相关的算法，用于S型感知器的学习。

这个算法背后的思想是调整网络的权值，使得训练集上的某种误差度量达到最小，这实际上也是大部分神经元网络算法背后的思想。如此，学习过程可以形式化为权值空间 [19]中的一个最优化搜索问题。“经典的”误差度量是误差平方和，我们在第 20.2.3 节的线性回归中曾经使用过。对于输入为 x的单个训练样本，与真实输出y之间的平方误差可以写成：

其中hw(x)是感知器对该样本的输出结果，而y是真实输出值。

通过计算E对每个权值的偏微分，我们可以使用梯度下降法减小平方误差。我们得到

其中g' 是激励函数的导数 [20]。在梯度下降算法中，我们想要降低E，于是进行权值的更新如下：

其中α 是学习速率。直觉上看，这应该很有意义。如果误差Err = y − hw(x)是正的，则网络的输出过小，所以对于正的输入要增加权值，而对于负的输入要减小权值。如果误差是负的，正好相反。[21]

完整的算法如图 20.21 所示。每次有一个训练样本通过网络，然后在每个样本之后调整权值以减小误差。处理全部样本的每次循环称为一代。一代一代地重复进行直到达到了某个停止标准——典型情况下，停止标准是权值的改变已经很小了。其它方法则对整个训练集计算梯度，计算是通过在更新权值之前累加公式（20.12）中得到的所有梯度贡献而完成的。随机梯度方法从训练集中随机选取样本，而不是用循环的方式。

图20.21 感知器的梯度下降学习算法，其中定义了一个可微分的激励函数g。对于阈值感知器，因子g'(in)在权值更新时被忽略了。NEURAL-NET-HYPOTHESIS返回一个用于对任何已知样本计算网络输出的假设

对于所有权值，g'(in)都相同，所以忽略它仅仅会改变对每个样本的总体权值更新的量级，而不会改变更新的方向。

图20.22显示了一个感知器在两个不同问题上的学习曲线。在左边，我们显示了有11个布尔输入的多数函数的学习曲线（即，如果有6个或者更多的输入为1则函数的输出为1）。如我们所预期的，由于多数函数是线性可分的，感知器很快就学会了这个函数。另一方面，决策树学习器则没有什么进展，因为多数函数很难（虽然不是不可能）表示为一棵决策树。在右边，我们看到的是餐馆实例。求解的问题很容易表示为一棵决策树，但它不是线性可分的。穿过数据的最佳平面的分类正确率只有65％。

图20.22 感知器与决策树的比较。（a）对于学习11个输入的多数函数，感知器更合适。（b）对于学习餐馆例子中的WillWait谓词，决策树更合适

到目前为止，我们把感知器当作可能有错误输出的确定性函数对待。也可能把S型感知器的输出解释成一个概率——特别是，给定输入情况下真实输出为1的概率。根据这种解释，可以将S型感知器用作贝叶斯网络中条件分布的一个规范表示（参见第 14.3 节）。还可以用最大化数据的（条件）对数似然的标准方法得到一条学习规则，如本章前面部分所述。下面来看看具体的过程。

考虑单个训练样本，真实输出值为T，并且令p是这个样本由感知器返回的概率值。如果T = 1，则数据的条件概率是p；如果T = 0，则数据的条件概率是(1 − p)。现在我们可以用简单的技巧写出一个可微分形式的对数似然。这个技巧就是将表达式的指数中的0/1变量当作一个指示变量：当T = 1，pT为p，否则为1；同样，如果T = 0，则(1 − p)(1−T )为(1 − p)，否则为1。因此，我们可以写出数据的对数似然如下：

由于S型函数的特性，梯度下降简化为一个非常简单的公式（参见习题20.16）：

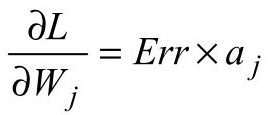
注意，S 型感知器中最大似然学习的权值更新向量与用于最小化平方误差的更新向量在本质上是相同的。因此，我们可以说感知器有一个概率解释，即使当学习规则来自一个确定性的观点时。