你知道布拉德雷(Bradley)发现的光行差现象是什么。从恒星发出的光通过望远镜要花费一定的时间;在这段时间内,由地球运动携带着的望远镜也移动了。因此,如果把望远镜对准恒星的真实方向,当光线到达物镜时,那么在网络的十字线占据之点就形成了物象;当光线到达网络的平面时,这个十字线便不在同一点了。从而要使物象落在十字线,我们不得不稍为改变一下望远镜的方向。结果,天文学家将不把望远镜对准光线绝对速度的方向,也就是说朝向恒星的真实位置,而恰恰对准光线参照于地球的相对速度方向,也就是说朝向所谓的恒星表观位置。
光速是已知的;因此我们可以假定,我们具有计算地球绝对速度的手段。(我马上将要说明我在这里使用的绝对一词。)没有这种事;我们确实知道我们所观察的恒星的表观位置;但是,我们并不知道它的真实位置;我们只知道光速的大小,而不知道光速的方向。
因此,假如地球的绝对速度是匀速直线的,我们从来也不会猜想光行差现象;但是,它是可变的;它由两部分组成:太阳系的速度,这是匀速直线的;地球相对于太阳的速度,这是可变的。如果只存在太阳系的速度即恒定的部分,那么观察到的方向就是不变的。人们如此观察到的这个位置被称为恒星的平均表观位置。
现在,同时考虑地球速度的两部分,我们将有实际的表观位置,它绕平均表观位置描绘出一个小椭圆,我们观察到的正是这个椭圆。
忽略很小的量,我们将看到,这个椭圆的大小仅取决于地球相对于太阳的速度与光速之比,因此只有地球对于太阳的相对速度起作用。
不过,请等一等!这个结果不是精密的,而仅仅是近似的;让我们把近似度稍微向前推进一下。于是,这个椭圆的大小将取决于地球的绝对速度。让我们针对不同的恒星比较椭圆的长轴:我们至少在理论上将有办法决定这个绝对速度。
这事也许没有乍看起来那样令人震惊;事实上,问题不在于相对于绝对虚空的速度,而是相对于以太的速度,按定义,以太被认为是绝对静止的。
而且,这种方法纯粹是理论性的。实际上,光行差是很小的;光行差椭圆的可能变化还要小得多,如果我们考虑光行差是属于一阶量的,从而这些变化可视为二阶量:大约百万分之一弧秒;我们的仪器绝对察觉不到它们。最后,我们将进一步看到,为什么应该抛弃前面的理论,为什么我们不能决定这个绝对速度,即使我们的仪器精确一万倍!
人们可以设想一些其他方法,事实上人们已经这样做了。光速在水中与在空气中并不相同;先通过充空气的望远镜,然后通过充水的望远镜,观察恒星的两个表观位置,难道我们不能把二者加以比较吗?结果是否定的;地球运动并没有改变反射和折射的视定律。这个现象可以有两种说明:
1°可以假定以太不是静止的,不过它却被运动的物体曳引着。于是,地球运动没有改变折射现象,这一点也不奇怪,因为三棱镜、望远镜和以太这一切东西被曳引一起作同一平移。至于光行差本身,可以用在星际空间中的静止以太和被地球运动所曳引的以太之分界面上所发生的折射种类来说明。正是基于这个假设(以太完全被曳引),建立了关于动体电动力学的赫兹(Hertz)理论。
2°相反地,菲涅耳(Fresnel)假定,以太在虚空中是绝对静止的,在空气中几乎是绝对静止的,不管空气的速度多大,而且以太只能部分地被折射媒质曳引。洛伦兹给这种理论以更满意的形式。在他看来,以太是静止的,只有电子处于运动之中;在虚空中,仅仅是以太的问题,在空气中,情况几乎是这样,曳引是零或几乎是零;在折射媒质中,扰动是同时由以太的振动和通过以太扰动而处于飘游中的电子的振动引起的,波动部分地被曳引。
为了在这两个假设之间裁决,我们有斐索(Fizeau)实验,该实验通过测量干涉条纹比较静止空气或运动空气中的光速。这些实验确认了菲涅耳的部分曳引假设。迈克耳孙(Michelson)以同样的结果重复了这些实验。因此,必须拒斥赫兹理论。
但是,如果以太不被地球的运动曳引,借助光现象可以证明地球的绝对速度,或更确切地讲,可以证明地球相对于不动以太的速度吗?实验做出了否定的回答,可是人们还是以所有可能的方式改变实验程序。无论使用什么方法,永远只能揭示出相对速度;我意指某些物体相对于其他物体的速度。事实上,如果光源和观察仪器在地球上并参与地球的运动,那么实验结果总是相同的,不管仪器相对于地球轨道运动的取向是什么。如果光行差出现了,那正是因为光源即恒星相对于观察者在运动着。
如果我们忽略光行差的二阶微量,迄今的假设完全可以阐释这一普遍结果。该说明依赖于洛伦兹引入的地方时概念,我将力图弄清楚它。设有两个观察者,一个位于A,另一个位于B,希望借助于光信号来对他们的钟。他们商定,当他的钟指向一个确定的时刻时,B将发出一个信号给A,而A在看到信号时把他的钟拨到那个时刻。如果仅仅是这样做,会存在系统误差,因为当光从B到A时要花费某一时间t,A的钟比B的钟慢时间t。这个误差容易矫正。交叉信号就足够了。A反过来也必须向B发信号,在这一新校准之后,B的钟将比A的钟慢时间t。于是,取两次校准的算术平均值将是充分的。
但是,这种做法假定,光从A到B与光从B返回A要花费相同的时间。如果观察者是不动的,这是正确的;如果他们被曳引公共平移,情况就不再是如此了,例如,这是因为A到那时将遇到从B发出的光,而在光来自A之前,B将离开。因此,如果观察者一起具有公共平移,如果他们不怀疑这一点,那么他们的校准将是有缺陷的;他们的钟将不是指示同一时间;每一个钟都将显示属于它所在地点的地方时。
如果不运动的以太只能向他们传达都是同一速度的光信号,如果他们可以发出的其他信号都是通过与他们一起被曳引平移的媒质传播的,那么两个观察者将无法觉察到这一点。每一个人观察到的现象将太早或太迟;只有当不存在平移,才会在同一时刻看到它;可是,由于用表观察到的东西是错的,而又觉察不到这一事实,从而外观将没有什么变化。
由此可知,只要我们忽略光行差的平方,补偿就很容易得到说明,长期以来,实验并没有精确得足以有理由考虑它。但是,直到有一天,迈克耳孙构想出更为精妙的程序:他使沿不同路线传播的光线在平面镜反射后发生干涉;每一条路径大约是一米,干涉条纹许可辨认千分之一毫米,从而就不再能忽略光行差的平方了,可是结果还是否定的。因此,需要完善理论,它由洛伦兹-斐兹杰惹假设完成了。
这两位物理学家假定,所有被曳引平移的物体都在平移的方向经受收缩,而它们的垂直于平移方向的尺度依然不变。这种收缩对于所有物体来说都是相同的;而且,它很小,对于像地球那样的速度而言,它大约是二亿分之一。此外,即使我们的测量仪器精密得多,也无法揭示它;事实上,我们的量杆像被测量的物体一样,经历相同的收缩。如果我们把物体以及米尺对准地球运动的方向,米尺与所测量的物体严格相符,那么在另一取向它们依然严格相符,尽管物体和米尺在长度以及取向上都发生了变化,这恰恰是因为变化对于物体和对于米尺来说是相同的。可是,如果我们现在不是用米尺,而是用光通过物体所花费的时间来测量长度,那情况就完全不同了,这正是迈克耳孙所做的事情。
在静止时的球体,当它运动时就变成扁平的旋转椭球体的形状;可是观察者将总是认为它是球体,因为他本人也经受了类似的形变,所有作为参照点的物体也是如此。相反地,严格保持球形的光的波面在他看来似乎被拉长为椭球面。
接着发生了什么呢?设观察者和光源一起被携带平移:从光源发出的波面将是球面,这些球面以光源的相继位置为中心;从这个中心到光源的实际位置的距离将与在发射后逝去的时间成正比,也就是说与球面的半径成正比。因此,所有这些球面关于光源的实际位置S互为同位相似球面。可是,对于我们的观察者来说,由于收缩,所有这些球面将似乎拉长成椭面,而且所有这些椭面关于点S将是同位相似椭面;所有这些椭面的离心率是相同的,只取决于地球的速度。我们将如此选择收缩定律,以便使点S可以处在椭球的子午面的焦点上。
这时,补偿是严格的,人们正是这样说明迈克耳孙实验的。
我上面已经说过,按照通常的理论,光行差的观察会给出我们地球的绝对速度,如果我们的仪器精密一千倍的话。我必须修正这种说法。是的,观察到的角度会被这一绝对速度的效应修改,但是我们用来测量角度的分度圆却会因收缩而发生形变:它们变成了椭圆;从而导致所测量的角度出现误差,这第二种误差可以精确补偿第一种误差。
乍看起来,这种洛伦兹-斐兹杰惹收缩似乎是异乎寻常的;此刻,我们能够说的有利于它的一切就是,如果我们用光通过一长度所需要的时间来定义长度,那么这只不过是迈克耳孙实验结果的直接翻译。
无论如何,情况也许是,不可能逃脱下述印象:相对性原理是普遍的自然定律,人们用任何想像的方法永远只能证明相对速度,所谓相对速度,我不仅意指物体相对于以太的速度,而且也意指物体彼此相关的速度。如此之多的不同实验给出了一致的结果,以致我们感到被诱导把相称的价值赋予相对性原理,例如与当量原理相称的价值。无论如何,恰当的做法是,看看这种观察事物的方法可以导致我们得到什么结果,然后把这些结果提交实验对照。
让我们看看,在洛伦兹理论中,作用和反作用相等原理变成什么。考虑一个电子A,它由于某种原因开始运动;它在以太中产生扰动;在某一时间末,这种扰动到达另一个电子B,B将离开它的平衡位置。在这些条件下,作用和反作用之间不能相等,至少在我们不考虑以太,而只考虑电子的情况下是这样,电子是唯一可观察的,由于我们的物质是由电子构成的。
实际上,正是电子A扰动了电子B;即使在电子B可以作用于A的情况下,这种反作用可以等于作用,但是也绝不是同时的,因为电子B只有在传播所必需的某一时间之后才能开始运动。把这个问题提交比较精确的计算,我们达到下述结果:设把一个赫兹放电器置于抛物柱面镜的焦点,与之机械相接;这个放电器发射电磁波,镜子向同一方向反射所有这些波;因此,放电器将向确定的方向辐射能量。好了,计算表明,放电器像发射出炮弹的大炮一样反冲。在大炮的例子中,反冲是作用和反作用相等的自然结果。大炮之所以反冲,是因为受到大炮作用的炮弹对大炮发生反作用。但是在电子的例子中,情况不再相同了。发出的东西不再是实物炮弹:它是能量,而能量没有质量:它没有对应物。我们可以仅仅简单地考虑一个带有反射器的灯,来代替放电器,反射器可以把灯的光线集合到一个方向。
的确,如果从放电器或从灯发射的能量遇到实物对象,这个对象便受到机械推力,犹如它受到真实炮弹撞击一样,而且这一推力将等于放电器和灯的反冲力,倘若在途中没有能量损失且对象吸收全部能量的话。因此,人们被诱使说,在作用与反作用之间还存在着补偿。但是,这种补偿即便是完备的,可也总是延迟的。如果光在离开光源后,通过星际空间漫游一直没有遇到实物物体,那就永远也不会发生补偿;如果受冲击的物体不是完全吸收的,补偿就是不完备的。
这种力学作用太小以致无法进行测量吗,或者它们可受实验检验吗?这些作用无非是由麦克斯韦(Maxwell)-巴托利(Bartholi)压力引起的;麦克斯韦由静电学和磁学的计算预言了这些压力;巴托利根据热力学的考虑达到了同一结果。
彗尾正是这样被说明的。小粒子本身是从彗核中分离出来的;它们受到太阳光的冲击,太阳光把它们推向后部,犹如来自太阳的弹雨一样。这些粒子的质量如此之小,以致这种排斥力反抗牛顿引力而扫过彗星;这样,在离开太阳运动时,它们便形成彗尾。
直接的实验证实是不容易得到的。首次努力导致了辐射计的建造。这个仪器逆转,其方向与理论方向相反,自从它被发明以来,对它的旋转的说明是完全不同的。最后,一方面使真空更完善,另一方面不给叶片一面涂黑,直接使光线束照射在叶片一面上,终于取得了成功。辐射度的影响和其他扰动原因通过一系列的费力的预防办法被消除了,人们得到十分微小的偏离,不过这看来好像是与理论符合的。
我们在前面讲过的赫兹理论以及洛伦兹理论都同样预示了麦克斯韦-巴托利压力的同一效应。不过,还有差别。例如,设能量以光的形式通过透明媒质从光源到达任何物体。麦克斯韦-巴托利压力将不仅在离开时对光源、在到达时对被照射的物体施加作用,而且也对它传播时通过的透明媒质的物质施加作用。当光波到达这种媒质的新区域时,这种压力将把分布在那里的物质向前推,而在波离开这个区域时,它将把物质向后推。这样一来,光源的反冲力由于对应物而导致与光源接触的透明物质向前运动;稍后,这同一物质的反冲力由于对应物而导致位于稍远处的透明物质向前运动,如此等等。
可是,补偿是完备的吗?不管透明媒质的物质是什么,麦克斯韦-巴托利压力对这种物质的作用等于它对光源的反作用吗?或者,像媒质较少折射能力且比较稀少一样,这种作用也小得多,以致在虚空中变为零吗?
赫兹把物质视为与以太机械地关联的,以致以太可以完全被物质曳引,如果我们承认赫兹的理论,那就必须对第一个问题回答是,对第二个问题回答否。
因此,即使在最小折射的媒质中,即使在空气中,即使在星际虚空中,也存在着像作用和反作用相等原理所要求的完备补偿,在那里足以假定有物质的残余,不管其多么稀薄。相反地,如果我们承认洛伦兹理论,那么补偿总是不完全的,在空气中是难以察觉的,而在虚空中变为零。
但是,我们在上面已经看到,斐索实验不容许我们保留赫兹理论;因此,必须采纳洛伦兹理论,从而必须抛弃反作用原理。
我们在上面看到迫使我们把相对性原理看做是普遍的自然定律的理由。让我们考察一下,这个原理会导致什么结果,是否能够认为它最终被证明。
首先,它迫使我们推广洛伦兹和斐兹杰惹关于所有物体在平移方向收缩的假设。尤其是,我们必须把这个假设延伸到电子本身。亚伯拉罕把这些电子看做是球形的和不会变形的;在我们看来,必须承认这些在静止时是球形的电子在运动时经受了洛伦兹收缩,从而形成扁平的椭球。
电子的这一形变将影响它们的力学性质。事实上,我已经说过,这些带电的电子的位移是确实的运流,它们的表观惯性源于这种电源的自感应:专就负电子而论;对于正电子而言,我们还不知道是否全部如此。好了,电子的形变取决于它们的速度,这一形变将改变它们表面的电分布,从而改变它们产生的运流的强度,改变这种电流的自感应作为速度的函数而变化的规律。
以这种代价,补偿将是完全的,而且符合相对性原理的要求,但只是在下述两个条件下才行:
1°正电子没有真实质量,而只有虚设的电磁质量;或者至少,即使它们的真实质量存在着,也不是常数,而是按照与它们的虚设质量相同的定律随速度变化。
2°所有的力都是电磁起源,或者至少,它们按照与电磁起源的力相同的定律随速度而变化。
还是洛伦兹,完成了这一引人注目的综合;让我们停一下,看看由此得出了什么结果。首先,不再存在物质,因为正电子不再具有真实质量,或者至少不再有不变的真实质量。我们力学的现存原理曾建立在质量不变的基础上,因而必须加以修正。再者,电磁说明必须考虑到所有已知的力,尤其是引力,或者至少引力定律必须如此修正,以便这种力按照与电磁力相同的方式随速度变化。我们还将回到这一点。
乍看起来,这一切好像有点人为色彩。尤其是,电子的这种形变似乎完全是假设性的。不过,事情可以用另外的方式来描述,以便避免在推理的基础上提出这一形变假设。把电子看做质点,询问在不违背相对性原理的情况下,它们的质量作为速度的函数应该如何变化。或者讲得更恰当一些,就是要询问:在电场或磁场的影响下,它们的加速度应该是什么,才不致违背相对性原理,而且当我们假定速度很小时,我们又回到通常的定律。我们将发现,质量的变化或加速度的变化必定像电子经受了洛伦兹形变似的。
于是,在我们面前有两种理论:一种是电子不可能形变的理论,这就是亚伯拉罕的理论;另一种是电子经受洛伦兹形变的理论。在两种情况下,它们的质量随速度而增加,当速度变得等于光速时,质量变为无穷大;不过,变化规律是不同的。考夫曼所使用的方法揭示出质量变化的规律,从而似乎给予我们在两种理论之间作出裁决的实验手段。
不幸的是,他的第一批实验不能足够精确地做到这一点;于是,他决定以较多的预防措施重复这些实验,十分细心地测量了场的强度。在其新形式下,这些实验有利于亚伯拉罕理论。于是,相对性原理不可能具有我们被诱使赋予它的严格价值;不再有理由相信正电子像负电子一样被剥夺了真实质量。然而,在肯定地采纳这个结论之前,有必要再做一点思考。问题是如此重要,以致人们希望另外的实验家(1)重复考夫曼实验。很不幸,这个实验十分棘手,只有具有与考夫曼同样才能的物理学家才能成功地进行。人们恰当地采取了一切预防措施,我们没有发现能够提出什么异议。
不过,还有一点我希望引起注意:这就是静电场的测量,一切均与这一测量有关。这个场是在电容器的两个极板之间产生的;在这两个极板间,必须造成极其完全的真空,以便得到完备的绝缘。然后,测量两个极板的电势差,用离极板的距离除以这个电势差便得到场强。这假定电场是均匀的,这是确定的吗?在一个极板的附近,例如负极板的附近,电势不会突然下降吗?在金属和真空的汇合处可能有电势差,这种电势差在正的一侧和负的一侧可以不同;导致我这样想的是水银和真空之间的电真空管效应。不管情况如此的几率多么小,似乎还应当考虑它。
在新动力学中,惯性原理还是正确的,也就是说,孤立的电子将作匀速直线运动。至少,这是普遍假定的;不过,林德曼(Lindemann)反对这种观点;我不想参加这一讨论,我在这里不能详述它,因为它具有过于困难的性质。无论如何,对该理论稍作修正,便会足以庇护它免受林德曼的反驳。
我们知道,浸在流体里的物体在运动时要经受显著的阻力,这是因为我们的流体是黏滞的;在理想流体中,完全没有黏滞性,物体会在其后激起液体小丘,某种类似于船的尾波的东西;开始时,必须用很大的力量才能使之运动,由于这不仅必须使物体本身运动,而且还必须使物体尾波的液体运动。但是,一旦获得运动,它就会毫无阻力地扰动自身,因为物体在行进中仅仅随之携带液体的扰动,液体的总活劲(vis viva)不会增加。因此,一切就好像惯性增加一样地发生着。在以太中前进的电子也以相同的方式行动:在电子周围,以太也会被激起,但是这种扰动伴随着物体而运动;因此,对于和电子一起被携带的观察者来说,伴随这个电子的电场和磁场似乎是不变的,只有在电子的速度变化时它们才可能变化。从而,要使电子运动就必须用力,由于必须产生这些场的能量;相反地,一旦获得了运动,就不需要力维持它了,由于所产生的能量仅仅像尾波一样在电子之后前进。因此,这一能量只是增加电子的惯性,正如液体的扰动增加浸在理想流体中的物体的惯性一样。无论如何,负电子至少没有除此以外的惯性。
在洛伦兹假设中,活劲仅仅是以太的能量,它不与υ2成比例。无疑地,如果υ很小,活劲明显地与υ2成正比,运动量明显地与υ成正比,两种质量明显不变且彼此相等。但是,当速度趋近于光速时,活劲、运动量和两种质量便超越所有限度而增加。
在亚伯拉罕的假设中,表达稍为复杂些;不过,我们刚才说过的东西本质上依然正确。
这样一来,当速度等于光速时,质量、运动量、活劲变为无穷大。
由此可得,没有什么物体能够以任何方式获得超越于光速的速度。事实上,随着物体速度的增加,它的质量也成比例地增加,于是它的惯性以越来越大的阻力对抗速度的任何新增加。
于是,问题提出来了:让我们姑且承认相对性原理吧;运动的观察者没有任何手段察觉他自己的运动。因此,如果没有一个处于绝对运动的物体能够超过光速,而可以像你乐意的那样接近光速,那么就它对于我们观察者的相对运动而言,情况应该相同。于是,我们可能被诱使如下推理:观察者可以获得200000公里的速度;对于观察者作相对运动的物体也可以得到同一速度;物体的绝对速度从而将是400000公里,这是不可能的,因为这已超过了光速。这仅仅是外表的假象,当考虑到洛伦兹如何估价地方时时,这种假象就消失了。
当电子运动时,它在它周围的以太中产生扰动;如果它的运动是匀速直线运动,这种扰动便化归我们上节所说的尾波。但是,如果运动是曲线的或变化的,情况就不一样了。于是,该扰动可以看做是两种另外的扰动的叠加,朗之万(Langevin)把这两种扰动命名为速度波和加速度波。速度波仅仅是在匀速运动中出现的波。
至于加速度波,这是完全类似于光波的扰动,它是电子在经受加速的时刻从电子发出的,从而它通过连续的球面波以光速传播。由此可得:在匀速直线运动中,能量完全守恒;但是,当有加速度时,就要损失能量,能量以光波的形式耗散,越过以太而传播到无穷远处。
不过,这种加速度波的效应,尤其是相应的能量损失,在大多数情况下是微不足道的,这就是说,不仅在普通力学中和天体运动中是这样,而且甚至在镭射线中也是如此,镭射线的速度很大,但却没有加速度。于是我们可以有限度地应用力学定律,使力等于加速度与质量之积,不过这个质量按照上面所说明的规律随速度而变化。因此我们说,该运动是准稳运动。
在加速度大的所有情况中,问题就不会一样了,这主要有下述几个方面:
1°在白炽气体中,某些电子作频率很高的振动;位移是很小的,速度是有限的,而加速度很大;从而把能量传给以太,这就是为什么这些气体辐射出与电子振动的周期相同的光。
2°相反地,当气体接收光时,这些相同的电子便以极强的加速度振动,它们吸收光。
3°在赫兹放电器内,在金属质量内环流的电子在放电的瞬间经受了突然加速,从而获得高频振动。由此便导致部分能量以赫兹波的形式辐射出去。
4°在白炽金属中,围在这种金属内的电子被激发而具有很大的速度;在接近金属表面时,由于它们不能通过表面,它们被反射从而经历显著的加速。这就是金属发射光的原因。用这种假设,可以圆满地说明黑体辐射光的定律的细节。
5°最后,当阴极射线撞击到对阴极时,构成阴极射线的、受到激励而具有极大速度的负电子突然受到阻碍。因为它们这样经受了加速,它们便在以太中产生波动。按照某些物理学家的观点,这就是伦琴(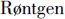 )射线的来源,伦琴射线也许只不过是波长很短的光线而已。
)射线的来源,伦琴射线也许只不过是波长很短的光线而已。
————————————————————
(1) 本书付印时,我获悉布赫尔(Bucherer)先生采取了新的预防措施,重复了这个实验,他得到了与考夫曼相反的结果,证实了洛伦兹的观点。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。

















