1.电磁波方程
在普通物理学中,我们已经知道,积分形式的Maxwell电磁场方程组(SI制)是
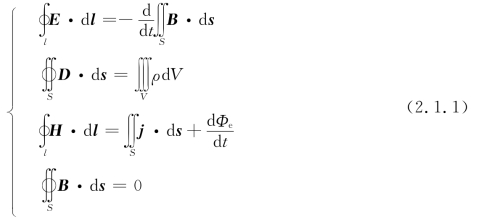
这个方程组是Maxwell在前人和他自己研究成果的基础上于1864年提出的,是经典电磁学的理论总结,也是研究包括光波导在内的电磁现象的理论基础,具有重大的理论和实践意义。这4个方程依次是意义扩充了的Faraday电磁感应定律、电场Gauss定理、Ampere环路定理和磁场Gauss定理,其中的ρ是电荷密度,j是电流密度。方程组中几个电磁场物理量的关系式是
![]()
其中,ε0和μ0分别是真空的介电常数和磁导率,P和M分别是介质的电极化强度和磁化强度。
利用矢量分析的Stokes公式和Gauss公式
![]()
可以把积分方程组(2.1.1)依次变为微分方程组:

对于自由空间,即不存在电荷和电流的空间或均匀介质,ρ=0,j=0,式(2.1.4)变为

在真空中,D=ε0E,B=μ0H,由式(2.1.5)中第一、第三两式得
![]()
上式左边
![]()
其中用到了公式a×(b×c)=b(a·c)-(a·b)c和式(2.1.5)的第二式。所以
![]()
令
![]()
得
![]()
同理得
![]()
以上两式称为真空中的电磁波方程,它们有下面的解:
![]()
或者写成复数形式:
![]()
其中,E0和B0是常矢量,k称为波矢,波矢的方向是波的传播方向,它的模k=![]() 称为波数。上面的解描述真空中的时变电磁场,即真空中的电磁波。由于振幅不变,按照波动理论,这个电磁波是真空中的平面电磁波。常数C=2.997 9×108m/s就是电磁波在真空中的波速,即光速,所以,光是一定频率范围的电磁波。
称为波数。上面的解描述真空中的时变电磁场,即真空中的电磁波。由于振幅不变,按照波动理论,这个电磁波是真空中的平面电磁波。常数C=2.997 9×108m/s就是电磁波在真空中的波速,即光速,所以,光是一定频率范围的电磁波。
2.时谐电磁波
下面讨论介质中的时变电磁场。当时变电磁场作用于介质时,由于介质中的电极化强度P相对电场强度E在时间上滞后,在各向同性的均匀电介质中,有
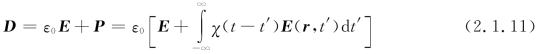
因此,瞬时关系式D(t)=εE(t)在电介质中并不成立。当然,瞬时关系式B(t)=μH(t)在电介质中也不成立。对(2.1.11)式做傅里叶变换:F [E(t)]=E(ω),利用卷积定理
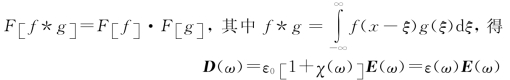
即
D(ω)=ε(ω)E(ω)
同理,有
B(ω)=μ(ω)H(ω)
所以,关系式
![]()
其中的各物理量对于各向同性均匀电介质中的时变电磁场应理解为频率的函数。ε和μ随频率变化的现象称为介质的色散。由于任何电磁波都可以用傅里叶分析法分解为不同频率电磁波的叠加,下面,我们只讨论一定频率的电磁波。
设在各向同性的均匀电介质中,电荷密度ρ=0,电流密度j=0,角频率为ω的时谐电磁波的电场和磁场分别是
![]()
将式(2.1.13)代入式(2.1.5)中,并利用式(2.1.12),得

对式(2.1.14)第一式取旋度并利用第二式,得
∇×(∇×E)=ω2μεE
由于
∇×(∇×E)=∇(∇·E)-∇2E=-∇2E
得
![]()
其中![]() 注意,式(2.1.15)满足条件∇·E=0的解才是电磁波。式(2.1.15)是一个Helmhotz方程,是一定频率的电磁波的基本方程。它的每一种满足条件∇·E=0的解称为一种模式的电磁波或电磁波的一种模式。由式(2.1.15)解出E之后,可由式(2.1.14)的第一式得到磁场:
注意,式(2.1.15)满足条件∇·E=0的解才是电磁波。式(2.1.15)是一个Helmhotz方程,是一定频率的电磁波的基本方程。它的每一种满足条件∇·E=0的解称为一种模式的电磁波或电磁波的一种模式。由式(2.1.15)解出E之后,可由式(2.1.14)的第一式得到磁场:
![]()
同理,也可得
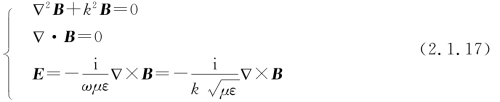
3.平面电磁波
平面电磁波是式(2.1.15)的一种最基本的解,其重要性不仅在于它体现了电磁波的基本性质,而且在于其他形式的电磁波都可以分解为各种频率的平面电磁波的叠加。如前所说,平面电磁波电场的复数表示式是
![]()
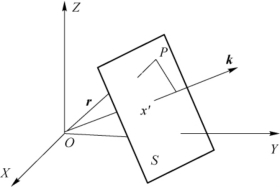
图2.1.1 波矢k方向传播的平面电磁波示意图
如图2.1.1所示,取垂直于波矢k的任一平面S,P为S上一点,其位矢为r,则k·r=kx′,x′是r在波矢k方向上的投影。由于平面S上任一点在波矢k方向上的投影都等于x′,平面S是一个等相位面。所以,式(2.1.18)描述沿k方向传播的平面电磁波。
![]()
由于∇·E=0,∇·B=0,得可见,平面电磁波的电场和磁场的方向都垂直于波的传播方向,即电磁波是横波。
将式(2.1.18)代入式(2.1.16),得
∇×E=-iωB
利用矢量分析公式:
∇×(φa)=(∇φ)×a+φ∇×a
得
![]()
式(2.1.20)表明电场与磁场相互垂直且同相,k,E,B三者的方向服从右手关系,如图2.1.2所示。由式(2.1.20)得
![]()
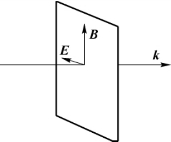
图2.1.2 k,E,B三者方向服从右手关系示意图
4.相速度和群速度
将电场强度写成式(2.1.18)的复数形式是为了便于分析。实际的电场强度是该式的实部:
E(r,t)=E0cosΦ(x,t)=E0cos(ωt-kx)
其中,k·r=kx。上式是一个无限长的等幅余弦波。设相位Φ=ωt-kx在移动中保持不变。于是,得
![]()
所以,单个波的传播速度![]() 是等相位面的移动速度,称为相速度,记作
是等相位面的移动速度,称为相速度,记作
![]()
由于μ,ε是频率的函数,不同频率的电磁波在同一介质中的速度不同,这称为介质的色散。显而易见,式(2.1.6)是式(2.1.22)在真空情形的特例。
现在考虑合成波的移动速度。不失一般性,设两个波的振幅相同,频率和波数有微小的差异,即令
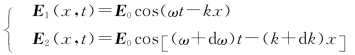
其波形如图2.1.3(a)所示,则合成波为
![]()
由于dω≪ω,dk≪k,有
![]()
其波形如图2.1.3(b)所示,是一个个的波包。显而易见,要使波包在移动中保持振幅不变,即包络上任一点A的振幅不变,必须有
tdω-xdk=常数
于是有
![]()
其中,υg称为群速度,即波包的移动速度。
在真空中,k=ω![]() ,群速度等于相速度,而在介质中,二者不相等。
,群速度等于相速度,而在介质中,二者不相等。
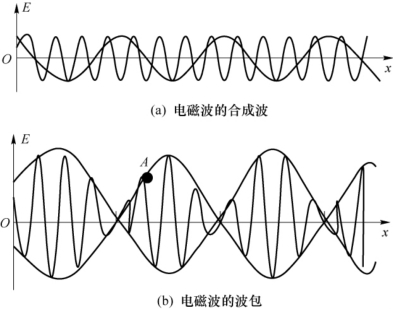
图2.1.3 电磁波的合成波与波包示意图
5.电磁波的能流密度
我们知道,电场能量密度ωe=E·D/2,磁场能量密度ωm=H·B/2,所以,电磁场能量密度:
![]()
在各向同性均匀介质中,D=εE,B=μH,电磁场能量密度可以写成:ω=![]() 真空的电磁场能量密度:
真空的电磁场能量密度:
![]()
对于真空,由式(2.1.21)得
![]()
将式(2.1.25)代入式(2.1.24),得
![]()
所以,真空中电磁波的能流密度S=Cω=EH,通常将能流密度写成矢量形式:
![]()
能流密度矢量S又称为坡印廷矢量,其方向与波矢k相同。
事实上,能量密度和能流密度的平均值更有实际意义。为便于应用,下面给出求二次式平均值的公式。设f(t)=f0e-iωt,g(t)=g0e-i(ωt-φ),则乘积fg对一个周期的平均值是
![]()
所以,能量密度和能流密度的平均值是
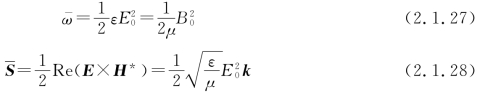
6.介质边值关系
在实际的电磁学问题中经常有不同介质的分界面,电磁场的物理量在分界面上的变化关系称为电磁量的介质边值关系。其详细叙述说明如下。
(1)法向分量的边值关系
图2.1.4所示平面S为上下两种介质的分界面。做一个扁平圆柱高斯面,使其两个底面各在一种介质内并紧贴界面。取界面法线单位矢量n的方向向上,根据式(2.1.1)第二式,当圆柱面高度趋于零时有
(D2n-D1n)ΔS=σ0·ΔS
即
![]()
σ0是界面上的自由电荷面密度,ΔS是圆柱底面面积,Dn是电位移沿界面法线方向的分量。同理,将式(2.1.1)第四式应用于图2.1.4的圆柱面,得
![]()
(2)切向分量的边值关系
如图2.1.5所示,在两种介质的界面上下做一个矩形,使其短边垂直于界面而两个长边分别在两种介质内。对此矩形环路应用式(2.1.1)第一式,设矩形长边为l,而令短边趋于零,则积分∬B·ds→0,于是有E2tl-E1tl=0,即
![]()
Et是电场强度沿界面切线的分量。
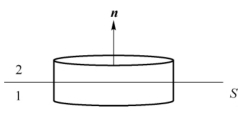
图2.1.4 电位移沿界面的法向分量示意图
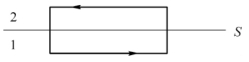
图2.1.5 电位移沿界面的切向分量示意图
同理,将式(2.1.1)第三式应用于图2.1.5的矩形回路,得
![]()
j是界面上穿过矩形所围面积的传导电流面密度。以上4个式子称为电磁场量介质边值关系,适用于连续分布介质的界面。这4个边值关系式可以写成矢量形式:

不难看出,若前两个式子成立,则后两个式子自然成立。由于在绝缘介质分界面上,j=0,σ=0,故有
![]()
和
![]()
7.电磁波在介质界面上的反射和折射
(1)反射和折射定律
波在两种介质分界面上的反射和折射源于波的基本物理量在界面上的性质。如图2.1.6所示,各向同性的均匀介质1和介质2的分界面为无限大平面S,一束平面电磁波从介质1射到界面S上发生反射和折射,假设反射波和折射波也是平面波,入射波、反射波和折射波的电场表示式分别是
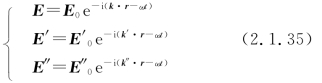
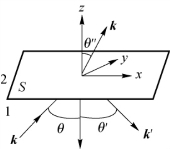
图2.1.6 电磁波在介质面上的反射和折射示意图
先来求波矢之间的关系。由于介质1中的电场是入射波和反射波的叠加,而介质2中的电场只是折射波,根据边界条件式(2.1.34)的第一式,有
n×(E+E′)=n×E″
将式(2.1.35)代入上式,得
n×(E0e-ik·r+E′0e-ik′·r)=n×E″0e-ik″·r
上式对整个界面成立。若取界面为z=0的平面,则上式对任意的(x,y)成立,因此,作为x,y的系数,波矢的各分量应分别相等:
![]()
如图2.1.6所示,设入射波波矢在xz平面内,则ky=0,即k′y=k″y=0。所以,反射波和折射波的波矢也在入射面xz平面内。设入射角、反射角和折射角分别是θ,θ′和θ″,则
![]()
由式(2.1.22)可知:
![]()
其中,υ1,υ2是两种介质中的波速。将以上两式代入式(2.1.36),得
![]()
这就是波的反射和折射定律,其中n21是介质2相对于介质1的折射率。对于非铁磁质,μ≈μ0,故近似有n21≈![]() 。由于ε=ε(ω),频率不同的电磁波介质折射率不同。
。由于ε=ε(ω),频率不同的电磁波介质折射率不同。
(2)振幅的关系
现在来考虑入射波、反射波和折射波振幅的关系。由于与一个波矢k对应的有两个独立偏振波,应分别讨论E垂直于入射面和平行于入射面两种情形。
如图2.1.7(a)所示,E垂直于入射面,由边值关系式(2.1.33)得
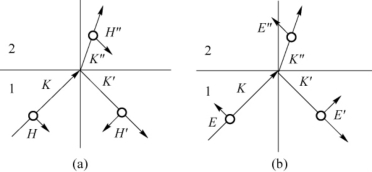
图2.1.7 E垂直于入射面与平行于入射面的示意图
![]()
Hcosθ-H′cosθ′=H″cosθ″
由式(2.1.21)得H=![]() E,取μ=μ0,可将式(2.1.40)写成
E,取μ=μ0,可将式(2.1.40)写成
![]()
利用折射定律式(2.1.39),由上式和式(2.1.40)得
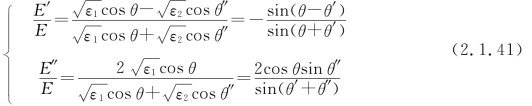
如图2.1.7(b)所示,E平行于入射面,由边值关系式(2.1.34)得
![]()
H+H′=H″
利用H=![]() E,将上式改写为
E,将上式改写为
![]()
利用折射定律式(2.1.39),由上式和式(2.1.42)得
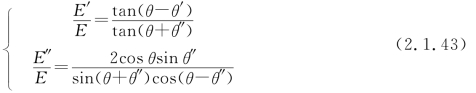
式(2.1.41)和式(2.1.43)称为Fresnel公式。这两式说明,E垂直于入射面和E平行于入射面两种偏振波的反射和折射行为不同。当入射波为自然光时,经过反射和折射后,由于两种偏振波的反射和折射波的强度不同,反射波和折射波都变为部分偏振光。当θ+θ″=90°时,按照式(2.1.43),E平行于入射面的偏振波没有反射波,于是,反射光是E垂直于入射面的完全偏振光。这就是波动光学的Brewster定律。
(3)全反射
设ε2<ε1,由![]() 可知,折射角大于入射角。这时,如果入射角使sinθ=n21=
可知,折射角大于入射角。这时,如果入射角使sinθ=n21=![]() ,折射角θ″等于
,折射角θ″等于![]() ,折射波沿界面掠过。下面来研究入射角继续增大时电磁波的传播及其物理意义。
,折射波沿界面掠过。下面来研究入射角继续增大时电磁波的传播及其物理意义。
设当sinθ≥n21时,在图2.1.6的两种介质中式(2.1.36)仍然成立,即有
![]()
于是
![]()
是一个纯虚数。令![]() 则折射波电场为
则折射波电场为
![]()
不难看出,式(2.1.45)也是Helmhotz方程式(2.1.15)的解,但由于z→-∞时,E″→∞,这个解只存在于z>0的半空间中,事实上是在z轴方向上指数衰减。所以,上式的电磁波只存在于介质2内界面附近的薄层内。薄层厚度的数量级为
![]()
现在来求折射波平均能流密度。折射波磁场强度可由式(2.1.20)得到。例如,在E″垂直于入射面时E″=E″y,有
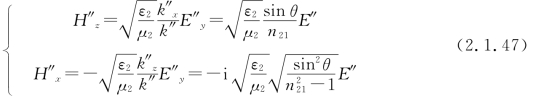
折射波平均能流密度
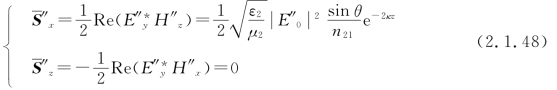
可见,折射波平均能流密度只有x分量而无z分量。
当sinθ≥n21时,反射和折射定律在形式上仍然成立,只要做变换
![]()
就可由式(2.1.41)和式(2.1.43)得到反射波和折射波的振幅和相位。例如,在E垂直于入射面时,由式(2.1.41)得
![]()
其中,tanφ=![]() 。可见,反射波和入射波振幅相同而不同相,即二者的平均能流密度相等,也就是说,当sinθ≥n21时,入射的电磁能量被全部反射。这种现象称为全反射。不过,由于反射波和入射波不同相,二者的瞬时能流密度不相等。所以,在全反射过程的前半周期内,电磁能量透入第二介质,在界面附近的薄层内储存起来,在后半周期内作为反射波能量释放出来。
。可见,反射波和入射波振幅相同而不同相,即二者的平均能流密度相等,也就是说,当sinθ≥n21时,入射的电磁能量被全部反射。这种现象称为全反射。不过,由于反射波和入射波不同相,二者的瞬时能流密度不相等。所以,在全反射过程的前半周期内,电磁能量透入第二介质,在界面附近的薄层内储存起来,在后半周期内作为反射波能量释放出来。
8.谱线的自然宽度
我们知道,原子内的电子在两能级之间跃迁时发射一条光谱线。光谱线并不是完全单色的,即光频率不是绝对不变的,而是有一定的频率分布宽度。下面应用经典振子作为原子辐射模型来说明谱线宽度的形成。
设有一个质量为m的经典振子,振动轴为x轴,弹性恢复力为-kx。当振子振动时,辐射出一定频率的电磁波,其能量要减少,相当于受到一个阻尼Fs。于是,振子的运动方程是:m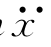 +kx=Fs。
+kx=Fs。
根据经典力学,这个阻尼可以表示为Fs=-mγ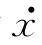 ,其中的γ称为阻尼系数。令
,其中的γ称为阻尼系数。令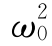 =k/m,得
=k/m,得
![]()
设式(2.1.50)有形如x=x0eiωt的解,代入式(2.1.50),得
![]()
当γ≪ω0时,解得
![]()
于是,方程(2.1.50)的解是
![]()
这是一个振幅衰减的振子。振子能量衰减到初值的e-1倍时的时间称为振子的寿命,记作τ。注意到振子能量与振幅平方成正比,得
![]()
由于振幅衰减,振子辐射的电磁波不断减弱。设振子于某时刻开始辐射,则在某空间点处观察到的电场强度是
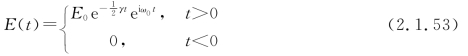
t=0是电磁波最初传到该处的时刻。式(2.1.53)不是正弦波,可分解为不同频率正弦波的叠加。对式(2.1.53)做傅里叶变换,得
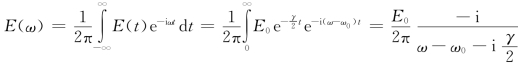
单位频率间隔的辐射能量正比于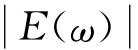 2,即有
2,即有
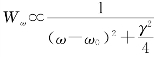
设总辐射能量为W,积分上式,得

其中,利用了积分公式![]() 。式(2.1.54)的函数曲线如图2.1.8所示。当ω=ω0时,Wω有极大值;当
。式(2.1.54)的函数曲线如图2.1.8所示。当ω=ω0时,Wω有极大值;当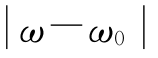 =
=![]() 时,W降为极大值的一半。因此,γ称为谱线宽度,ω它等于振子寿命的倒数。谱线宽度可用波长表示为
时,W降为极大值的一半。因此,γ称为谱线宽度,ω它等于振子寿命的倒数。谱线宽度可用波长表示为
![]()
这表明用经典振子作为原子辐射模型时,得到的谱线宽度是一个常数。事实上,原子辐射的谱线宽度变化很大,有些接近于经典谱线宽度,有些远小于经典谱线宽度。所以,谱线宽度的形成不能用经典理论完全说明,必须用量子理论来说明。不过,辐射阻尼,寿命和宽度的关系是有普遍意义的,关系式τ=1/γ依然成立。
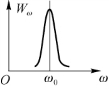
图2.1.8 总辐射能量的函数曲线示意图
9.介质的复折射率
当电磁波入射到介质中时,电子散射的次波相互叠加,形成了介质内的电磁波。介质内的宏观电磁现象取决于极化强度P和磁化强度M。对于非铁磁质,磁化强度很弱,只需考虑极化强度P与入射电磁波电场强度E的关系。为简便起见,设介质为稀薄气体。
设介质单位体积中的电子数为n,每个电子的固有振动频率为ω0。在稀薄气体中,可忽略分子间的相互作用,认为作用在电子上的电场等于入射电场。设入射电场强度为E=E0eiωt。
在入射电场作用下,电子振子的运动方程是
![]()
设上式有形如x=x0eiωt的解,代入上式,经过计算,得
![]()
所以,介质电极化强度是
![]()
利用关系式P=χeε0E和ε=εrε0=(1+χe)ε0,得电容率
![]()
可见,电容率是一个复数。相对电容率的实部是
![]()
虚部是
![]()
以上只考虑了电子的一个固有频率ω0。实际上,介质内的电子有多个固有频率。设单位体积内固有频率为ωi的电子有nfi,![]() fi=1,式(2.1.56)应改写为
fi=1,式(2.1.56)应改写为
![]()
据此,介质的折射率应为复数:
![]()
注意到在非铁质介质中![]() 是真空中的波矢,于是有
是真空中的波矢,于是有
![]()
这说明复折射率的实部引起色散,虚部引起电磁波的吸收。
需要指出的是,用量子力学可得到与式(2.1.57)类似的结果,但几率fi的意义不同,且![]() fi≠1。其次,经典理论不能算出固有频率ωi。这说明物质的宏观电磁性质的研究应当从量子力学出发。
fi≠1。其次,经典理论不能算出固有频率ωi。这说明物质的宏观电磁性质的研究应当从量子力学出发。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。














