列车在曲线上行驶会产生离心力,所以铁路在曲线段上要用外轨超高的方法来克服离心力,如图7-11所示,作用在火车上的力有两个:火车的自重P、轨道对火车的托力Q。它们的合力F便是火车得到的平衡离心力的向心力。为了使列车预期倾斜,可以通过升高外轨来达到目的,称为超高(h0) 。在图中由相似三角形的关系,有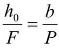 ,其中b为轨距,取值1.5m。从力学知识可知,F=mv2/R, P=mg。故
,其中b为轨距,取值1.5m。从力学知识可知,F=mv2/R, P=mg。故
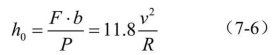
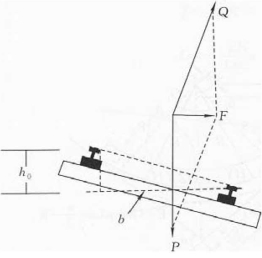
图7-11 离心力引起的外轨超高
式中,R为圆曲线半径,m;v为通过曲线的列车平均速度,km/h; g为重力加速度,9.8m/s2。
直线的曲率半径为无穷大,故列车在直线上行驶,两轨面等高。当列车进入半径为R的曲线轨道时,外轨必须突然抬高h0(当车速大、半径小时,h0的数值比较大,有时能达到10cm以上)。这种台阶状的轨面将给火车的安全运行及铁道的使用寿命带来不良的影响。解决的方法是,在直线与圆曲线之间插入一条半径由无穷大渐变至圆曲线半径R的过渡曲线(称为缓和曲线),此时超高值由0逐渐递增到h0。当半径很大,车速较低,超高h0不会很大时,对非国家等级的铁路,就不一定要增设过渡曲线。
一、缓和曲线的特性
缓和曲线可用螺旋线、三次抛物线等空间曲线形式,我国铁路上采用螺旋线。当在直线与圆曲线之间嵌入缓和曲线后,其曲率半径由无穷大(与直线连接处)逐渐变化到圆曲线的半径R(与圆曲线连接处)。螺旋线具有的特性是:曲线上任意一点的曲率半径R′与该点至起点的曲线长l成反比,即

式中,c为常数,称为曲线半径变化率。当l等于所采用的缓和曲线长度l0时,缓和曲线的半径R′等于圆曲线半径R,故
![]()
缓和曲线除了用以连接直线和圆曲线外,在复曲线测设中,当两相邻圆曲线的曲率半径差超过一定值时,这两个圆曲线必须通过缓和曲线来连接。此时,该缓和曲线的半径由第一圆曲线的R1逐渐变为第二圆曲线的R2(设R1 >R2 ) ,其曲线半径变化率c为:

式中,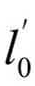 为连接两圆曲线的缓和曲线长度。
为连接两圆曲线的缓和曲线长度。
二、有缓和曲线的圆曲线要素及里程计算
图7-12 (a)为单圆曲线的情形。在直线与圆曲线间嵌入缓和曲线后,圆曲线应内移一段距离,方能使缓和曲线与直线、圆曲线衔接。而内移圆曲线,可采用移动圆心或缩短半径的办法实现,我国在铁路、公路的曲线测设中,一般采用内移圆心的方法。如图7-12(b) ,若圆曲线的圆心O1沿着圆心角的平分线内移至O(2此时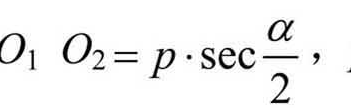 p值的大小按式
p值的大小按式
7-16计算),圆曲线的两端就可以插入缓和曲线,把圆曲线与直线平顺地连接起来。
图7-12 圆曲线的两端加入缓和曲线
具有缓和曲线的圆曲线,其主要点包括: (1) ZH点(直缓点):直线与缓和曲线的连接点; (2) HY点(缓圆点):缓和曲线和圆曲线的连接点; (3) QZ点(曲中点):曲线的中点; (4) YH点(圆缓点):圆曲线和缓和曲线的连接点; (5) HZ点(缓直点):缓和曲线与直线的连接点。
从图7-12 (b)可以看出,加入缓和曲线后,其曲线要素可以用下列公式求得:
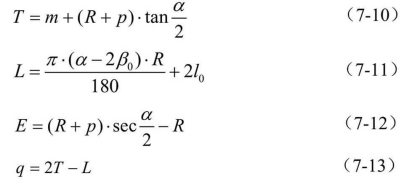
式中,α为偏角(线路转向角),R为圆曲线半径,l0为缓和曲线长度,m为加设缓和曲线后使切线增长的距离,p为加设缓和曲线后圆曲线相对于切线的内移量,β0为HY点(或YH点)的缓和曲线角度。m、 p、 β0称为缓和曲线参数,可按下式计算
![]()

从图7-12及以上公式可以看出,在圆曲线与直线之间插入长度为l0的缓和曲线后,原圆曲线及直线的一部分,被缓和曲线代替。
主要点的里程可自JD的里程算得: (1) ZH点的里程=JD的里程-T; (2) HY点的里程=ZH的里程+l0; (3) QZ点的里程=ZH的里程+L/2; (4) HZ点的里程=ZH的里程+L=JD的里程+T-q; (5) YH点的里程=HZ的里程-l0。
三、有缓和曲线的圆曲线参数方程
有缓和曲线的圆曲线,一般分为缓和曲线及圆曲线两部分讨论。
(一)缓和曲线参数方程
如图7-13所示,建立以直缓点ZH为原点,过ZH的缓和曲线切线为x轴,ZH点上缓和曲线的半径为y轴的直角坐标系。从图中不难看出,缓和曲线上任一微分线段dl与对应的dx、dy之间将有下列关系:
dx = dl·cosβ
dy = dl ·sin β
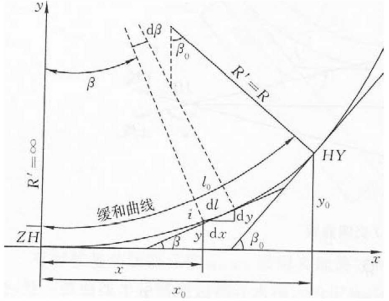
图7-13 缓和曲线坐标系
缓和曲线上任一点的坐标,可由上式取定积分求得
式中,β为l的函数。对于dl与dβ而言,根据弧长与半径的关系有![]() ,故
,故
对上式两边取定积分,得

代入前式得


代入式(7-18、 7-19)并进行定积分得
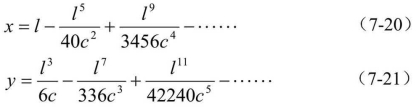
式中,c=R×l0, l为所求点到ZH点的缓和曲线长度。
实际上应用上式时,一般情况下可只取前一、二项即可,当R比较小、l0比较大时或放样精度要求高时,应加上第三项。
缓和曲线上某点的切线与ZH点切线的夹角为:

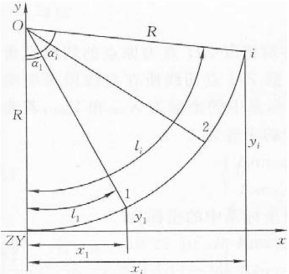
图7-14 单圆曲线坐标系
(二)圆曲线参数方程
1.单圆曲线的参数方程
对于单圆曲线(如图7-14所示),以曲线起点ZY(或终点YZ)为坐标原点,其切线为x轴,过ZY(或YZ)的半径为y轴建立直角坐标系。由图7-14中可以看出,圆曲线上任一点i的坐标为:
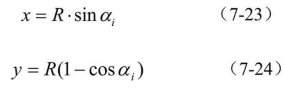
以![]() 代入上式并用级数展开,可得以曲线长li为参数的圆曲线参数方程式
代入上式并用级数展开,可得以曲线长li为参数的圆曲线参数方程式
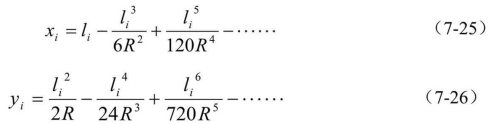
式中,li为点i到ZY(或YZ)的曲线长。
2.有缓和曲线的圆曲线的参数方程
对于两端设置缓和曲线的圆曲线而言,如图7-15所示,仍用以直缓点ZH为原点,过ZH的缓和曲线切线为x轴,半径为y轴的直角坐标系。圆曲线上的任意一点i,其到ZH点的曲线长为li。从图中看出,i点的坐标为:
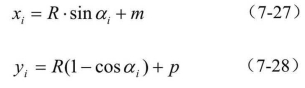
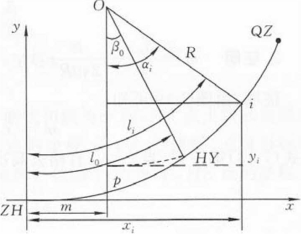
图7-15 带缓和曲线的圆曲线坐标系
式中,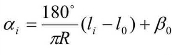 ,β0、 m、 p为前述的缓和曲线参数。
,β0、 m、 p为前述的缓和曲线参数。
若将αi以弧度表示,则![]() ,将其代入式(7-27) 、 (7-28) ,并用级数展开略去高次项,化简后即得到以li为参数的有缓和曲线的圆曲线方程式
,将其代入式(7-27) 、 (7-28) ,并用级数展开略去高次项,化简后即得到以li为参数的有缓和曲线的圆曲线方程式
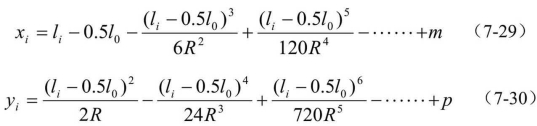
该圆曲线上任意一点i的切线与ZH点切线的夹角为:

(三)缓和曲线参数的证明
现在我们用缓和曲线方程式来证明式(7-14、 7-15、 7-16)。
1.证明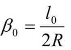
证明:由式(7-17)可知,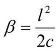 ,当时,顾及c=R·l0,即得
,当时,顾及c=R·l0,即得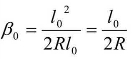
2.证明![]()
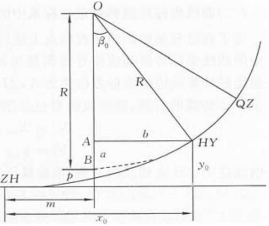
图7-16 缓和曲线参数
证明:由图7-16可知:m=x0 -b=x0-R·sinβ0 。
由式(7-22) ,当l=l0时,且略去高次项有: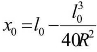 ,于是可得:
,于是可得: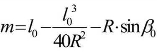
以![]() 代入,并对
代入,并对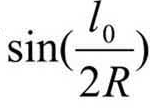
进行级数展开,取前两项整理后即得![]()
3.证明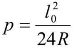
证明:由图7-16可以看出:p=y0-a=y0-R(1-cosβ0)
与求证m时同法,利用式(7-23)求得y0的表达式以及![]() 的级数展开式一同代入上式,经整理即得
的级数展开式一同代入上式,经整理即得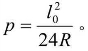
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。















